Решение задач ЛП не обладающих очевидным начальным базисом двухэтапным симплекс-методом
Задача 4. Предприятие может производить 3 вида продукции 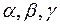 . Для их производства используются 2 вида ресурсов А и В, запасы которых
. Для их производства используются 2 вида ресурсов А и В, запасы которых 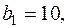
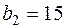 . Прибыль от реализации единицы продукции
. Прибыль от реализации единицы продукции 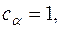
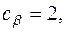
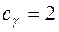 .
.
Технологическая матрица имеет вид:
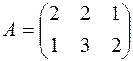 .
.
Рынок показывает, что продукт 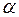 должен производиться в объеме не менее 5 единиц.
должен производиться в объеме не менее 5 единиц.
Требуется найти оптимальный план производства 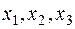 , при котором выполняются все ограничения и прибыль
, при котором выполняются все ограничения и прибыль 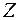 максимальна.
максимальна.
Получаем задачу ЛП:
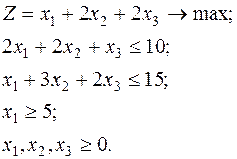 (1)
(1)
Приведем (1) к каноническому виду, вводя остаточные переменные:
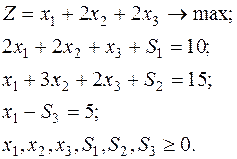 (2)
(2)
Выписывает расширенную матрицу ограничений для (2):
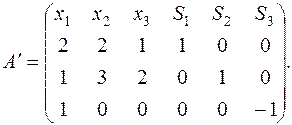
Т.к. в матрице 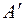 нет столбца вида
нет столбца вида 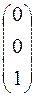 матрице
матрице 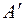 нет, поэтому в 3-ем ограничении отсутствует очевидная базисная переменная и данная задача не имеет очевидного базиса.
нет, поэтому в 3-ем ограничении отсутствует очевидная базисная переменная и данная задача не имеет очевидного базиса.
Первый этап. На первом этапе решается вспомогательная 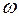 - задача, целью решения которой является нахождение начального базиса
- задача, целью решения которой является нахождение начального базиса 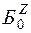 основной
основной 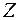 - задачи.
- задачи.
Вводим ряд искусственных переменных 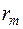 , количество которых равно количеству недостающих базисных переменных и рассматриваем новую целевую функцию:
, количество которых равно количеству недостающих базисных переменных и рассматриваем новую целевую функцию: 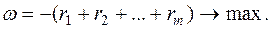
Математическая модель задачи:
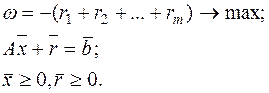 (3),
(3),
где 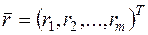 – вектор искусственных переменных.
– вектор искусственных переменных.
Вводим в 3-е ограничение вводим искусственную переменную 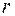 и решаем задачу вида:
и решаем задачу вида:
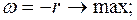
при ограничениях:
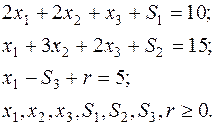 (4)
(4)
Выписываем расширенную матрицу ограничений для (4):
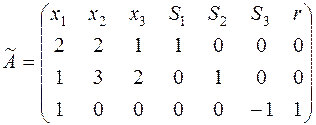
Так как в матрице 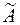 есть единичная подматрица, образованная столбцами при переменных
есть единичная подматрица, образованная столбцами при переменных 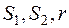 , следовательно
, следовательно 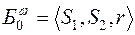 - очевидный начальный базис для
- очевидный начальный базис для 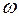 - задачи.
- задачи.
Выражаем базисную переменную 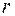 из ограничения и исключаем из целевой функции:
из ограничения и исключаем из целевой функции: 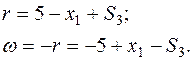
Переносим неизвестные влево:
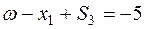 - w - строка начальной симплекс-таблицы.
- w - строка начальной симплекс-таблицы.
Строим начальную симплекс-таблицу (таблица 5) w - задачи и доводим ее до оптимальной.
Таблица 5
| Б | ω | x1 | x2 | x3 | S1 | S2 | S3 | r | Реш. | bi/ai | Комм. |
| ω | -1 | -5 | - | не опт. | |||||||
| S1 | х1→Б | ||||||||||
| S2 | Б→r | ||||||||||
| r | -1 | ||||||||||
| w | - | опт. | |||||||||
| S1 | -2 | - | |||||||||
| S2 | -1 | - | |||||||||
| X1 | -1 | - |
Т.к. 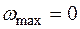 , значит, I этап завершен успешно, и искусственная переменная
, значит, I этап завершен успешно, и искусственная переменная 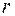 выведена из базиса.
выведена из базиса.
Второй этап .На II этапе в качестве начального базиса основной задачи принимаем оптимальный базис вспомогательной задачи, т.е. 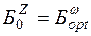 .Возвращаемся к целевой функции
.Возвращаемся к целевой функции 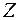 исходной задачи, и столбцы искусственных переменных
исходной задачи, и столбцы искусственных переменных 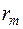 удаляем из симплекс-таблицы.
удаляем из симплекс-таблицы.
Выражаем базисную переменную 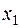 из оптимальной симплекс- таблицы и исключаем из целевой функции
из оптимальной симплекс- таблицы и исключаем из целевой функции 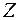 :
:
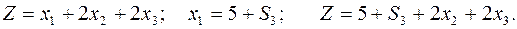
Переносим неизвестные влево: 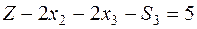 –
– 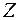 - строка начальной симплекс-таблицы основной задачи.
- строка начальной симплекс-таблицы основной задачи.
Строим начальную симплекс-таблицу основной задачи и доводим ее до оптимальной (таблица 6).
Таблица 6
| Б | Z | x1 | x2 | x3 | S1 | S2 | S3 | Реш. | bi/ai | Ком. |
| Z | -2 | -2 | -1 | - | Не опт. | |||||
| S1 | x3→Б | |||||||||
| S2 | Б→S1 | |||||||||
| x1 | -1 | - | ||||||||
| Z | - | Опт. | ||||||||
| x3 | - | |||||||||
| S2 | -1 | -2 | -3 | - | ||||||
| x1 | -1 | - |
Имеем:
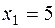 – объем производства I – го продукта.
– объем производства I – го продукта.
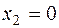 – II продукт не производится.
– II продукт не производится.
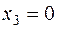 – III продукт не производится.
– III продукт не производится.
S1 = 0 – ресурс А используется полностью.
S2 = 10 – остаток ресурса В.
S3 = 0 – превышение производства продукта 1 над плановым заданием.
Замечание 4. Если 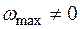 , тогда исходная задача несовместима; переход ко 2-му этапу не осуществляется;
, тогда исходная задача несовместима; переход ко 2-му этапу не осуществляется;
Экономическая интерпретация алгоритма симплекс-метода и оптимальной симплекс-таблицы
Задача 5. Предприятие может выпускать 3 различных вида продукции, цены реализации которых равны соответственно 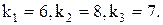 При производстве используются два вида ресурсов запасы, которых
При производстве используются два вида ресурсов запасы, которых 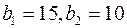 , а цены закупки единицы ресурса
, а цены закупки единицы ресурса 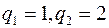 .
.
Технологическая матрица имеет вид:
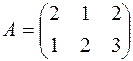 .
.
Определить оптимальный план работы предприятия, дать экономический анализ для каждой итераций поиска решения с помощью симплекс-метода.
Решение.
Пусть 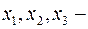 искомые объемы производства продуктов 1,2,3.
искомые объемы производства продуктов 1,2,3.
Найдем по формуле (1) ценовые коэффициенты переменных 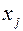 в функции прибыли.
в функции прибыли.
Имеем:
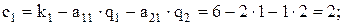
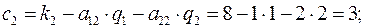
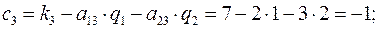
таким образом, производство продуктов 1,2 рентабельно, производство продукта 3 нерентабельно.
Задача ЛП о нахождении оптимального плана имеет вид:
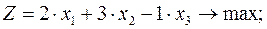
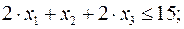
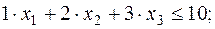
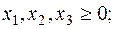
Приведем задачу (10) к каноническому виду:
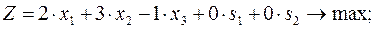
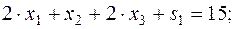
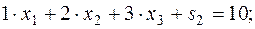
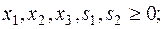
Начальный базис задачи: 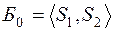 .
.
Z – строка начальной симплекс-таблицы 7:
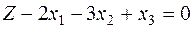 .
.
Таблица 7
| Б | Z | x1 | x2 | x3 | S1 | S2 | Реш. | bi/aij | Ком. |
| Z | -2 | -3 | - | Не опт. | |||||
| S1 | x2→Б | ||||||||
| S2 | Б→S2 |
Экономический анализ:
Производства нет: 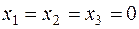 .
.
Прибыль равна 0: 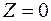 .
.
Остатки ресурсов их запасам: 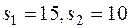 .
.
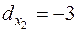 => план не оптимален, целесообразно включить в производство продукт 2, при этом прибыль составит 3руб. на 1 ед. дополнительного производства продукта 2 т.е.
=> план не оптимален, целесообразно включить в производство продукт 2, при этом прибыль составит 3руб. на 1 ед. дополнительного производства продукта 2 т.е. 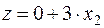 .
.
При увеличении 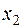 остатки ресурсов уменьшаются:
остатки ресурсов уменьшаются:
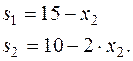
Максимально возможный объём производства продукта. 2:
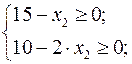 →
→ 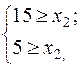 →
→ 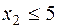 →
→ 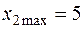 .
.
Следовательно, производство продукта 2 можно увеличить до 5 ед. При этом ресурс 2 расходуется полностью: 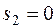 , а остаток ресурса составит:
, а остаток ресурса составит: 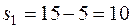 ед. Новый план производства представлен в таблице 8.
ед. Новый план производства представлен в таблице 8.
Таблица 8
| Б | Z | x1 | x2 | x3 | S1 | S2 | Реш. | bi/aij | Ком. |
| Z | -1/2 | 11/2 | 3/2 | - | Не опт. | ||||
| S1 | 3/2 | 1/2 | -1/2 | 20/3 | x2→Б | ||||
| x2 | 1/2 | 3/2 | 1/2 | Б→S2 |
Экономический анализ:
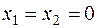 - продукты 1 и 3 не производятся,
- продукты 1 и 3 не производятся,
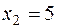 - объём производства продукта 2;
- объём производства продукта 2;
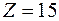 - размер получаемой прибыли.
- размер получаемой прибыли.
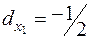 => план не оптимален; целесообразно увеличивать производство продукта 1, при этом прибыль увеличивается на 0.5 руб. на 1 ед. увеличения производства продукта 1, т.е.
=> план не оптимален; целесообразно увеличивать производство продукта 1, при этом прибыль увеличивается на 0.5 руб. на 1 ед. увеличения производства продукта 1, т.е. 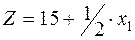 .
.
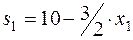 , остаток ресурса 1 идет на производство продукта 1.
, остаток ресурса 1 идет на производство продукта 1.
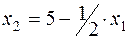 - производство продукта 2 уменьшается, т.к. необходимо освободить часть ресурса 2 для производства продукта 1.
- производство продукта 2 уменьшается, т.к. необходимо освободить часть ресурса 2 для производства продукта 1.
Максимально возможный объём производства продукта. 2:
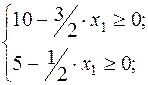 →
→ 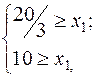 →
→ 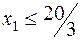 →
→ 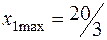 .
.
Следовательно, производство продукта 1 можно увеличить до 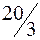 ед. При этом ресурс 1 расходуется полностью:
ед. При этом ресурс 1 расходуется полностью: 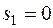 , а объём производства товара 2 уменьшится до:
, а объём производства товара 2 уменьшится до: 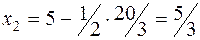 ед.
ед.
Оптимальный план производства представлен в таблице 9.
Таблица 9
| Б | Z | x1 | x2 | x3 | S1 | S2 | Реш. | bi/aij | Ком. |
| Z | 17/3 | 1/3 | 4/3 | 55/3 | - | опт. | |||
| x1 | 1/3 | 2/3 | -1/2 | 20/3 | - | ||||
| x2 | 4/3 | -1/3 | 2/3 | 5/3 | - |
Экономический анализ:
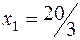 - производство продукта 1;
- производство продукта 1;
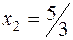 - производство продукта 2;
- производство продукта 2;
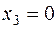 - продукт 3 не производится.
- продукт 3 не производится.
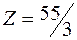 - максимальная прибыль.
- максимальная прибыль.
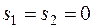 - ресурсы используются полностью.
- ресурсы используются полностью.
Экономический анализ ресурсов:
Таблица 10
| Ресурс | Отаток | Статус | Ценность | Комментарий |
| дефицит | 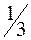
| Цена на ресурс может возрасти не более чем на 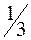 руб., но его выгодно будет использовать Закупка 1 ед. ресурса по текущей цене и включение в производство дает дополнительную прибыль руб., но его выгодно будет использовать Закупка 1 ед. ресурса по текущей цене и включение в производство дает дополнительную прибыль 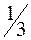 руб. руб.
| ||
| дефицит | 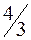
| Цена на ресурс может возрасти не, более чем на 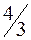 руб., но его выгодно будет использовать. Закупки 1 ед. ресурса по текущей цене и включение в производство дает дополнительную прибыль руб., но его выгодно будет использовать. Закупки 1 ед. ресурса по текущей цене и включение в производство дает дополнительную прибыль 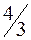 руб. руб.
|
Вывод: В первую очередь стоит приобретать ресурс 2 как более ценный.
Экономический анализ продуктов:
Таблица 11
| Продукт | Статус | Относительная оценка в опт плане | Комментарий |
| базисный | Выгодный, производится в объеме 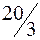 и дает вклад в прибыль и дает вклад в прибыль 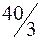 руб. руб.
| ||
| базисный | Выгодный, производится в объеме 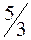 и дает вклад в прибыль и дает вклад в прибыль 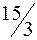 руб. руб.
| ||
| не базисный | 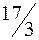
| Не производится. Убыток от производства 1 ед. продукта по сравнению с опт. планом составит 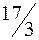 руб. Производство станет выгодным, если цена реализации увеличивается, по крайней мере, на руб. Производство станет выгодным, если цена реализации увеличивается, по крайней мере, на 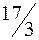 руб. руб.
|
Дата добавления: 2014-11-29; просмотров: 826;
