Автономная некоммерческая организация высшего образования

Жарық -

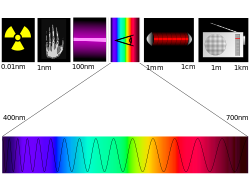
1. тар мағынада – көрінетін сәуле, яғни жиілігі 7,5 •1014 – 4,0 • 1014Гц аралығындағы адам көзі қабылдайтын электрмагниттік толқын;

2. кең мағынасында — қабылданатын сәулемен бірге спектрдің ультракүлгін және инфрақызыл аймағындағы сәулелерді де қамтитын оптикалық сәуленің синонимі.

Жарық дифракциясы – жарық толқындарының мөлшері сол толқындардың ұзындығымен қарайлас тосқауылды (тар саңылау, жіңішке сым, т.б.) орап өту құбылысы. Жарық дифракциясы болу үшін жарық түскен дененің айқын шекарасы болуы тиіс. Дифракция жарыққа ғана тән емес, басқа да толқындық процестерде де байқалады (мысалы, механикалық толқындардың жолында кездескен тосқауылды орап өтуі, т.б.). Жарық дифракциясы кезінде жарықтың түзу сызық бойымен таралу заңы, яғни геометриялық оптиканың негізгі заңдары бұзылады. Жарық толқындарының ұзындығы өте қысқа болғандықтан, қалыпты жағдайда жарық дифракциясы байқалмайды. Жарық дифракциясы – жарықтың толқындық қасиетін дәлелдейтін негізгі құбылыстардың бірі. Бұл құбылысты 17-ғасырда италиялық физик және астроном Франческо Гримальди ашты, ал оны француз физигі Огюстен Жан Френель түсіндірді.

Жарық жылдамдығы – кез келген электрмагниттік толқындардың (оның ішінде жарықтың да) бос кеңістіктегі (вакуумдағы) таралу жылдамдығы; іргелі физикалық тұрақтылардың бірі. Жарық жылдамдығының шамасы материалдық дененің массасы мен толық энергиясын байланыстырып тұрады. Санақ жүйесі өзгерген кезде координатты, жылдамдықты және уақытты түрлендіру жарық жылдамдығы арқылы өрнектеледі. Жарық жылдамдығын алғаш рет 1676 ж. Юпитер серіктерінің тұтылулары арасындағы уақыт аралығының өзгеруі бойынша дат астрономы Оле Ремер өлшеді (бақылау нәтижесінде с=215000 км/с болды). Жарық көзі ретінде лазерлерді пайдаланып жүргізген өлшеулер нәтижесінде жарық жылдамдығын өлшеу дәлдігі жоғары көтерілді: с=299792,5•0,15 км/с. Қазіргі кезде жарық жылдамдығының вакуумдағы мәні үшін ресми түрде с=299792,458•1,2 м/с қабылданған.

Жарық интерференциясы – жарық толқындарының қабаттасуы нәтижесінде бірін-бірі күшейтуі немесе әлсіретуі. Егер екі толқынның өркештері мен өркештері, сайлары мен сайлары дәл келсе, онда олар бірін-бірі күшейтеді; ал біреуінің өркештері екіншісінің сайларына дәл келсе бірін-бірі әлсіретеді. Жарық интерференциясы кезінде қабаттасқан жарық шоғының қарқындылығы бастапқы шоқтың қарқындылығына тең болмайды. Механикалық толқындар да интерференцияланады. Кез келген жарық толқындары қабаттасқанда интерференция құбылысы байқалмайды. Тек когерентті толқындар ғана интерференцияланады. Жарық интерференциясының көмегімен жарық толқындарының ұзындығы өлшенеді, спектр сызықтарының нәзік түзілісі зерттеледі, заттың тығыздығы мен сыну көрсеткіші тәрізді қасиеттері анықталады.

Жарық қысымы – жарықтың шағылдыратын немесе жұтатын денеге түсіретін қысымы. Күн маңынан ұшып өткен кезде құйрықты жұлдыздың (кометаның) құйрығының қисаюына жарық қысымының әсері болатындығын 1619 ж. алғаш рет неміс ғалымы Иоганн Кеплер болжаған. 1873 ж. ағылшын физигі Джеймс Максвелл электрмагниттік теорияға сүйене отырып, жарық қысымының шамасын анықтады. 1899 ж. орыс физигі Петр Лебедев жарықтың қатты денелерге, кейінірек газдарға (1907 – 10) түсіретін қысымын өлшеді. Жарық қысымын жарықтың электрмагниттік теориясы мен кванттық теориясы негізінде түсіндіруге болады. Жарық қысымы әсерінен Жердің жасанды серіктерінің орбиталары аз да болса толықсиды.

Жарықтың сынуы – екі ортаның шекаралық қабатына түскен сәуленің екінші ортаға өткен бөлігінің бастапқы бағыттан ауытқуы. Жарықтың сыну заңдары былай тұжырымдалады:

1. түскен сәуле, сынған сәуле және екі ортаны бөлетін шекаралық бетке жүргізілген перпендикуляр бір жазықтықта жатады. Түскен сәуле мен сынған сәуле өзара қайтымды болады;

2. түсу бұрышы синусының (α) сыну бұрышы синусына (φ) қатынасы тұрақты шама болады: мұндағы n – ортаның сыну көрсеткіші. Берілген заттың вакууммен салыстырғандағы сыну көрсеткіші сол заттың абсолюттік сыну көрсеткіші деп аталады.

Жарықтың шағылуы – жарықтың екі түрлі орта шекарасына (кем дегенде біреуі мөлдір болатын) түсуі кезінде байқалатын құбылыс. Мөлдір ортадағы жарық сәулесі сыну көрсеткіші сол ортаға қарағанда өзгеше болатын екінші ортаға жеткен соң, оның біршама бөлігі сынып, басқа бағытпен таралады да, енді бір бөлігі бірінші ортаға қарай кері шағылады. Шағылған және сынған сәулелер қарқындылығының салыстырмалы шамасы жарық түскен дене бетінің тегістігіне, жарықтың құрамы мен түсу бұрышына, т.б. байланысты болады. Кейде жарық сәулесі толығымен кері шағылады.

Жарықтың шашырауы – жарық сәулесінің бастапқы таралу бағытын өзгертіп, жан-жаққа ауытқуы. Бұл құбылыс жарықтың оптикалық жағынан біртекті емес ортада таралуы кезінде байқалады. Сол орта ішіндегі бөгде бөлшектер жарықтың таралу бағытын өзгертеді. Жарық толқынының электр өрісі әсерінен мұндай орта электрондары еріксіз тербеледі де, барлық бағытта бастапқы толқын жиілігіндей екінші реттік электрмагниттік толқындар шығарады. Жарық бөгде қоспалардан мұқият тазартылған ортадан (заттан) өткенде де шашырайды. Өйткені молекулалар мен атомдар үздіксіз қозғалыста болатындықтан, шағын көлем ішінде де заттың тығыздығы өзгеруі мүмкін. Осы өзгеріс салдарынан да жарық шашырауы байқалады.

10. Кванттық теориядағы сутегі атомы және молекуласы.Кванттық сандар– кванттық жүйелерді, жеке элементар бөлшектерді, жорамал бөлшектерді сипаттайтын физикалық шамалардың мүмкін мәндерін анықтайтын бүтін немесе бөлшек сандар. Кванттық жүйе күйін түгелдей анықтайтын кванттық сандардың жиынтығын толық кванттық сандар деп атайды. Атомдағы электронның күйі үш кеңістіктік координата және спинмен байланысқан электронның төрт еркіндік дәрежесіне сәйкес келетін төрт кванттық санмен анықталады. Олар сутек атомы және сутек тәрізді атомдар үшін былайша аталады: бас кванттық сандар (n), орбиталық кванттық сандар (l), магниттік кванттық сандар (ml), магнитті спиндік не спиндік кванттық сандар (ms). Кванттық сандар микродүниеде өтетін процестердің дискретті сипаты бар екендігін бейнелейді әрі олар әсер квантымен, яғни Планк тұрақтысымен тығыз байланысты болады. Спин-орбиталық өзара әсер ескерілген кезде электронның күйін сипаттау үшін ml мен ms-тің орнына толық қозғалыс мөлшері моментінің кванттық саны (j) мен толық момент проекциясының кванттық саны (mj) пайдаланылады. Атомның, т.б. кванттық жүйелердің күйін сипаттау үшін күй жұптылығы (P‘) делінетін тағы да бір кванттық сан енгізіледі. Ол +1 не –1 мәндерін қабылдайды. Элементар бөлшектер физикасы мен ядролық физикада бұдан да басқа кванттық сандар енгізіледі. Мысалы, электрлік заряд (Q), бариондық заряд (B), ),изотоптық m электронды-лептондық заряд(Le), мюонды-лептондық заряд (L спин (T), ғажаптылық (оғаштық) (S) не гиперзаряд, т.б. Кванттық сандар элементар бөлшектердің кванттық сандары олардың (бөлшектердің) өзара әсері мен бір-біріне айналу процесін анықтайтын ішкі сипаттамасы болып табылады. Кең мағынада кванттық сандар деп, көбінесе, кванттық механикалық бөлшектер (немесе жүйелер) қозғалысын анықтайтын және қозғалыс кезінде сақталатын физикалық шамаларды айтады. Паули принцип, тыйым салу принципі — табиғаттың іргелі заңдарының бірі. 1925 жылы швейцариялық физик В.Паули (1900 — 58) тұжырымдаған. Паули принцип бойынша кванттық жүйеде спині жартылай бүтін екі не одан да көп бірдей бөлшектер бір мезгілде бір күйде бола алмайды. Паули принцип химиялық элементтердің периодтық жүйесін, атом ядроларының, молекулалардың, кристалдардың қасиеттерін түсіндіруде маңызды рөл атқарады.

11. Сутегі атомына арналған Шредингер теңдеуі.Шредингер теңдеуі, толқындық теңдеу – релятивистік емес кванттық механиканың негізгі теңдеуі. Мұны алғаш рет Э.Шредингер тапты (1926). Ньютонның механикадағы қозғалыс теңдеулері мен Максвелл электрдинамикадағы теңдеулері классик. физикада қандай түбегейлі рөл атқарса, Шредингер теңдеуі кванттық механикада сондай рөл атқарады. Шредингер теңдеуі толқындық функция (пси функция) арқылы кванттық нысандар күйінің уақыт бойынша өзгеруін сипаттайды. Егер бастапқы кездегі толқындық функцияның мәні 0 белгілі болса, онда Шредингер теңдеуін шешу арқылы осы функцияның кез келген уақыт мезетіндегі мәнін (x, y, z, t) табуға болады. V(x, y, z, t) потенциалы тудыратын күштің әсерінен қозғалатын, массасы m бөлшек үшін Шредингер т. мына түрде жазылады: , мұндағы d2/dx2+d2/dy2+d2/dz2 Лаплас операторы, =h/2 – Планк тұрақтысы. Бұл теңдеу Шредингердің уақытқа тәуелді теңдеуі деп аталады. Егер V уақытқа тәуелсіз болса, онда Шредингер теңдеуі төмендегі түрде жазылады: , мұндағы Е-кванттық жүйенің толық энергиясы. Бұл теңдеу Шредингердің стационер күйдегі теңдеуі деп аталады. Кеңістіктің шектелген аумағында қозғалатын кванттық жүйелер (бөлшектер) үлесі Шредингер теңдеуінің шешімі энергияның кейбір дискретті (үздікті) мәндерінде n1, n2, …, nn, … ғана болады; бұл қатардың мүшелері бүтін кванттық сандармен (n) нөмірленеді. Әрбір n-нің мәніне n (x, y, z) толқындық функциясы сәйкес келеді. Толқындық функцияның толық жиынтығы n1, n2, …, n, белгілі болса, кванттық жүйенің барлық параметрлерін анықтауға болады. Шредингер теңдеуі табиғаттағы микробөлшектердің бөлшектік-толқындық қасиеттерін матем. өрнек арқылы толық сипаттайды және ол сәйкестік принциптерін қанағаттандырады. Бұл теңдеу шекті жағдайда (де Бройль толқынының ұзындығы қарастырылып отырған қозғалыстың өлшемдерінен әжептәуір кіші болғанда) бөлшектердің қозғалысын классик. механика заңдарымен сипаттауға мүмкіндік береді. Шредингер теңдеуінен қозғалысты траектория арқылы сипаттайтын классик. механика теңдеулеріне ауысу толқындық оптикадан геометрик. оптикаға ауысуға ұқсас. Матем. көзқарас бойынша Шредингер теңдеуі толқындық теңдеуге жатады және өзінің құрылымы бойынша периодты әсер ететін жіңішке ішектің тербелісін сипаттайтын теңдеуге ұқсас. Бірақ ішектің тербелісін сипаттайтын теңдеудің шешімі берілген уақыт мерзіміндегі ішектің геометр. пішінін беретін болса, ал Шредингер теңдеуі шешімінің тікелей физикалық мағынасы болмайды. Дегенмен толқындық функция квадратының n(x, y, z, t)/2 физикалық мағынасы бар. Ол бөлшектің температурасы ӘС уақыт мезетіндегі координаттары x, y, z, нүктенің төңірегінде бірлік көлемде болу ықтималдылығын анықтайды. Ықтималдықтарды қосу теоремасына сүйеніп микробөлшекті температурасы ӘС уақыт кезеңінде шекті V көлемде мына өрнек арқылы табуға болады: мұндағы W – микробөлшектің V көлемде орналасу ықтималдылығы.

12. Кемтіктік өткізгіштер түсінігі. Кемтiктердiң қозғалысы- бұл электрондардың бiр байланыстан көршi екiншi байланысқа көшуi болып табылады. Осындай қоспалар электрон «алатынң акцепторлық қоспалар деп аталады. Кристалдағы қоспалардың мөлшерi артқанда оның өткiзгiштiгi электрондық немесе кемтiктiк сипат алады. Negativ (терiс) деген латын сөзiнiң бiрiншi әрiпiне сәйкес электрондық өткiзгiштiгi n-типтi өткiзгiштiк, positiv (оң) сөзiнiң бiрiншi әрiпiне сәйкес кемтiктiк өткiзгiштiктi p-типтi өткiзгiштiк деп аталады. Қоспалары бар жартылай өткiзгiштерде екi түрлі электр тогын тасымалдаушылар болады. Олар қоспа атомдарын енгiзу нәтижесiнде пайда болатын негiзгi электр тогын тасымалдаушылар және жылулық энергия нәтижесiнде пайда болатын негiзгi емес электр тогын тасымалдаушылар.

Техникада қолданылған алғашқы жартылай өткiзгiштiк материал селен болды. Қазiргi уақытта жиi қолданылатын материалдар кремний, германий, селен болып табылады. Бұл заттар элементар жартылай өткiзгiштерге, яғни Менделеев периодтық кестесінің элементiне жататын жартылай өткiзгiштерге жатады.

Германий, кремний және селенмен қатар қазiргi кезде Менделеев таблицасындағы ІІІ және V, ІІ және ІV, ІІ және VІ топтардың элементтерiнен алынатын күрделi жартылай өткiзгiштiк қоспалар қолданылады. Мысалы, галий мен мышьяктың (галий арсенидi), галиймен фосфор, сынап пен теллурдың қоспалары және т.б.. Жартылай өткiзгiшке енгiзетiн қоспа түрiнде бор, фосфор, индий, мышьяк, сурьма және жартылай өткiзгiшке қажеттi қасиеттер беретiн басқа да элементтер қосады.

Металл-жартылай өткiзгiш және жартылай өткiзгiш- жартылай өткiзгiш түйiсулерi Ом заңына бағынбайды. Бұл түйiсулердегi кедергi түсiрiлген кернеуге тәуелдi және кернеудiң бiрдей мәнiнде токтың бағытына байланысты өзгередi.

Жоғарыда айтылғандай жартылай өткiзгiштердiң өткiзгiштiгi сипатына байланысты электрондық (n-типтi) және кемтiктiк (p-типтi) болуы мүмкiн. n-типтi жартылай өткiзгiштерде негiзгi заряд тасымалдаушылар электрондар, ал p-типтi жартылай өткiзгiштерде кемтiктер болып табылады. Екi жартылай өткiзгiштiң түйiсуiнде электрондар мен кемтiктер бiр жартылай өткiзгiштен екiншi жартылай өткiзгiшке өте алады. Сондықтан жартылай өткiзгiштердiң арасында түйiсу потенциалдар айырмасы пайда болады да, ал жұқа шекаралық қабатта түйiсу электрлiк өрiсi пайда болады.Егер бiр типтi (екеуi де электрондық немесе екеуi де кемтiктiк) жартылай өткiзгiштер түйiссе, онда екi жартылай өткiзгiште бiрдей бөлшектермен алмасады (не кемтiктермен не электрондармен). Сондықтан түйiсетiн жартылай өткiзгiштердiң бiреуi n-типтi, екiншiсi p-типтi болған жағдайды қарастырамыз. Бұндай түйiсулер электрондық-кемтiктiк ауысу немесе p-nауысу деп аталады. Осындай түйiсулерде таза күйiнде алу мүмкiн емес. Себебi екi жартылай өткiзгiштi бiр-бiрiне түйiстiргенде беттерiнiң тегiстiк еместiгiнен түйiсу тек кейбiр нүктелерде жүредi, ал олардың арасында ауа қабаттары болады. Сондықтан p-n ауысуын алу үшiн таза жартылай өткiзгiшке (мысалы, германий, кремний) екi қоспа - бiреуi донорлық (яғни, электрондық өткiзгiштiк бередi), ал екiншiсi акцепторлық (яғни, кемтiктiк өткiзгiштiк бередi), пластинканың бiр шетiнде бiр қоспа, ал екiншi шетiнде екiншi қоспа артық болатындай түрде енгiзiледi. Сонда пластинканың бiр жартысындай электрондық өткiзгiштiк, ал екiншi жартысында кемтiктiк өткiзгiштiк пайда болады және осы екi қоспалар бiрiн- бiрi теңестiредi.

13. Меншікті және қоспалы өткізгіштер. Ең жиі қолданылатын жартылай өткізгіштер: кремний, германий, галлий арсениді, селен, теллур, әртүрлі оксидтер, сульфидтер, нитридтер және карбидтер. Егер әртүрлі элементтердің атомдарының құрылысын қарастырсақ онда электрондармен толыққан (ішкі) және толықпаған қабықшаларын (сыртқы) бөлуге болады. Соңғысы ядромен әлсіз байланыста болғандықтан басқа атомдармен оңай әсерлеседі. Сондықтанда сыртқы толықпаған қабықтағы электрондарды валентті деп атайды. Молекула құрғанда жеке атомдардың арасында әртүрлі типтегі байланыстар болады. Жартылай өткізгіштер үшін ең көп тарағаны ковалентті байланыс. Мысалы, Кремнийдің (Si) атомы төрт валенттік электронға ие, молекулаларда көршілес төрт атомның арасында ковалентті байланыс болады (сурет 1). Абсолютті таза және біртекті жартылай өткізгіште нөлден өзгеше температурада бос электрондар мен кемтіктер жұп құрады, яғни электрондар мен кемтіктердің саны тең болады. Мұндай жартылай өткізгіштің электр өткізгіштігі меншікті электр өткізгіштік деп аталады.

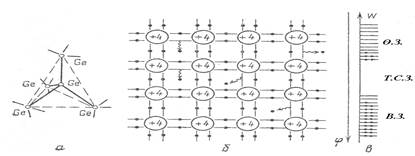
Сурет1

Таза күйінде Si және Ge диэлектриктік қасиеттерге иеленеді, бірақ олардың өткізгіштігі аз мөлшерде (шамада) қоспаларды енгізсе түпкілікті өзгереді. 2 суретте Ge-дің (кристалл торының) моделі, оның бір атомын As (күшән) атомымен орынбастырылған. Міне осы As-атомды қоспа дейді. Күшәннің (As-тің) сыртқы орбитасында 5 электрон, сондықтан Ge-кристалына «тұрғанда» оның бір электроны еркін болып қалады.
Бұл артық электрон өте қозғалғыш, сондықтан потенциалдар айырымы пайда болғанда ток тасымалдаушы бола алады. Еркін электрондар санын (мөлшерін) жартылай өткізгіш ішіне енгізілетін қоспа атомдар санын өзгертіп бақылауға (тексеруге) болады. Қоспаларды жартылай өткізгіштерге енгізгенде еркін электрондар пайда болса – бұл жартылай өткізгіш енгізілген қоспа донор деп аталады, ал жартылый өткізгішінің өзі қоспалы жартылай өткізгіш деп аталады.

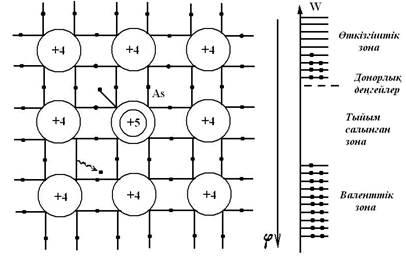
Сурет2
Донор қоспасы бар жартылай өткізгіштерде өткізгіштік еркін электрондармен сипатталады да, бұндай жартылай өткізгіштерді n-типті (negative) деп атайды.

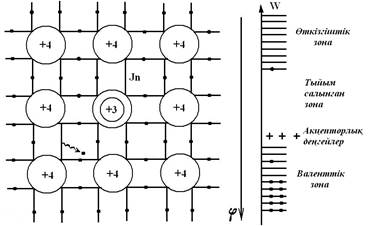
Сурет3
Егер жартылай өткізгіш – кристалл торы ішіне сыртқы қабаттарыда үш электрон болатын, мысалы Бор, Индий атомдарын енгізетін болсақ, электронның жоқтығы кристалл ішінде кемтіктің пайда болуына келтіреді (сурет 3). Сырттан түсірілген кернеу бұндай жартылай өткізгіштерде электрондардың оң таңбалы түйіспеге , ал кемтіктердің теріс таңбалы түйіспе жағына қозғалысына келтіріледі. Кемтіктердің қозғалысын да ток ретінде қарастыруға болады. Жартылай өткізгіштерді р-типті (positive) деп, ал қоспаларды акцепторлар деп атауға келіскен. Жоғарыда қарастырылған негізгі заряд тасушылармен қатар (бұлар жартылай өткізгіш ішіне қоспаларды қосқанда пайда болады дедік) кәдімгі қыздыру әрекетінен пайда болатын еркін электрондар (оларды негізгі емес заряд тасушылар деп атайды) да токқа үлесін қосады.

13. Атом ядросы —протондар мен нейтрондардан (нуклондардан) құралатын атомның ең ауыр, орталық бөлігі.

Атом ядросының негізгі сипаттамаларының бірі оның электр заряды болып табылады. Атом ядросының зарядын алғаш рет 1913 жылы Г.Мозли өлшеген. Ал ядроның зарядын тікелей өлшеуді ағылшын физигі Дж.Чедвик 1920 жылы жүзеге асырды. Атом ядросының заряды элементар электр зарядының Менделеев кестесіндегі химиялық элементтің 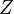реттік нөміріне көбейтіндісіне тең болады:

.

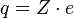Сонымен, Менделеев кестесіндегі химиялық элементтің реттік нөмірі кез келген элемент атомының ядросындағы оң зарядтардың санымен анықталады. Сондықтан элементтің 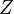реттік нөмірін зарядтық caн деп атайды.

Атом ядросының физикалық қасиеттері оның зарядымен қатар массасымен де анықталады. Ядроны сипаттайтын шамалардың ең маңыздыларының бірі — масса. Ядролық физика иондар мен атом ядросының массасын көбінесе масс-спектрографтың көмегімен анықтайды. 8.2-суретте масс-спектрографтың сұлбасы келтірілген. Зерттелетін заттың атомдары иондық көзде (ИК) оң иондалып, әлсіз электр өрісінің әсерінен 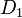диафрагма арқылы әр түрлі жылдамдықпен өтеді. 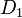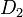және диафрагмалары арасында оң иондар электр өрісінде үдемелі қозғалады. Және осы мезетте оңиондарға индукциясы 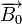болатын магнит өрісі де әсер етеді. Осылайша үдетілген оң иондар, оған бір-біріне перпендикуляр бағытталып әсер ететін 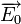электр және 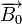магнит өрістері арқылы сұрыпталып өтеді. 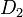диафрагма арқылы бұрылмай өтуі үшін 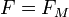немесе 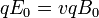шарты орындалуы керек. Бұл теңдеуден жылдамдықты анықтайық:

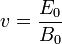
Осы жылдамдыққа ие болған оң иондар біртекті 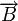магнит өрісінде орналасқан ВК вакуумдік камераға өтеді. Магнит өрісінің индукция векторы 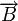иондардың жылдамдық векторына перпендикуляр орналаскан. Магнит өрісінде козғалған оң иондарға модулі 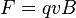болатын Лоренц күші әрекет етеді. Иондар осы күштің әрекетінен шеңбер бойымен қозғалады. Жартылай шеңбер сыза отырып, массалары бірдей иондар ФП фотопластинаның түрлі орындарында тіркеледі.

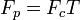немесе 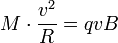болғандықтан, ионның массасын

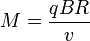
өнергі бойынша жоғары дәлдікпен анықтайды. Атом ядросының массасын 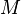әрпімен белгілеу қабылданған.^[1]

Ядролық физикадағы өлшем бірліктер[өңдеу]

Өлшем бірліктерінің Халықаралык жүйесіндегі қолданылатын ұзындықтың, массаның және т.б. өздеріңе таныс өлшем бірліктерімен қатар, ядролық физикада арнайы бірліктер қолданылады. Бұл қажеттілік ядролық процестердің субатомдық әлемде өтетінінен туындайды.

Мысалы, ядролық физикадағы ең үлкен қашықтық атом радиусының өзі 10⁻¹⁰ м-ге тең. Ұзындық бірлігі ретінде ферми алынады: 1фм = 10⁻¹⁵ м. Массаның бірлігі ретінде көміртегі 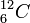атомы массасының бөлігі алынады, ол массаның атомдық бірлігі болып табылады:

1 м.а.б.=1,660546 · 10^-27 кг, 1 кг=6,023091 · 10²⁶ м.а.б.

Салыстырмалы атомдық масса

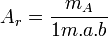
атомның абсолюттік массасында неше массаның атомдық бірлігі бар екенін көрсетеді. Мысалы, сутегі үшін A_r= 1,00783, көміртегі үшін A_r = 12,0 , оттегі үшін A_r = 15,99482.

Ядролық физикада энергияны электронвольтпен өлшейді,

1 эВ = 1,6 · 10^-19 Дж.

Еселік мәндер де қолданылады:

1 кэВ =10³ эВ; 1 МэВ =10⁶ эВ;1 ГэВ =10⁹ эВ.

Көбінесе элементар бөлшектердің массаларын массаның атомдық бірлігімен қатар энергияның өлшем бірлігі МэВ немесе ГэВ-пен де өлшейді. Сондықтан массаның атомдық бірлігіне сәйкес болатын энергияның эквивалентін анықтайық. Масса мен энергияның өзара байланыста болатыны Эйнштейннің 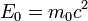формуласынан белгілі.

Атомдағы электрондар массасы ядроның массасымен салыстырғанда өте аз, оны ескермеуге болады. Сондықтан массаның атомдық бірлігімен алынған және атом массасына ең жақын бүтін санды массалық сан деп атайды. Оны 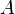әрпімен белгілейді. Ол жоғары дәлдікті қажет етпейтін есептеулерде, әсіресе массалардың қатынасы кіретін өрнектерде ядро массасының шамасы ретінде қолданылады. Мысалы, гелий атомының массасы M_He = 4,0026 м.а.б.болса, массалық саны A = 4 болады.^[1]

Атом ядросының пішіні мен өлшемі[өңдеу]

Көптеген эксперименттік зерттеулер атом ядросының пішіні сфера тәрізді болатынын көрсетті. Атом ядросының радиусын мына формула бойынша жуықтап анықтауға болады:

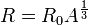
мұндағы R₀ = 1,25 = 1,25 · 10^-15 м, A — массалық сан. Ал ядроның радиусы оның массалық санының кубтық түбіріне пропорционалдығынан ядролық заттың орташа тығыздығы үшін

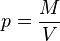
шығады, мұндағы М_я = (m_р + m_n) · А — ядроның массасы. Есептеулер жуықтап алғанда ядролық заттың орташа тығыздығы р ~ 2,7 · 10¹⁷ кг/м³ - екенін көрсетті. Заттың осындай тығыздығы ғарыштағы нейтрондық жұлдыздар-пульсарларға да тән көрінеді.

Пайдаланылған әдебиеттер:

1. абдулаев ж., асқаров п. физика курсы. -алматы: ғылым: 2004.

2. абдула ж., мұқашева ә., сатаев л. жалпы физика курсының есептер

жинағы. –астана: 2006.

3. ақылбаев ж.с., гладков в.е., ильина л.ф. механика. -астана: 2005.

4. ақылбаев ж.с., құрманов м.к. физикалық терминдердің орысша-қазақша түсіндірме сөздігі. i, ii том. -алматы: 1994.

5. әкімбеков е.т. физика-1. оқу құралы. -астана: 2007.

6. әкімбеков е.т. физика-2. оқу құралы. -астана: 2008.

7. в.ветрова в.т. сборник задач по физике с индивидуальными заданиями.

-минск: 1991.

8. волькенштейн в.с. жалпы физика курсының есептер жинағы.

-алматы: 1974.

9. детлаф а.а, яворский б.м. курс физики. -м.: высш. шк., 2002.

10. қазақша-орысша, орысша-қазақша терминологиялық сөздік. т.1.:физика

және астрономия. -алматы: рауан, 1999.

11. қазақша-орысша, орысша-қазақша терминологиялық сөздік.

т.5.: энергетика. -алматы: рауан, 2000.

12. қазақша-орысша, орысша-қазақша терминологиялық сөздік.

т.6.: электроника, радиотехника және байланыс. -алматы: рауан, 2000.

13. құлбекұлы м. электр және магнетизмнің физикалық негіздері.

-алматы: қарасай, 2009.

14. орфографиялық сөздік. -алматы: тіл білімі институты, 2007.

15. савельев и.в. курс физики. –т.1-4. -м.: наука, 1989.

16. сена л.а. единицы физических величин и их размерности. -м.: 1998.

17. сивухин д.в. общий курс физики. –т.1-3. -м.: 1989.

18. сыздықов а. физика анықтамалығы. оқу құралы. -астана: 2008.

19. сыздықов а. физика анықтамалығы-2. оқу құралы. -астана: 2010.

20. трофимова т.и. курс физики. -м.: изд. центр «академия», 2007.

21. трофимова т.и. физика в таблицах и формулах. -м.: дрофа, 2002.

22. трофимова т.и. сборник задач по курсу физики для втузов.-м.: 2005.

23. фейнмановские лекции по физике. –т.1-6. -м.: мир, 1999.

24. физическая энциклопедия. 9-изд. -м.: наука, 1995.

Автономная некоммерческая организация высшего образования

«Институт бизнеса и дизайна»