Раздел 2. Задача. Исследовать функцию и построить её график.

Задача. Исследовать функцию 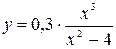и построить её график.

Решение:

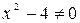1).Область определения функции т.к. при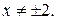

2).Исследуем функцию на четность

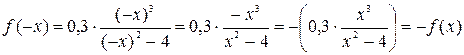
Функция нечетная, значит её график симметричен относительно начала координат.

3) Точки пересечения с осями. Если x=0, y=0.Следовательно, cуществует единственная точка пересечения с осями О(0;0).

4) Функция является непрерывной в своей области определения, а в точках -2 и 2, не принадлежащих D(y), имеет разрывы 2-го рода.

5).Найдем уравнения асимптот:

Вертикальные асимптоты. х= -2 и х= 2т.к.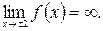

Наклонные асимптоты. 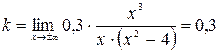и

Таким образом уравнение наклонной асимптоты имеет вид: у =0,3х.

6).Определим интервалы возрастания и убывания функции, а также критические точки. Для этого найдём первую производную нашей функции (достаточно найти только числитель, т.к. знаменатель всегда больше нуля). Числитель производной имеет вид: .

Отсюда видно, что на интервалах 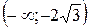и производная положительна, а значит исходная функция возрастает, а на интервалах 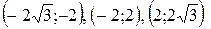производная отрицательна и поэтому на этих промежутках функция убывает.

Точки являются критическими. При переходе через точку 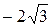прозводная меняет знак с минуса на плюс и поэтому в этой точке функция имеет

локальный максимум равный 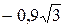. При переходе через точку 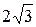произзводная меняет знак с плюса на минус и поэтому в этой точке функция имеет локальный минимум равный . При переходе через точку 0 производная знак не меняет, и поэтому в этой точке локального экстремума нет. В точках же -2 и 2 функция не определена.

7). Найдём интервалы, на которых график функции является выпуклым вверх или вниз.

Вторая производная функции имеет вид: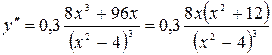

На интервалах 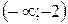и вторая производная меньше нуля, поэтому график функции является выпуклым вниз. На интервалах 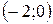и (2; ¥) вторая производная больше нуля, поэтому график функции является выпуклым вверх. В точке 0 вторая производная меняет знак, следовательно, в этой точке график функции имеет перегиб.

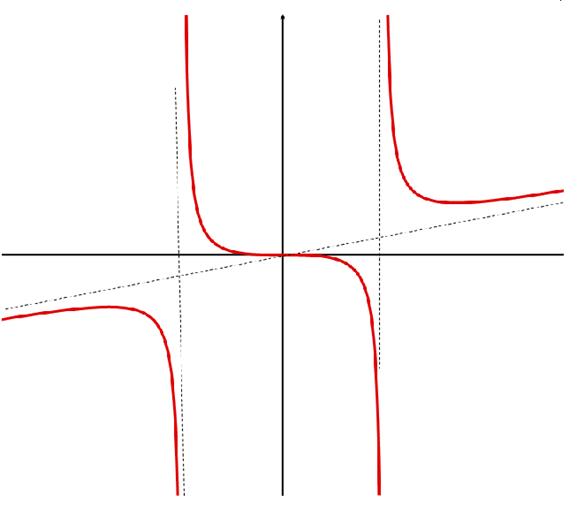
Используя проведённое исследование, можно построить график функции.