Раздел 3. Задача . Имеются три партии деталей по 20 деталей в каждой

Задача . Имеются три партии деталей по 20 деталей в каждой. Число стандартных деталей в них равно 20, 15 и 10 соответственно. Из произвольной партии наудачу извлечена деталь, оказавшаяся стандартной. Деталь возвращается в свою партию, и оттуда вторично берется деталь, которая также оказывается стандартной. Найти вероятность того, что детали извлекались из третьей партии.

Решение:

Эта задача на применение формулы Байеса. Мы не знаем из какой партии извлечена деталь. Поэтому выдвигаем гипотезы: Н₁ ={деталь извлечена из первой партии}, Н₂ ={деталь извлечена из второй партии}, Н₃ ={деталь извлечена из третьей партии}. Поскольку все партии равноправны, то Р(Н₁)=Р(Н₂)=Р(Н₃)=1/3. Условные вероятности вытаскивания (с возвращением) двух стандартных деталей из соответствующих партий равны

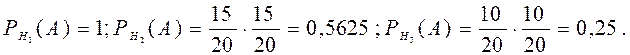
Подставляя эти значения в формулу Байеса, получаем

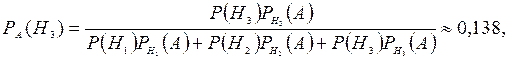
что в 2,5 раза меньше первоначальной вероятности третьей гипотезы. Это следствие того, что в третьей партии только половина деталей стандартна.