Расчет усиления процесса
Усиление процесса определяется как отношение изменения на выходе к изменению на входе.
В данном примере единицей измерения прибора для входного параметра, который является расходом топлива, является кл/ч, а единица измерения прибора для выходного параметра, который является температурой на выходе – градус C.
Для расчета усиления процесса и других параметров управления необходимо выполнить расчеты в стандартных единицах, а не в единицах соответствующих приборов. Таким образом, значения технологических параметров следует нормализовать относительно диапазонов измерения соответствующих приборов
PVNor= ( PVEU- RangeLo) /( RangeHigh- RangeLo)
Где:
PVNor — нормализованное значение PV в диапазоне от 0 до 1,
PVEU — значение PV в единицах прибора,
RangeHigh — верхний диапазон прибора, а
RangeLo — нижний диапазон прибора.
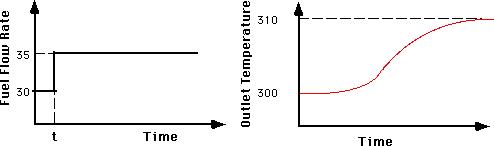
В случае с печным агрегатом температура на выходе меняется с 300 до 310 градусов C для изменения расхода топлива с 5 до 6 кл/ч.
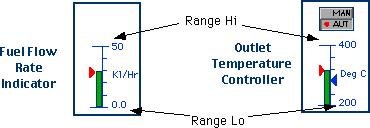
В данном примере контроллер расхода топлива имеет:
- Диапазон Hi: 50 кл/ч
- Диапазон Lo: 0 кл/ч
а контроллер температуры на выходе имеет:
- Диапазон Hi: 400 градусов C
- Диапазон Lo: 200 градусов C
Входящее значение меняется с 5 на 6 кл/ч. После нормализации этих значений относительно диапазона измерения расхода топлива прибора и расчета разницы, мы имеем:
(6-0)/(50 - 0) = 0,12
(5-0)/(50 - 0) = 0,1
Изменение на входе = 0,12 - 0,1 = 0,02
Выходное значение изменяется с 300 на 310 градусов C. После нормализации этих значений относительно диапазона измерения температуры на выходе прибора и расчета разности, мы имеем:
(310-200)/(400 - 200) = 0,55
(300-200)/(400 - 200) = 0,5
Изменение на выходе = 0,55 - 0,5= 0,05
Расчет усиления процесса выполняется путем получения отношения изменения на выходе к отношению на входе.
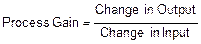
В нашем примере усиление процесса становится равным 0,5.
Усиление процесса = 0,05 / 0,01 = 0,5
Таким образом, протекание в динамических условиях процесса печного агрегата в нашем примере можно выразить в виде дифференциального уравнения первого порядка, а именно:
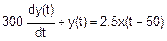
Математически данное уравнение также известно как "обыкновенное линейное дифференциальное уравнение первого порядка с постоянным коэффициентом".
В системе Лапласа это выражается следующим образом:
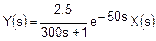
Дата добавления: 2014-12-02; просмотров: 1329;
