Типовая задача 2. Составить уравнение линии, если отношение расстояний от каждой ее точки до точки А(–1; 0) и до прямой х = –4 равно

Составить уравнение линии, если отношение расстояний от каждой ее точки до точки А(–1; 0) и до прямой х = –4 равно 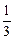. Построить график.

Решение. 1. Пусть М(х; у) — произвольная точка данной линии.

2. По формуле (1) находим расстояние 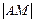и расстояние от точки М до ее проекции М₁на прямую х = –4:

= ,

= .

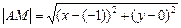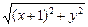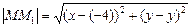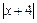По условию задачи, .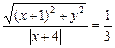

3. Преобразуем полученное уравнение:

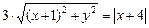
9 · (x² + 2x + 1 + y²) = x² + 8x + 16.

Отсюда 8х² + 10х + 9у² +(–7) = 0 =
= .

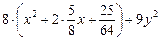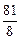
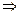
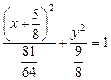С помощью формул параллельного переноса приведем уравнение к каноническому виду.

Пусть 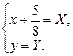(14)

Тогда уравнение линии запишем в виде 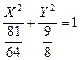. Это уравнение эллипса с полуосям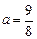и и 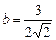. Так как 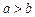, то фокусы его находятся на оси ОХ. Из формул (14) получаем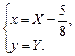

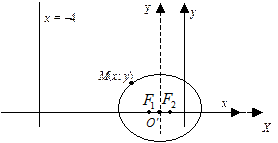
Точка О¢ 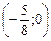есть начало новой системы координат ХОY относительно старой. Строим график данного эллипса в новой системе координат (рис. 8).

Ответ: .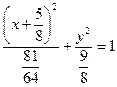
Рис. 8

2. Задания 3 и 4
по теме
«Элементы линейной алгебры и теории
n-мерных векторных пространств»