ОСНОВНЫЕ РАЗМЕРЫ ТРАНСФОРМАТОРА
Магнитная система трансформатора является основой его конструкции. Выбор основных размеров магнитной системы вместе с основными размерами обмоток определяет главные размеры активной части и всего трансформатора. Рассмотрим двухобмоточный трансформатор с плоской магнитной системой стержневого типа со стержнями, имеющими сечение в форме симметричной ступенчатой фигуры, вписанной в окружность, и с концентрическим расположением обмоток. Магнитная система такого трехфазного трансформатора с обмотками схематически изображена на рис. 3.5.
Диаметр d окружности, в которую вписано ступенчатое сечение стержня, является одним из его основных размеров. Вторым основным размером трансформатора является осевой размер l (высота) его обмоток. Обычно обе обмотки трансформатора имеют одинаковую высоту. Третьим основным размером трансформатора является средний диаметр витка двух обмоток, или диаметр осевого канала между обмотками d12, связывающий диаметр стержня с радиальными размерами обмоток a1 и а2 и осевого канала между ними a12.
Если эти три размера выбраны или известны, то остальные размеры, определяющие форму и объем магнитной системы и обмоток, например высота стержня lс, расстояние
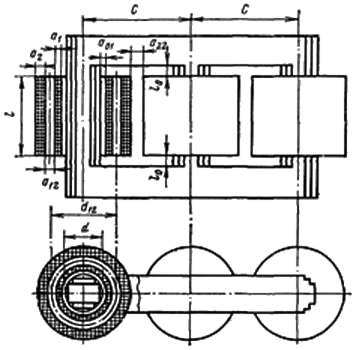
Рис. 3.5. Основные размеры трансформатора
между осями соседних стержней С т.д., могут быть найдены, если известны допустимые изоляционные расстояния от обмоток ВН до заземленных частей и до других обмоток (а12, а22, lо)*.
Два основных размера, относящихся к обмоткам d12 и 1с, могут быть связаны отношением средней длины окружности канала между обмотками πd12 к высоте обмотки l:
β = πd12/l (3.13)
Приближенно произведение πd12 можно приравнять к средней длине витка двух обмоток πd12≈lв или lв/ l =β.
Величина β определяет соотношение между диаметром и высотой обмотки. Значение β может варьироваться в широких пределах и практически изменяется в масляных и сухих трансформаторах существующих серий в пределах от 1 до 3,5. При этом меньшим значениям β соответствуют трансформаторы относительно узкие и высокие, большим— широкие и низкие. Это наглядно показано на рис. 3.6, на котором представлены два трансформатора одинаковой мощности, одного класса напряжения, рассчитанных при одинаковых исходных данных (Вс, kс), с одинаковыми параметрами короткого замыкания (Рк и ик) для значений β = 1,2 и 3,5.
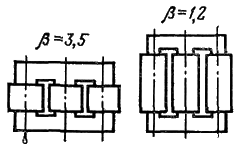
Рис. 3.6. Соотношение размеров двух трансформаторов с разными значениями β
Различным значениям β соответствуют и разные соотношения между массами активных материалов - стали магнитной системы и металла обмоток. Меньшим значениям β соответствует меньшая масса стали и большая масса металла обмоток. С увеличением β масса стали увеличивается, масса металла обмоток уменьшается. Таким образом, выбор β существенно влияет не только на соотношение размеров трансформатора, но и на соотношение масс активных и других материалов, а следовательно, и на стоимость трансформатора.
Вместе с этим изменение β сказывается и на технических параметрах трансформатора: потерях и токе холостого хода, механической прочности и нагревостойкости обмоток, габаритных размерах.
Для вывода формулы, связывающей диаметр стержня трансформатора с его мощностью, воспользуемся следующими соотношениями, известными из теории трансформаторов.
Мощность трансформатора на один стержень, кВ·А,
S' = UI·10-3 (3.14)
Реактивная составляющая напряжения короткого замыкания, %,
uр= 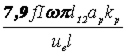 10-4
10-4
* Основными размерами можно считать также d, lс, С.
или
uр= 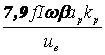 10-4 (3.15)
10-4 (3.15)
где β= πd12/l; аP= а12+(а1+а2)/3; kр - коэффициент приведения идеального поля рассеяния к реальному (коэффициент Роговского); линейные размеры выражены в метрах. Одновременно заметим, что напряжение витка трансформатора, В, может быть записано в виде
ив = 4,44 fBсПс, (3.16)
где Вс—максимальная индукция в стержне, Тл; Пс = kсπd2/4 - активное сечение стержня, м2; kс - коэффициент заполнения площади круга сталью согласно § 2.3.
Заменив в (3.14) напряжение обмотки U произведением ивω и подставив значение тока обмотки I, определенное из (3.15), и значение ив по (3.16), получим
S' = 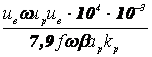 =
= 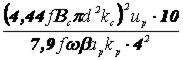 .
.
Проведя сокращения и решив это уравнение относительно d, имеем окончательно
d=0,507 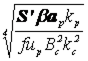 , (3.17)
, (3.17)
где
0,507 = 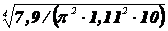 .
.
Формула (3.17) позволяет определить главный размер трансформатора - диаметр стержня его магнитной системы.
Величины, входящие в подкоренное выражение формулы (3.17), впервые предложенной Г. Н. Петровым, можно подразделить на три категории: 1) величины, заданные при расчете, - мощность обмоток на одном стержне трансформатора S', кВ·А, частота сети f, Гц, и реактивная составляющая напряжения короткого замыкания ир, %; 2) величины, выбираемые при расчете, — отношение длины окружности канала между обмотками (средней длины витка двух обмоток) к высоте обмотки β, максимальная индукция в стержне Вс, Тл, и коэффициент заполнения активной сталью площади круга, описанного около сечения стержня kс; 3) величины, определяемые в ходе последующего расчета, - приведенная ширина канала рассеяния ар, м, и коэффициент приведения идеализированного поля рассеяния к реальному kp (коэффициент Роговского).
Таким образом, определение диаметра стержня по (3.17) связано с выбором некоторых исходных данных (β, Вс, kc) и предварительным определением данных обмоток
трансформатора, получаемых обычно после завершения расчета обмоток ар и kp. Выбор исходных данных (β, Вс, kc) может быть сделан на основании исследования ряда вариантов (см. § 3.5—3.7) или путем использования заранее разработанных рекомендаций (см. § 3.7). Для определения ар и kp должны применяться приближенные методы.
Дата добавления: 2015-01-02; просмотров: 1614;
