Основные виды математических моделей

Математические модели могут быть:

1.) Линейными;

2.) Нелинейными

В свою очередь каждая из них может быть:

1.) Непрерывной (система дифференциальных или интегро-дифференциальных уравнений);

2.) Дискретной (система разностных уравнений);

3.) Дискретно-непрерывной (сочетание непрерывной и дискретной систем).

В свою очередь каждая из них может быть:

1.) Стационарной;

2.) Нестационарной.

Математическая модель нестационарна, если хотя бы один из параметров системы изменяется с течением времени.

В свою очередь каждая из них может быть:

1.) С сосредоточенными параметрами;

2.) С сосредоточенными и распределёнными параметрами.

1.) Физические параметры системы (например, масса, скорость, потенциал и др.) обычно сосредоточены в точке (так можно считать), коэффициенты дифференциальных уравнений зависят от этих параметров. В результате, математическая модель будет, например, системой дифференциальных уравнений в полных производных ( ).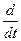

2.) Если система содержит одну из подсистем (например, канал связи, трубопровод), параметры которой распределены в пространстве, то математическая модель такой системы будет содержать, например, систему дифференциальных уравнений в частных производных ( ).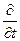

В свою очередь каждая из них может быть:

1.) Детерминированной;

2.) Стохастической или со случайными параметрами (если хотя бы один из параметров или воздействий является случайной функцией или величиной).