Решетчатые функции
Решетчатая функция (РФ) — функция, существующая в дискретны равноотстоящие друг от друга значения независимой переменной и равная нулю между этими значениями аргумента.
Пример такой функции:
смотри рисунок б) лекции №3.
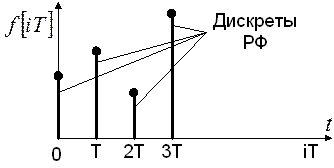
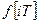 — РФ,
— РФ, 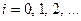
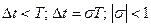
Функции f(t) соответствует функция 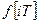 ,
, 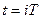 (
( 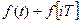 )
)
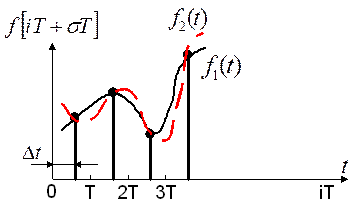
Одной и той же РФ соответствует множество огибающих непрерывных функций (смотри рисунок выше):
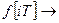
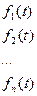 — огибающие функции.
— огибающие функции.
Если ввести безразмерное время 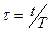 , то
, то 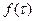 будет соответствовать РФ
будет соответствовать РФ 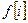 .
. 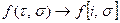
Решетчатую функцию характеризуют её разности и суммы
Разность может быть прямой ( 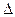 ) и обратной (
) и обратной ( 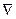 ).
).
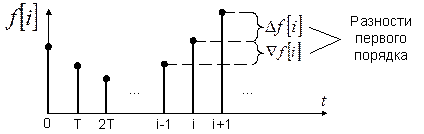
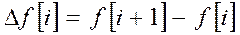
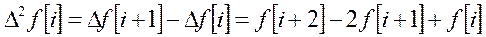
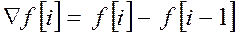
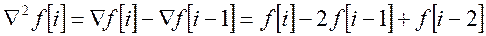
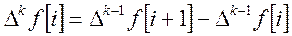 .
.
Аналогом интеграла непрерывной функции для РФ являются её суммы:
1) Полная 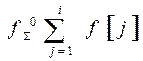 ;
;
2) Неполная 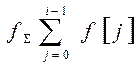 .
.
Дата добавления: 2015-01-02; просмотров: 721;
