МЕТОД Э. ЗИБЕЛЯ.

Широко известна методика, предложенная Э. Зибелем.

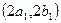Исходная квадратная ячейка делительной сетки при однородной деформации превращается в параллелограмм. Вписанная в исходный квадрат окружность превра­щается в эллипс (рис. 8.1). Фиксируются сопряженные диаметры , соединяющие точки касания эллипса со сторонами параллелограмма, и угол 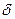между ними.

Рис. 8.1. Схема преобразования окружности в эллипс по Э. Зибелю

Главные оси эллипса определяются так:

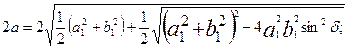
(8.1)

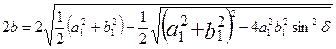
Угол между большой главной осью эллипса и большим сопряженным диаметром вычисляется по формуле:

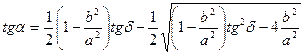(8.2)

Главные компоненты деформации находятся по уравнениям:

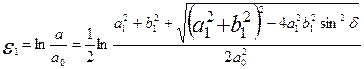; (8.3)

,

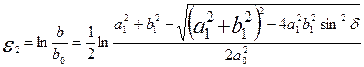а интенсивность деформации с учетом условия несжимаемости определяется так:

(8.4)

Для выполнения расчетов удобно пользоваться координатами точек Касания A, В, С и D, а полученные характеристики формоизменения считать локальными для точки 0 в центре ячейки (рис. 8.1).