Химический состав инструментальных сталей по ГОСТ 5950 - 73
| Марка стали | Химический состав, % | |||||||
| С | Мп | Si | Сг | W | V | Мо | Ni | |
| Р6М5 | 0,80 | - | - | 4,0 | 6,0 | 2,0 | 5,5 | - |
| ЗХЗМЗФ | 0,30 | 0,40 | 0,30 | 3,0 | - | 0,50 | 2,7 | - |
| 4Х5МФС | 0,37 | 0,30 | 1,0 | 5,0 | - | 0,4 | 1,3 | - |
Теплостойкость сталей (температура начала интенсивного разупрочнения) составляет следующие величины температур (закалка до HRC 40 - 60) Тр, К: Р6М5 - 933; ЗХЗМЗФ - 923; 4Х5МФС - 973.
В качестве независимых переменных (факторов) параметров модели были приняты следующие величины: 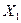 - температура испытания (t, °С); Х2 - удельная сила (q, МПа); Х3 - скорость деформирования (производительность) (и, ход/мин). Параметром оптимизации, т.е. исследуемой величиной, является у
- температура испытания (t, °С); Х2 - удельная сила (q, МПа); Х3 - скорость деформирования (производительность) (и, ход/мин). Параметром оптимизации, т.е. исследуемой величиной, является у 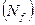 - число циклов до появления трещины на рабочей поверхности шарового сегмента образца-пуансона. Вычисление общей стойкости
- число циклов до появления трещины на рабочей поверхности шарового сегмента образца-пуансона. Вычисление общей стойкости 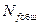 рабочей конструкции пуансона производилось с учетом следующего выражения, при условии, что изменение параметров испытания не выходит за рамки предлагаемого варианта технологического процесса, т.е.
рабочей конструкции пуансона производилось с учетом следующего выражения, при условии, что изменение параметров испытания не выходит за рамки предлагаемого варианта технологического процесса, т.е.
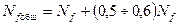 . (5.1)
. (5.1)
Интервалы варьирования факторов и их значения в натуральном масштабе на основном, верхнем и нижних уровнях приведены в табл. 5.2.
Таблица 5. 2
Уровни факторов
| Факторы | 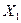 ( t°C) ( t°C)
| 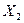 ( q, МПа) ( q, МПа)
| 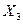 (п, ход/ мин') (п, ход/ мин')
|
Основной уровень 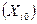
| |||
Интервал варьирования 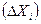
| |||
Верхний уровень 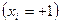
| |||
Нижний уровень 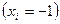
|
Кодированные значения факторов 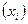 связаны с натуральными
связаны с натуральными 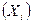 следующими соотношениями:
следующими соотношениями:
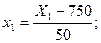
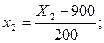
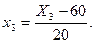 (5.2)
(5.2)
Для получения возможно полной информации об изучаемых зависимостях использовался полный факторный эксперимент первого порядка 23, в котором реализуются все возможные сочетания фактором и как наиболее простой для практических расчетов, обеспечивающий достаточно хорошее приближение.
Математическая модель исследуемого процесса выражается о помощью следующего уравнения:
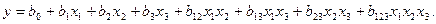 (5.3)
(5.3)
Для определения коэффициентов регрессии 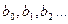 математической модели стойкости образца-пуансона проводится полный трехфакторный эксперимент на верхнем и нижнем уровнях независимых переменных. Для получения сочетания уровней факторов проводится 8 опытов, что позволяет с достаточной точностью определить область оптимальных значений стойкости образца-пуансона в зависимости от основных технологических факторов. В случае изменения значений коэффициентов регрессии (предлагается иной вариант технологии, предопределяющей иные выходные параметры выдавливания), может измениться и сама функция (модель). Таким образом, для поиска оптимального значения стойкости модели (образца - пуансона) составляется матрица планирования эксперимента. План эксперимента в кодовом и натуральном масштабах с полученными усредненными результатами величин стойкости приведен в табл. 5.3.
математической модели стойкости образца-пуансона проводится полный трехфакторный эксперимент на верхнем и нижнем уровнях независимых переменных. Для получения сочетания уровней факторов проводится 8 опытов, что позволяет с достаточной точностью определить область оптимальных значений стойкости образца-пуансона в зависимости от основных технологических факторов. В случае изменения значений коэффициентов регрессии (предлагается иной вариант технологии, предопределяющей иные выходные параметры выдавливания), может измениться и сама функция (модель). Таким образом, для поиска оптимального значения стойкости модели (образца - пуансона) составляется матрица планирования эксперимента. План эксперимента в кодовом и натуральном масштабах с полученными усредненными результатами величин стойкости приведен в табл. 5.3.
Таблица 5.3
| План 23 и результаты опытов | |||||||||||||
| № опыта | Кодовый масштаб | Натуральный масштаб | Марки сталей | ||||||||||
| опы- та | Р6М5 | ЗХЗМЗФ | 4Х5МФС | ||||||||||
| 
| 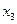
| 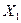 (t°С) (t°С)
| 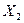 (q,МПа)
(q,МПа)
| 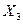 (п, мин 1)
(п, мин 1)
| 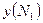
| 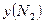
| 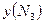
| |||||
| + | + | + | |||||||||||
| - | + | + | |||||||||||
| + | - | + | |||||||||||
| - | - | + | |||||||||||
| + | + | - | |||||||||||
| - | + | - | |||||||||||
| + | - | - | |||||||||||
| - | - | - | |||||||||||
Расчет уравнения регрессии, представляющего собой зависимость числа циклов стойкости 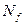 образца - пуансона от изучаемых факторов, проводится применительно для стали марки Р6М5.
образца - пуансона от изучаемых факторов, проводится применительно для стали марки Р6М5.
Коэффициенты регрессии biопределяются по формуле:
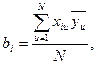
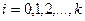 (5.4)
(5.4)
где i - номер фактора; и - порядковый номер опыта; N - число опытов; 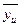 - среднее арифметическое значение результатов параллельных опытов.
- среднее арифметическое значение результатов параллельных опытов.
Дисперсия параметра оптимизации находится по выражению:
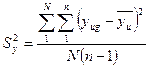 , (5.5)
, (5.5)
где yug- результат g -го повторения и - го опыта;
n - число параллельных опытов в строке матрицы планирования.
Для каждого опыта рассчитывается построчная дисперсия 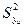 .
.
Проверяется однородность ряда построчных дисперсий по величине критерия Кохрена.
В данном случае 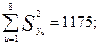
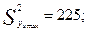 поэтому
поэтому
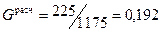 . При
. При 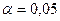 устанавливается число степеней свободы
устанавливается число степеней свободы
ƒ = n -1 = 2 с числом опытов N = 8, и выбирается табличное значение
G- критерия: 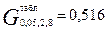 .
.
Поскольку выполняется условие Gpaсч < Gmaбл, т. е. 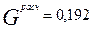 <0,516, ряд дисперсии считается однородным.
<0,516, ряд дисперсии считается однородным.
Далее по формуле
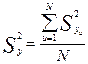 (5.6)
(5.6)
рассчитывается дисперсия опыта 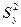 =1175/8 = 146,9 с учетом, что
=1175/8 = 146,9 с учетом, что
ƒ = N(n -1) - число степеней свободы, т.е. ƒ = 8(3 -1) = 16.
Коэффициенты регрессии, подсчитанные по формуле (5.4), оказались следующими:
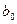 = 2706,25;
= 2706,25; 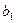 = - 93,75;
= - 93,75; 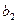 = - 206,25;
= - 206,25; 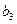 = - 218,75;
= - 218,75;
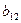 = - 6,25;
= - 6,25; 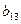 = 6,25;
= 6,25; 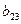 = 28,75;
= 28,75; 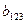 = - 6,25.
= - 6,25.
Полученные коэффициенты регрессии проверяются на статическую значимость по критерию Стьюдента. Дисперсия оценок коэффициентов рассчитывается по формуле:
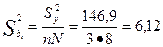 .
.
Среднеквадратичная ошибка составляет 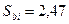 .
.
Выбирается уровень значимости 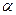 = 0,05 и, взяв при числе степеней свободы
= 0,05 и, взяв при числе степеней свободы
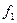 =16, табличное значение t - критерия, равным
=16, табличное значение t - критерия, равным 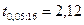 ,
,
по формуле : 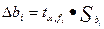 - подсчитывается доверительный интервал коэффициентов регрессии, который получается равным:
- подсчитывается доверительный интервал коэффициентов регрессии, который получается равным:
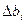 =2,12
=2,12 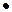 2,47=5,24.
2,47=5,24.
После подстановки коэффициентов в выражение (5.3) получается следующее уравнение регрессии:
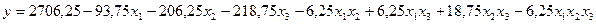 (5.7)
(5.7)
Проверка адекватности полученной модели проводится с помощью
F-критерия (критерия Фишера). Его расчетное значение следующее:
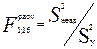 , где
, где 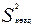 - дисперсия неадекватности, которая вычисляется по формуле:
- дисперсия неадекватности, которая вычисляется по формуле:
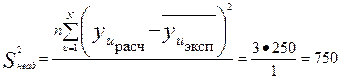 (5.8)
(5.8)
Тогда имеем: 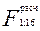 = 750/146,9 = 5,11.
= 750/146,9 = 5,11.
При уровне значимости 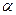 = 0,05 табличное значение F-критерия
= 0,05 табличное значение F-критерия
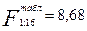 . Поскольку
. Поскольку 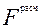 <
< 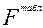 гипотеза об адвекватности модели (18) при 5 % - ом уровне значимости не отвергается.
гипотеза об адвекватности модели (18) при 5 % - ом уровне значимости не отвергается.
 Из анализа уравнения (5.7) видно, что стойкость инструмента (у) значительно зависит от величины удельной силы
Из анализа уравнения (5.7) видно, что стойкость инструмента (у) значительно зависит от величины удельной силы 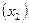 , скорости деформирования
, скорости деформирования 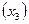 и в меньшей мере от температуры процесса
и в меньшей мере от температуры процесса 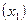 . Причем, влияние удельной силы
. Причем, влияние удельной силы 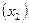 сопоставимо со скоростью деформирования
сопоставимо со скоростью деформирования 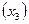 . Благоприятно влияют на стойкость двойное взаимодействие между температурой, удельной силой и скоростью деформирования (
. Благоприятно влияют на стойкость двойное взаимодействие между температурой, удельной силой и скоростью деформирования ( 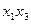 и
и 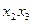 ), остальные эффекты слабы.
), остальные эффекты слабы.
Как показывают расчеты, при уменьшении числа ходов пресса до 12 в минуту стойкость пуансона увеличивается в 3-4 раза и может составить порядка 10000 циклов.
Заменив условные обозначения переменных факторов их истинными величинами, уравнение после несложных преобразований записывается в следующем виде для остальных марок сталей:
- для стали Р6М5:
Y = 7075 - 3,38t - 2,25q - 40,9n +0,00125tq + 0,034tn + 0,028qn - 0,00003tqn ; (5.9)
- для стали ЗХЗМЗФ:
y= 7450 - 2,38t - 1,50q – 37,2 n +0,00125tq +0,044tn - 0,004qn - 0,00006tqn; (5.10)
- для стали 4Х5МФС:
y= 7575 - 1,88t - 1,25q – 18,1 n +0,00125tq +0,022tn - 0,019qn - 0,00003tqn; (5.11)
При изготовлении элементов приводных и тяговых цепей степень деформации не превышает величины ε = 0,55. Материал заготовки - сталь 30ХНЗА. Удельная сила полугорячего обратного выдавливания на прессе составляет не более 800 - 1000 МПа. Представляет практический интерес оценка стойкости пуансона для обратного выдавливания при получении поковки ролика приводной цепи, например, с шагом 25,4 мм в условиях массового производства. Материал пуансона - инструментальная сталь марки Р6М5. Расчет осуществляется для случая выдавливания пуансоном с диаметром dn =11,5 мм, диаметр заготовки D3 =15,8 мм при температуре t = 760 °С, удельная сила составляет q = 800 МПа и производительность п = 50 ходов в минуту.
После подстановки исходных данных в уравнение (5.9) получаем:
у=7075-3,38760-2,25-800-40,9-50 + 0,00125-760-800 + 0,034-760-50 + 0,028-800-50-0,00003-760-800-50= 2921шт.

Рис. 5.1. Сопротивление
Дата добавления: 2014-12-30; просмотров: 1606;
