ФИЗИЧЕСКОЕ МОДЕЛИРОВАНИЕ. КРИТЕРИИ ПОДОБИЯ.
Физическое моделирование основано на создании физического аналога изделия, отличающегося от натурального образца, в основном, масштабом. Необходимым условием является сохранение подобия модельного и натурного образца и условий их функционирования.
Существуют различные способы определения механического или физического подобия. Для практики удобно определения подобия в такой форме.
Два явления подобны, если по заданным характеристикам одного можно получить характеристики другого простым пересчетом, который аналогичен переходу от одной системы единиц измерения к другой системе.Для осуществления пересчета необходимо знать так называемые «переходные масштабы".
Численные характеристики для двух различных, но подобных явлений можно рассматривать как численные характеристики одного и того же явления, выраженныев двух различных системах единиц измерения. Для всякой совокупности подобных явлений все безразмерные характеристики (безразмерные комбинации из размерных величин) имеют одинаковое численное значение. Нетрудно видеть, что обратноезаключение также справедливо, т.е. если все безразмерные характеристикидля двух движений одинаковы, то движения подобны.
Для сохранения подобия при моделировании необходимо соблюдать некоторые условия.Однако, не практике сплошь и рядом эти условия, обеспечивающие подобие явления в целом, не выполняются, и тогда встает вопрос о величине погрешностей (масштабном эффекте), которые возникают при переносе на натуру результатов, полученных на модели.
 После установления системы параметров, определяющих выделенный класс явлений, нетрудно установить условия подобия двух явлений.
После установления системы параметров, определяющих выделенный класс явлений, нетрудно установить условия подобия двух явлений.
 Пусть явление определяется nпараметрами, часть которых может быть безразмерными, а некоторые являются размерными физическими постоянными. Допустим далее, что размерности переменных параметров и физических постоянных выражены через k величин с независимыми размерностями (k≤n). В общем случае, очевидно, что из nвеличин можно составить не более n - kнезависимых безразмерных комбинаций. Все безразмерные характеристики явления можно рассматривать как функции от этих n- k независимых безразмерных комбинаций, составленных из определяющих параметров. Следовательно, среди всex безразмерных величин, составленных из характеристик явления, всегда можно указать некоторую базу, т.е. систему безразмерных величин, которые определяют собой все остальные величины.
Пусть явление определяется nпараметрами, часть которых может быть безразмерными, а некоторые являются размерными физическими постоянными. Допустим далее, что размерности переменных параметров и физических постоянных выражены через k величин с независимыми размерностями (k≤n). В общем случае, очевидно, что из nвеличин можно составить не более n - kнезависимых безразмерных комбинаций. Все безразмерные характеристики явления можно рассматривать как функции от этих n- k независимых безразмерных комбинаций, составленных из определяющих параметров. Следовательно, среди всex безразмерных величин, составленных из характеристик явления, всегда можно указать некоторую базу, т.е. систему безразмерных величин, которые определяют собой все остальные величины.
Всоответствии с этим выделение подкласса подобных явлений осуществляется с помощью следующего условия.
Необходимым и достаточным условием подобия двух явлений будет постоянство численных значений безразмерных комбинаций, образующих базу. Условия о постоянстве базы отвлеченных параметров, составленных из заданных, определяющих явление величин, называются критериями подобия.
Если все условия подобия выполнены, то для фактического расчета всех характеристик в натуре по данным о размерных характеристиках на модели необходимо знать переходные масштабы для всех соответствующих величин.
Например, в задаче об установившемся поступательном плоско параллельном движениитела в несжимаемой вязкой жидкости все безразмерные величины определятся двумя параметрами: углом атаки αи числом Рейнольдса Rе. Условия физического подобия - критерии подобия - представляются соотношениями
α= c o n s t и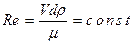
При моделировании этого явления результаты опытов с моделью можно переносить на натурутолько для одинаковых α и Rе. Первое условие всегда легко осуществитьна практике. Труднее удовлетворить второму условию (Rе = c o n s t) ,  особенно в тех случаях, когда обтекаемое тело имеет большие размеры, как, например, крыло самолета. Если модель меньше натуры, то необходимо либо увеличивать скорость обтекающего потока, что практически обычно неосуществимо, либо существенно изменять плотность и вязкость жидкости.
особенно в тех случаях, когда обтекаемое тело имеет большие размеры, как, например, крыло самолета. Если модель меньше натуры, то необходимо либо увеличивать скорость обтекающего потока, что практически обычно неосуществимо, либо существенно изменять плотность и вязкость жидкости.
На практике эти обстоятельства вносят большие затруднения при изучении аэродинамического сопротивления. Необходимость постоянства Числа Рейнольд-са привела к постройке гигантских аэродинамических труб, в которых можно производить продувки самолетов в натуру, а также труб закрытого типа, в которых циркулирует с большой скоростью сжатый, т.е. более плотный воздух.
Рассмотрим в качестве другого примера задачу о моделировании равновесия упругих конструкций.
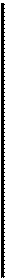 Пусть мы имеем какое - нибудь сооружение из однородного материала, на - пример, мостовую ферму. Упругие свойства изотропного материала определяются двумя постоянными: модулем Юнга Е кГ/м² и безразмерным коэффициентом Пуассона µ. Рассмотрим геометрически подобные конструкции и составим таблицу определяющих параметров.
Пусть мы имеем какое - нибудь сооружение из однородного материала, на - пример, мостовую ферму. Упругие свойства изотропного материала определяются двумя постоянными: модулем Юнга Е кГ/м² и безразмерным коэффициентом Пуассона µ. Рассмотрим геометрически подобные конструкции и составим таблицу определяющих параметров.
Для определения всех размеров модели достаточно задать некоторый характерный ее размер В. Если в рассматриваемом состоянии равновесия вес конструкции существенен, то удельный вес γ= ρg кГ/ м³ должен фигурировать в качестве определяющего параметра. Кроме силы веса частей сооружения, на него действуют еще внешние нагрузки, распределенные некоторым определенным способом по элементам конструкции. Пусть величина этих нагрузок определяется силой Ркг. Итак, системой определяющих параметров будет µ, Е, В, γ = ρg, Р.
В этомслучае мы имеем n =5, k =2, следовательно, базой для механических подобныхсостояний упругого равновесия будут три безразмерных параметра: µ, 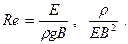
Критерии подобия заключаются в равенстве этих параметров на модели и в натуре.При выполнении этих условий все деформации будут подобными. Если модель в nраз меньше натуры, то на модели деформации будут в nраз меньше, чемв натуре.
Если модель и сооружение в натуре выполнены из одного и того же материала, то значения ρ, µиЕ одинаковы на модели и в натуре, поэтому для механического подобия необходимо удовлетворить условию
gb = const
В обычных условиях g = соnst ; следовательно, для соблюдения механического подобия должно быть В = соnst , т.е. модель должна совпадать с натурой. Иначе говоря, при постоянном gмоделирование невозможно.
Изменение g можно достигнуть искусственным путем, если заставить модель вращаться с постоянной угловой скоростью, поместив ее на центробежную машину. При вращении на модель будут действовать массовые силы, аналогичные силе тяжести, но только с другим ускорением. Выбором угловой скорости вращения можно получать любые большие значения для ускорения.
Дата добавления: 2014-12-30; просмотров: 2543;
