Всякое физическое тело (система), поставленное в определённые внешние условия, рано или поздно приходит в состояние термодинамического (статистического) равновесия.

Если система поставлена в определённые внешние условия (то есть, заданы её внешние параметры), но она находится в неравновесном состоянии (то есть её внутренние параметры не имеют равновесных значений), то система изменяется во времени, приближаясь к своему равновесному состоянию.

Нередко бывает, что скорость изменения внутреннего параметра 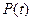пропорциональна его отклонению от равновесного значения 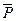; в этом случае

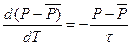, (2)

где 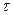- постоянный множитель, называемый временем релаксации.

Интегрируя это выражение, получим

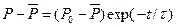(3)

Здесь 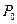- неравновесное значение параметра 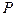в начальный момент времени .

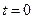Из соотношения (3) видно, что 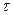- время, в течение которого отклонение параметра от его равновесного значения уменьшается в 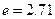раза. Время релаксации 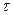зависит не только от природы внутреннего параметра 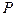, но и от характера нарушения его равновесного значения. Например, если 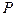давление в данной точке внутри газа, то 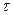, связанное с нарушением равновесного распределения молекул по скоростям, - другое.

В силу этого зависимость 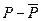от времени может быть более сложной, чем (3); так, например, 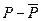может равняться сумме экспоненциальных членов с разными временами релаксации 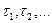. Возможен и такой случай, когда зависимость 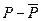от времени имеет характер затухающих колебаний.

Если в системе реализуется термодинамическое равновесие только в отношении части переменных, описывающих систему, то говорят о неполном термодинамическом равновесии.

Величина времени релаксации может меняться в очень широких пределах.

Например, при нарушении равновесного распределения молекул газа по скорости время релаксации для давления имеет порядок среднего времени между двумя последовательными столкновениями молекул; для газа, находящегося при нормальных условиях ( 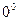Цельсия и атмосферное давление), это время 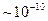сек. С другой стороны, обычное стекло представляет собой аморфное тело, не находящееся в состоянии термодинамического равновесия. Известно, что в течение длительных промежутков времени, измеряемых годами и даже десятками лет, аморфное стекло переходит в равновесное кристаллическое состояние. В этом случае 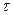порядка десятков лет, то есть примерно в 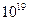раз больше, чем в предыдущем случае. В случае стекла имеет место своеобразная ситуация, когда в системе осуществляется статистическое равновесие молекул по скоростям, но не имеет места равновесие по положениям молекул в пространстве.

Уравнение состояния идеального газа имеет вид.

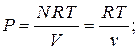
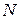- полное число молей в газе; 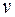- объем одного моля; 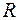- универсальная газовая постоянная. Соответственно, зависимость давления от объема при этих температурах близка к гиперболе.

Реальный газ. Вириальное уравнение состояния. Уравнение Ван – дер - Ваальса.

Для реальных газов термическое уравнение состояния 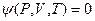в общем виде записывается так

,

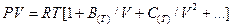где 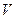– мольный объём газа; 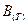, , 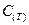… - второй, третий и т.д. вириальные коэффициенты. Само уравнение называется вириальным уравнением состояния(Каммерлинг – Онесс).

Принципиально можно теоретически рассчитать вириальные коэффициенты с той или иной степенью точности. Но это довольно сложная проблема, которая в конце курса ещё будет затронута.

Вычислив 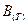, , 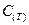…, получим уравнение состояния для конкретного газа.

Лучше было бы получить уравнение состояния, которое описывало поведение всех реальных газов, несмотря на потери в точности.

Впервые эту задачу решил голландский физик Ван-дер-Ваальс в своей диссертации "Непрерывность газообразного и жидкого состояния" (1873 г.). Такое уравнение состояния должно учитывать взаимодействие молекул, т.е. силы притяжения и отталкивания между молекулами.

Простые и не очень строгие рассуждения привели к уравнению вида

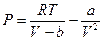или (*)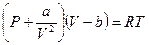

Уравнение называется уравнением состояния Ван-дер-Ваальса.Вывод сделан на основе качественных рассуждений о молекулярном объёме "b" и межмолекулярных силах притяжения, величина которых пропорциональна квадрату плотности газа. Но в этом и сила этого подхода. Не надо точно знать, что происходит между молекулами. К величинам "а" и "b" можно относиться как к подгоночным параметрам. А сходство реальных изотерм в Р, V – диаграмме с изотермами Ван-дер-Ваальса говорит о силе этого уравнения.

Постижение движущей силы

Проблема моделирования состояния вещества в метастабильной области сводится к определению способа продолжения различных термодинамических линий (изохор, изотерм, изобар) за пограничную кривую. Из того, что известно о метастабильных состояниях, можно ожидать плавного, без каких либо особенностей, изменения термодинамических параметров при постепенном углублении в «чужую» область (например, перегреве жидкости).

Рассматривая в качестве движущей силы системы в точке A разность потенциала Гиббса метастабильного и равновесного состояний системы, необходимо придумать способ продолжения вышеуказанных термодинамических линий в метастабильную область за кривую MN. При этом предполагается, что равновесные термодинамические параметры системы известны.

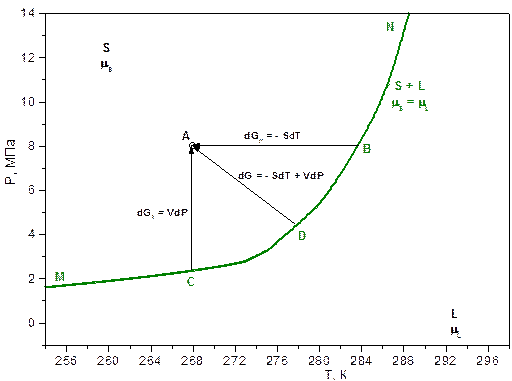
Однокомпонентная жидкость.

Вычислим энергию Гиббса однокомпонентного вещества в точке А (метастабильной жидкости и твёрдого тела).

Для однокомпонентной жидкости термодинамический потенциал Гиббса является характеристической функцией с параметрами 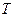и .

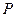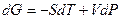(1)

На кривой MN в равновесии находятся твёрдая и жидкая фазы. В точках B,C и D химические потенциалы (парциальные мольные энергии Гиббса) компонентов твёрдой и жидкой фаз равны: 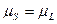. Исследуем три случая.

1. Изобарический: .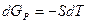

Для метастабильной жидкости:

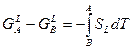(2)

Для твёрдого тела:

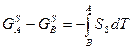(3)

Объединяя (2) и (3) получаем:

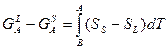(4)

Фазовые превращения, вообще говоря, сопровождаются скачкообразными изменениями энтропии. Это означает, что при таких превращениях поглощается или выделяется тепло. Например, при переходе единицы массы вещества из газообразного состояния 1 в жидкое 2 выделяется тепло

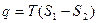(5)

При обратном переходе из жидкого состояния 2 в газообразное 1 такое же тепло поглощается. Предполагается, что переход совершается квазистатически при постоянной температуре, а, следовательно, и при постоянном давлении. Тепло 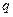называется удельной теплотой испарения. В общем случае оно называется удельной теплотой фазового превращения. Например, говорят о теплоте плавления, теплоте возгонки и пр.

Первое приближение.

Подставляя (5) в (4) получаем:

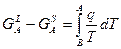(6)

Продолжение соотношений (5) и (6) в метастабильную область.

2. Изотермический: .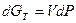

Для метастабильной жидкости:

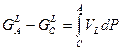(7)

Для твёрдого тела:

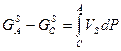(8)

Объединяя (2) и (3) получаем:

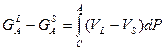(9)

Первое приближение.

3. Общий: .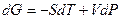

Для метастабильной жидкости:

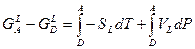(10)

Для твёрдого тела:

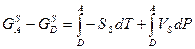(11)

Объединяя (2) и (3) получаем:

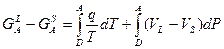(12)

Продолжение соотношения (12) в метастабильную область.

Первое приближение.

1. M.Folmer. Kinetik der Phasenbildung. Dresden – Leipzig. 1939.

2. Н. Дас Гупта, С. Гош. Камера Вильсона и её применения в физике. ИЛ, М. 1947.

3. В.И. Данилов. Строение и кристаллизация жидкости. Изд. АН УССР. Киев. 1956.

4. Д. Хирс, Г. Паунд. Испарение и конденсация. Изд. «Металлургия», М. 1966.

5. А.Г. Амелин. Теоретические основыобразования тумана при конденсации пара. Изд. «Химия». М. 1966.

6. Б. Чалмерс. Теория затвердевания. Изд. «Металлургия», М. 1968.

в обзорных статьях:

7. Д.Н. Холломон. Д. Тарнбалл. Успехи физики металлов. т.1. Металлургиздат. М., 1956. стр. 304.

17. J. Feder, K.C. Russell, J.Lothe, G.M.Pond. Adv. Phys., 15, №57, 111, (1966).

18. Debenedetti, P.G., Metastable Liquids, Concepts and Principles, Princeton University Press, NJ (1996).

19. Debenedetti, P.G., J. Phys.: Condens. Matter, 15, R1669 (2003).

Всякое физическое тело (система), поставленное в определённые внешние условия, рано или поздно приходит в состояние термодинамического (статистического) равновесия.

Для равновесной системы справедливо правило фаз Гиббса. которое записывается в следующем виде:

F = K – Ф + 2,

где К – число компонентов в системе, Ф – число фаз.

Кстати, для системы в пористых средах:

F = K – Ф + 3,

то есть система имеет на одну степень свободы больше по сравнению со свободным объёмом. Возможно формирование дополнительной фазы в пористой среде.

F = 0 – нонвариантная система, F = 1 – моновариантная система, F = 0 – бивариантная система, и т.д.

Фазовое поведение смесей углеводород + вода значительно отличается от фазового поведения смесей нормальных углеводородов (об их фазовом поведении мы будем говорить в курсе теории фазовых переходов …). Различия возникают от двух эффектов, каждый из которых проистекает от водородных связей.

Первый, фаза гидрата покрывает значительную часть всех фазовых диаграмм углеводород + вода для углеводородов с молекулярным размером меньшим .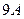

Второй, молекулы воды и углеводородов настолько различны, что в конденсированном состоянии образуются две жидкие различные фазы, каждый компонент которой очень мало растворим в другой фазе.