Сложение двоичных кодов
Сложение прямых кодов двоичных чисел редко применяется в вычислительной технике, поскольку при сложении чисел с разными знаками для формирования знака суммы требуется выполнение дополнительной нетривиальной процедуры. Гораздо проще складывать числа, представленные инверсными кодами, поскольку в этом случае знаковые разряды операндов, как и все остальные разряды, можно складывать по правилам двоичной арифметики, что приводит к автоматическому формированию знака суммы.
При сложении чисел с плавающей запятой на первом этапе необходимо сравнить порядки операндов. Если порядки слагаемых разные, это означает, что разряды мантисс операндов имеют разные веса и прямое сложение таких операндов невозможно. Поэтому перед выполнением сложения мантисс следует осуществить выравнивание порядков операндов.
Для выравнивания порядков операндов вычисляется разность порядков первого второго слагаемых DP = (P1 – P2) на сумматоре порядков. Очевидно, что операция вычитания (P1 – P2) должна заменяться операцией сложения P1 + (–P2), при этом оба порядка должны быть представлены в инверсном коде с учетом инвертированного знакового разряда вычитаемого.
Если DP = 0, то порядки слагаемых равны и можно переходить к сложению мантисс. Если разность порядков положительная (DP > 0), то первое слагаемое больше второго. В этом случае следует сдвинуть мантиссу второго слагаемого на DP разрядов вправо, а порядок второго слагаемого увеличить на DP. Когда разность порядков отрицательная (DP < 0), первое слагаемое меньше второго, поэтому следует сдвинуть мантиссу первого слагаемого на |DP| разрядов вправо, а порядок первого слагаемого увеличить на |DP|.
Возможен вариант, когда |DP| больше, чем число цифровых разрядов мантиссы, что приводит к обнулению одного из операндов. Тогда вместо уравнивания порядков следует сразу сформировать код суммы, равный коду большего слагаемого.
Поскольку порядки слагаемых могут быть с разными знаками, то при нахождении их разности может возникнуть переполнение сумматора порядков. Для фиксации переполнения часто используют модифицированный код с удвоенным знаковым разрядом, поскольку в результате переполнения при сложении единица переноса выходит из старшего разряда мантиссы суммы и знак суммы будет изменен.
При использовании модифицированного кода двоичная комбинация «01» в знаковых разрядах суммы указывает на положительное переполнение в сумматоре порядков. В этом случае в качестве результата сложения следует выдать код первого слагаемого. Если в знаковых разрядах суммы окажется двоичная комбинация «10», это указывает на отрицательное переполнение. Тогда в качестве результата сложения следует выдать код второго слагаемого.
После выравнивания порядков производится сложение мантисс операндов по правилам двоичной арифметики и округление результата (подробнее об операции округления можно прочитать в разделе 2.3 настоящего пособия). При этом возможна денормализация результата как влево (переполнение в сумматоре мантисс), так и вправо. Денормализованное на k разрядов вправо число оказывается по модулю меньше 0,5. В табл. 2.1 представлены изображения денормализованных чисел в прямом и инверсном кодах.
Таблица 2.1
| Положительное | Отрицательное | |||||
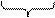
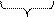
| 0,00…01… | 1,00…01… | ||||
|
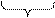
| 0,00…01… | 1,11…10… |
При фиксации в сумматоре мантисс переполнения необходимо ликвидировать его путем сдвига содержимого сумматора вправо на один разряд, при этом в освобождающийся старший знаковый разряд заносится цифра, оказывающаяся в результате сдвига в младшем знаковом разряде, а порядок суммы увеличивается на 1. Если при сложении мантисс возникла денормализация результата на k разрядов вправо, то для ее устранения необходимо сдвинуть результат на k разрядов влево, а порядок результата следует уменьшить на k. При этом необходимо учитывать возможность появления запрещенной в дополнительном коде комбинации «1,00…0» и равенство суммы нулю.
В том случае, когда денормализованное вправо отрицательное число представлено в обратном коде, освобождающиеся при сдвиге влево разряды мантиссы следует заполнять единицами, в других случаях – нулями.
Поскольку при устранении денормализации должно изменяться значение порядка, то может иметь место переполнение в сумматоре порядков. При положительном переполнении результат приравнивается к бесконечности, знак которой определяется знаком мантиссы. При отрицательном переполнении в сумматоре порядков результат считается бесконечно малой ненулевой величиной (если мантисса отлична от нуля).
Рассмотрим несколько примеров сложения чисел в дополнительном коде. Обозначим мантиссы операндов через [mX], порядки – через [PХ].
Пример 1.
A(10) = 20,25; B(10) = -0,75; C = A + B;
A(2) = 10100,01; B(2) = -00000,11;
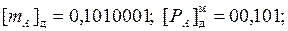
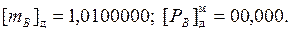
1. Для выравнивания порядков вычислим 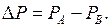

|
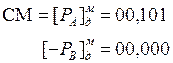
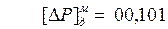
Поскольку в сумматоре порядков образовалось положительное число, операнд A больше операнда B. Для выравнивания порядков сдвинем мантиссу второго операнда на DP разрядов вправо:

2. Выполним сложение мантисс, при этом в сумматоре введем дополнительный младший разряд для округления.


|
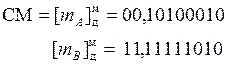
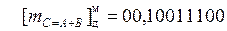
После округления до семи разрядов после запятой получим
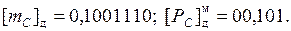
Таким образом, С(2) = 10011,10; С(10) = 19,5.
Пример 2.
А(2) = 0,01101011; В(2) = -0,01000111; C = A + B;
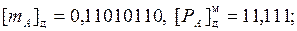
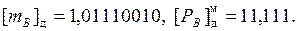
1. Для выравнивания порядков вычислим 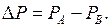
|

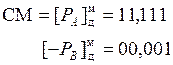
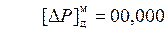
Разность порядков равна 0, следовательно, уравнивание не требуется.
2. Выполним сложение мантисс.

|
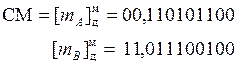

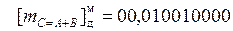
После округления до восьми разрядов после запятой получим
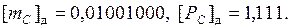
Мантисса суммы оказалась денормализованной на один разряд вправо. Для нормализации результата сдвинем мантиссу суммы на один разряд влево, а значение порядка суммы уменьшим на 1.
Окончательно 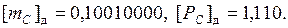
В прямом коде результат сложения запишется следующим образом:

Большое количество примеров сложения двоичных чисел с плавающей запятой можно найти в [5].
Дата добавления: 2014-12-27; просмотров: 2481;