Округление прямых кодов

Известны различные способы округления чисел в ЭВМ. Все они предполагают, что для округления числа до n разрядов необходимо вычислять разрядов округляемого числа, где .

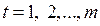Различают три вида округления:

1. Округление к нулю, когда число, т.е. правильная дробь, округляется до ближайшего к нулю машинного числа.

2. Округление от нуля, когда число округляется до машинного числа, лежащего дальше от нуля, чем округляемое число.

3. Округление по дополнению, когда округление производится до ближайшего машинного числа.

Рассмотрим несколько методов округления и дадим для них оценку погрешности.

Округление к нулю выполняется методом усечения, который заключается в отбрасывании t избыточных разрядов числа. Такой метод округления наиболее прост в реализации и не требует дополнительного времени выполнения. В этом случае максимальная величина модуля погрешности (для двоичной правильной дроби) определяется выражением

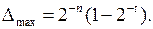
Если появление чисел с разными знаками равновероятно и всевозможные двоичные комбинации дополнительных разрядов числа также равновероятны, математическое ожидание погрешности округления для метода усечения равно нулю. Если же появление чисел с разными знаками не равновероятно, математическое ожидание погрешности округления методом усечения запишется как

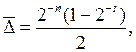
т.е. при действиях с числами одного знака будет иметь место систематическое накопление погрешности округления.

Округление от нуля предполагает анализ избыточных разрядов на равенство нулю, при этом избыточная часть отбрасывается и, если отбрасываемая часть не равна нулю, в младший разряд оставшейся части добавляется единица.

Основные характеристики этого метода округления полностью совпадают с характеристиками метода усечения. При этом округление от нуля требует использования дополнительного времени и схемотехнических ресурсов для анализа избыточных разрядов, а также для формирования распространения переносов при добавлении единицы в младший разряд округляемого числа, поэтому использование метода округления от нуля невыгодно.

Округление по дополнению представляет собой комбинацию двух предыдущих методов и заключается в том, что к младшему разряду сохраняемой части числа (двоичной правильной дроби) прибавляется некоторая величина aÎ{0,1}, определяемая по старшей цифре избыточной части числа. Если 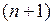-й разряд числа содержит единицу, то после отбрасывания избыточной части к младшему разряду сохраняемой части числа добавляется единица, т.е. . В противном случае к младшему разряду сохраняемой части добавляется нуль. Для простоты реализации можно не выполнять анализ дополнительного 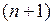-го разряда, а всегда прибавлять единицу округления в 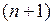-й разряд. Если в нем содержится единица, то будет сформирован перенос в младший разряд сохраняемой части, что эквивалентно прибавлению .

При таком методе округления значение максимума погрешности составляет

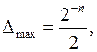
а математическое ожидание погрешности округления (в случае равновероятного появления как чисел с разными знаками, так и нулей и единиц в отбрасываемой части числа) равно нулю. Если появление чисел разного знака не равновероятно, как часто бывает при выполнении различных вычислений, то математическое ожидание погрешности округления не равно нулю и поэтому возможны систематические ошибки округления. Однако эти ошибки меньше, чем при усечении, поэтому в дальнейшем будем использовать метод округления по дополнению, если не оговорено иное.

Метод округления по дополнению имеет ряд модификаций для устранения имеющихся недостатков. Так, например, систематические ошибки округления сводятся к нулю, если решение о коррекции сохраняемой части принимается на основании анализа не одного дополнительного разряда, а всей отсекаемой части. Такой метод носит название усовершенствованного округления по дополнению. Однако он не лишен недостатков, связанных с временными и аппаратурными затратами на анализ отбрасываемой части числа и распространение переноса, поэтому его применение целесообразно в вычислительных устройствах, требующих повышенной точности вычислений.

Для устранения сложностей с распространением переноса используется так называемый метод упрощенного округления по дополнению. Его суть заключается в том, что младший разряд сохраняемой части устанавливается равным единице в том случае, когда старший дополнительный разряд равен единице. В противном случае коррекция не выполняется. При этом, если в неокругленном числе младший разряд сохраняемой части равен единице, его значение не изменяется.

Если в неокругленном числе младший разряд сохраняемой части равен нулю, то максимальная погрешность округления при установке его в единицу может составить

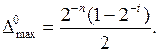
В противном случае максимальная погрешность составит

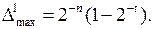
При равновероятном появлении нуля и единицы в младшем разряде сохраняемой части для знакопеременных чисел значение математического ожидания погрешности равно нулю.

Метод упрощенного округления по дополнению в общем случае имеет математическое ожидание погрешности округления, отличное от нуля. Однако в том случае, когда число избыточных разрядов 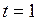, округление происходит без накопления систематических ошибок.