Двоично-десятичные коды чисел

Исходя из вышеизложенного, можно заключить, что создание универсальных цифровых вычислительных устройств, функционирующих в наиболее удобной для человека десятичной системе представления чисел (квантование сигналов осуществляется по десяти уровням), не является рациональным, поскольку характеристики десятичных схем уступают по некоторым параметрам характеристикам двоичных схем. Поэтому в ряде случаев для синтеза десятичных вычислительных устройств используют двоично-десятичное представление чисел, т.е. кодирование десятичных цифр комбинациями двоичных.

Очевидно, что кодирование десятичных цифр комбинациями двоичных цифр может быть осуществлено различными способами. При этом должно выполняться условие единственности, т.е. в выбранной системе кодов каждому десятичному числу ставится в соответствие единственная комбинация двоичных цифр и наоборот. Для этого число разрядов двоичного кода должно удовлетворять условию 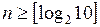, где квадратные скобки означают округление до большего целого, т.е. . 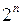Если учесть, что при переборе различных систем кодирования любой десятичной цифре можно поставить в соответствие любое из n-разрядных двоичных чисел, то число способов кодирования определяется как

,

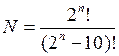т.е. как число размещений из 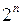по 10, поскольку эти соединения элементов отличаются друг от друга самими элементами или их порядком.

Из соображений минимизации наибольшее распространение получили двоично-десятичные коды, в которых десятичные цифры кодируются четырехразрядными двоичными комбинациями (двоичными тетрадами), т.е. 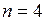. Отсюда число способов кодирования . Известны также и другие коды с числом разрядов .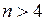

Среди такого большого числа кодов наибольшее распространение вследствие своей эффективности и изученности получили коды, удовлетворяющие условию единственности и обладающие свойствами аддитивности, упорядоченности, четности, самодополняемости и взвешенности.

Свойство аддитивности заключается в том, что код суммы десятичных цифр может быть получен как сумма кодов слагаемых.

Упорядоченность двоично-десятичных кодов определяется выполнением одного из условий:

,

,

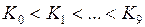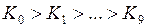где 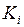– двоично-десятичный код i-й десятичной цифры.

Свойство четности заключается в том, что всем четным десятичным цифрам должны соответствовать только четные или только нечетные коды (аналогично для нечетных десятичных цифр).

Свойство самодополняемости кратко рассмотрено в разделе 1.1 и заключается в том, что сумма двоичного кода любой десятичной цифры и ее обратного двоично-десятичного кода должна быть равна двоично-десятичному коду цифры 9.

Свойством взвешенности обладают такие коды, в которых каждая десятичная цифра X может быть представлена полиномом вида

,

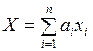где 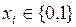– двоичные цифры кода; 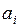– некоторые веса, соответствующие разрядам двоичных кодовых комбинаций.

В табл. 1.3 представлены некоторые двоично-десятичные коды ( 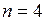) десятичных цифр.

Таблица 1.3

Код 8421 по сути является простейшим D-кодом с естественным порядком весов, т.е. в двоичной тетраде старший разряд имеет наибольший вес – 8 ( ), а младший разряд – наименьший вес – 1 ( 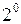). Этот код обладает свойствами аддитивности, упорядоченности, четности и взвешенности, однако, как указывалось выше, не обладает свойством самодополняемости. Для получения обратного кода необходимо увеличить значения, записанные в каждой тетраде числа на 6, т.е. преобразовать код 8421 в код 8421 с избытком 6 (8421+6), а затем инвертировать двоичные разряды.

Код 8421 с потетрадным избытком 3 (8421+3) обладает свойством самодополняемости, поэтому для получения обратного кода отрицательного числа достаточно просто инвертировать двоичные разряды в тет­радах.

Коды 2421 и 3321 являются кодами с искусственным порядком весов. В таких кодах некоторые десятичные цифры могут быть представлены несколькими кодовыми комбинациями. Для выполнения условия единственности некоторые разрешенные кодовые комбинации считают запрещенными.

Подробнее об арифметике двоично-десятичных кодов см. в разде­- ле 2.7.

Вопросы для самоконтроля

1. Что такое позиционные системы счисления и в чем их отличие от непозиционных? Какие позиционные системы счисления вам известны?

2. Какие способы представления чисел в ЦВМ вам известны? В чем заключаются особенности представления чисел с фиксированной запятой?

3. В чем заключаются особенности представления чисел с плавающей запятой?

4. Какие инверсные коды чисел вам известны? Как они образуются и в чем их отличие от прямого кода?

5. Что такое двоично-десятичные коды чисел? Какие двоично-десятичные коды получили наибольшее распространение в цифровой вычислительной технике? Какими свойствами они характеризуются?

2. Арифметические операции
в двоичных кодах