ТЕМА II. СИЛЫ ИНЕРЦИИ
Орбита космического аппарата (рис. 2.7) – это его путь в поле центральной силы, определяемый воздействием силы тяготения, при этом сам космический аппарат считается бесконечно малым телом, масса которого настолько мала по сравнению с массой центрального тела, что его можно считать притягиваемым центральным телом, но не притягивающим последнее. Поле притягивающей силы определяют обычно как поле тяготения, создаваемое однородным и сферическим телом. Применительно к ИСЗ таким телом является Земля с ее полем тяготения.
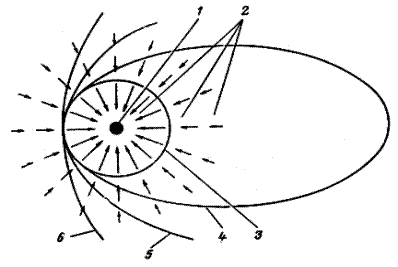
Рис. 2.7. Орбиты космического аппарата в поле центрального тела:
1 — центральное тело;
2— силовое поле центрального тела;
3— круговая орбита;
4 — эллиптическая орбита;
5 — параболическая орбита; 6— гиперболическая орбита
Силовое поле центральной силы сферически симметрично и сила притяжения в каждой его точке направлена по радиусу к центру притяжения (рис. 2.7 величина стрелок показывает увеличение силы тяготения при приближении к центру массы центрального тела по закону, обратно пропорциональному квадрату расстояния).
 Из материала лекции 1 нам известно, что тело, движущееся по орбите вокруг другого тела, подчинено трём законам Кеплера. В данном случае нас будут интересовать только два из них – первый и третий.
Из материала лекции 1 нам известно, что тело, движущееся по орбите вокруг другого тела, подчинено трём законам Кеплера. В данном случае нас будут интересовать только два из них – первый и третий.
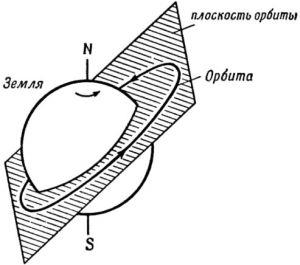
Согласно первому закону Кеплера, тело, обращающееся вокруг Земли (в нашем случае) движется по эллипсу, в одном из фокусов которого находится центр Земли (рис. 2.8). Мы специально не упоминали тут, что тело может двигаться по трём видам орбит – эллипс, гипербола и парабола. Нас интересуют только периодические орбиты, а из перечисленных такой является эллипс.
Рис. 2.8. Орбита ИСЗ
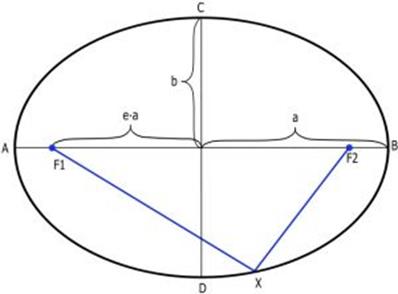 Элементы эллипса показаны на рис. 2.9. F1 и F2 – фокусы эллипса; a – большая полуось; b – малая полуось; е – эксцентриситет эллипса, который определяется следующим образом:
Элементы эллипса показаны на рис. 2.9. F1 и F2 – фокусы эллипса; a – большая полуось; b – малая полуось; е – эксцентриситет эллипса, который определяется следующим образом:
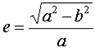
Таким образом, первое важное положение – ИСЗ движутся вокруг Земли по эллипсам.
Согласно третьему закону Кеплера, квадраты периодов обращения T спутников относятся как кубы их больших полуосей
a:
Рис. 2.9. Элементы эллипса
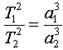
В наиболее общем случае уравнение траектории движения КА является уравнением движения свободного тела в поле центральной силы, которое в полярных координатах имеет вид уравнения конического сечения (рис. 2.10):
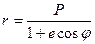 , (2.1)
, (2.1)
где 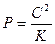 – параметр конического сечения;
– параметр конического сечения;
e =PC1 – эксцентриситет конического сечения;
С и С1 – постоянные интегрирования.
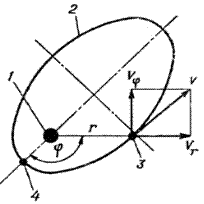
Рис. 2.10. Движение КА в поле центральной силы Земли:
1 — центральное тело (Земля); 2 — орбита КА;
3 — КА; 4 — перигей орбиты; r — радиус-вектор КА;
V — суммарная скорость; Vr — радиальная скорость;
Vφ — трансверсальная скорость
Уравнение (2.1) является уравнением кривой второго порядка, для которого конкретная форма определяется значением эксцентриситета е = 0 для окружности, е < 1для эллипса (рис. 2.11), е = 1 для параболы, е > 1 для гиперболы.
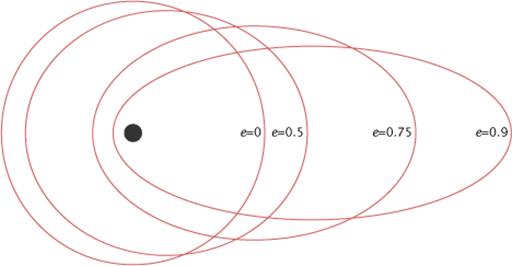
Рис. 2.11. Изменение вида эллиптической орбиты при увеличении значения
эксцентриситета
Завершающей стадией полета ракеты-носителя является вывод КА на орбиту, форма которой определяется величиной кинетической энергии, сообщаемой космическому аппарату ракетой-носителем, т. е. величиной конечной скорости последней. При этом величина кинетической энергии сообщаемой КА, должна находиться в определенном отношении к величине энергии поля центрального тела, которая существует на данном расстоянии r от его центра. Это отношение характеризуется постоянной энергии h,представляющей разность энергии поля центрального тела и кинетической энергии космического аппарата, находящегося в свободном движении в этом поле на расстоянии r от его центра, т. е.

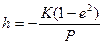 . (2.2)
. (2.2)
В зависимости от величины эксцентриситета е постоянная 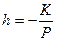 для окружности, h < 0 для эллипса, h = 0 для параболы и h > 0 для гиперболы.
для окружности, h < 0 для эллипса, h = 0 для параболы и h > 0 для гиперболы.
Конечная скорость ракеты-носителя, обеспечивающая выведение космического аппарата на орбиту в поле земного тяготения,
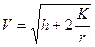 . (2.3)
. (2.3)
Анализ величин постоянной энергии h, соответствующих различным формам орбиты космического аппарата, и зависимости (2.3) позволяет установить значения конечных скоростей ракеты-носителя, обеспечивающих полет КА в поле земного тяготения по той или иной орбите.
Конечная скорость РН должна быть равна 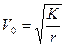 для выведения КА на круговую орбиту,
для выведения КА на круговую орбиту, 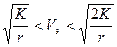 — на эллиптическую,
— на эллиптическую, 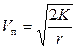 — на параболическую и
— на параболическую и 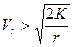 — на гиперболическую.
— на гиперболическую.
Применительно к круговым орбитам со значениями r,близкими к радиусу Земли R = 6 371 км, конечная скорость ракеты-носителя для выведения космическою аппарата на круговую орбиту V0 ~ 7900 м/с. Это так называемая первая космическая скорость. Для эллиптических орбит конечные скорости Vэ = 7 900 … 11 200 м/с.
Космические аппараты, движущиеся по круговым и эллиптическим орбитам, находятся в поле земного тяготения и имеют ограниченное время существования. Наличие остатков атмосферы и прочих частиц материи приводит со временем к уменьшению скорости космических аппаратов, сообщенной им ракетой-носителем, а торможение в силовом поле Земли вызывает их вход в плотные слои атмосферы и разрушение. Основным фактором, определяющим время жизни КА на круговой и эллиптической орбитах, является высота первой и высота перигея второй, где происходит основное торможение.
Полет космического аппарата по параболе с энергетической точки зрения характеризуется так называемой второй космической скоростью, равной Vп ≈ 11 200 м/с, которая позволяет преодолеть земное притяжение. Движение по параболе относительно Земли возможно только в случае отсутствия любых сил воздействия, кроме силы земного тяготения.
Гиперболические орбиты характеризуются скоростями Vг > 11 200 м/с, среди которых представляет интерес так называемая третья космическая скорость, равная Vг ≈ 16 700 м/с, — наименьшая начальная скорость, при которой КА может преодолеть не только земное, но и солнечное притяжение и покинуть Солнечную систему.
Гиперболические орбиты в теории космических полетов имеют место при переходе космического аппарата из поля тяготения одного центрального тела в поле тяготения другого, при этом космический аппарат как бы вырывается из одной гравитационной зоны и входит в другую.
Как правило, РН сообщают космическому аппарату только первую космическую скорость и выводят его или на круговую, или на эллиптическую орбиту. Достижение второй и третьей космических скоростей более выгодно за счет энергетики самого КА, стартующего в этом случае с опорной орбиты ИСЗ.
ТЕМА II. СИЛЫ ИНЕРЦИИ
Эта тема будет посвящена рассмотрению особого вида сил – сил инерции. Особенность этих сил состоит в следующем. Все механические силы – будь то силы гравитационного, упругого взаимодействия или силы трения – возникают тогда, когда на тело имеет место воздействие со стороны других тел. С силами инерции дело обстоит иначе.
Для начала вспомним, что такое инерция. Инерция – это физическое явление, состоящее в том, что тело всегда стремится сохранить свою первоначальную скорость. И силы инерции возникают тогда, когда у тела изменяется скорость – т.е. появляется ускорение. В зависимости от того, в каком движении принимает участие тело, у него возникает то или иное ускорение, и оно порождает ту или иную силу инерции. Но все эти силы объединяет одна и та же закономерность: сила инерции всегда направлена противоположно ускорению ее породившему.
По своей природе силы инерции отличаются от других механических сил. Все остальные механические силы возникают в результате воздействия одного тела на другое. Тогда как силы инерции обусловлены свойствами механического движения тела. Кстати, в зависимости от того, в каком движении участвует тело, возникает та или иная сила инерции:
• движение может быть прямолинейным, и тогда речь пойдет о силе инерции поступательного движения;
• движение может быть криволинейным, и тогда речь пойдет о центробежной силе инерции;
• наконец, движение может быть одновременно и прямо-, и криволинейным (если тело перемещается во вращающейся системе или перемещается, вращаясь), и тогда речь пойдет о силе Кориолиса.
Рассмотрим подробнее виды сил инерции и условия их возникновения.
1. СИЛА ИНЕРЦИИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯFi. Она возникает, когда тело движется по прямолинейной траектории. Мы постоянно сталкиваемся с действием этой силы в транспорте, движущемся по прямой дороге, при торможении и при наборе скорости. При торможении нас бросает вперед, т.к. скорость движения резко уменьшается, а наше тело старается сохранить ту скорость, которая у него была. При наборе скорости нас вдавливает в спинку сидения по той же причине. На рис. 2.1
Рис. 2.1
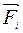
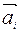

























Изображены направления ускорения и силы инерции поступательного движения в случае уменьшения скорости: ускорение 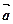 направлено противоположно движению, а сила инерции
направлено противоположно движению, а сила инерции 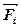 направлена противоположно ускорению. Формула силы инерции задается вторым законом Ньютона:
направлена противоположно ускорению. Формула силы инерции задается вторым законом Ньютона: 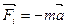 . Знак «минус» обусловлен тем, что векторы
. Знак «минус» обусловлен тем, что векторы 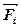 и
и 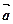 имеют противоположные направления. Численное значение (модуль) этой силы соответственно вычисляется по формуле:
имеют противоположные направления. Численное значение (модуль) этой силы соответственно вычисляется по формуле:
 F = ma (3.1)
F = ma (3.1)
2. ЦЕНТРОБЕЖНАЯ СИЛА ИНЕРЦИИFi. Чтобы понять, как возникает эта сила, рассмотрим рис. 3.2, на котором изображен диск, вращающийся в горизонтальной плоскости, с шариком, прикрепленным к центру диска посредством растяжимой связи (например, резинки). Когда диск начинает вращаться, шарик стремится удалиться от

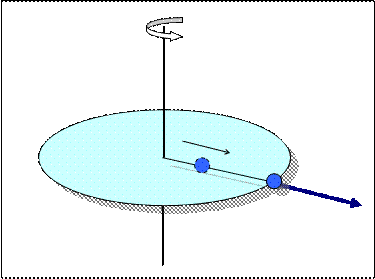
Рис. 3.2
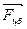
центра и натягивает резинку. Причем чем быстрее вращается диск, тем дальше удаляется шарик от центра диска. Такое перемещение шарика по плоскости диска обусловлено действием силы, которая называется центробежной силой инерции (Fцб). Таким образом, центробежная сила возникает при вращении и направлена вдоль радиуса от центра вращения.Fцб является силой инерции, а значит ее возникновение обусловлено наличием ускорения, которое должно быть направлено противоположно этой силе. Если центробежная сила направлена от центра, то очевидно, что причиной возникновения этой силы является нормальное (центростремительное) ускорение аn, ведь именно оно направлено к центру вращения (см. Тема 1, §1.2, п.3). Исходя из этого, получаем формулу центробежной силы. Согласно второму закону Ньютона F=ma, где m – масса тела. Тогда для центробежной силы инерции справедливо соотношение:
 Fцб = man.
Fцб = man.
Учитывая (1.18) и (1.19), получаем:
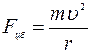 (3.2) и Fцб = mω2r (3.3).
(3.2) и Fцб = mω2r (3.3).
3. СИЛА КОРИОЛИСА FK. При совмещении двух видов движения: вращательного и поступательного – появляется еще одна сила, называемая силой Кориолиса (или кориолисовой силой) по имени французского механика Густава Гаспара Кориолиса (1792-1843), который дал расчет этой силы.
Появление кориолисовой силы можно обнаружить на примере опыта, изображенного на рис. 3.3. Ни нем изображен диск, вращающийся в горизонтальной
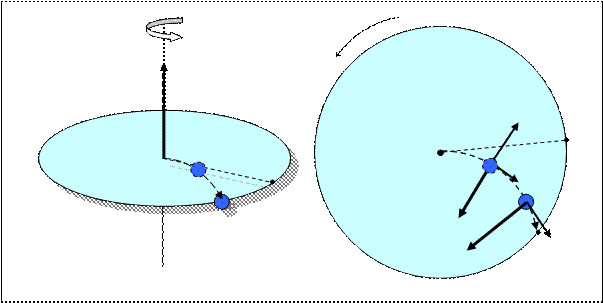
Рис. 3.3 вид сверху
а). 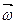
 б).
б).
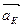
А
О О 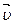
А 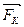
В 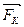 В
В 
плоскости. Прочертим на диске радиальную прямую ОА и запустим в направлении от О к А шарик со скоростью υ. Если диск не вращается, шарик будет катиться вдоль прочерченной нами прямой. Если же диск привести во вращение в направлении, указанном стрелкой, то шарик будет катиться вдоль изображенной пунктиром кривой ОВ, причем его скорость υ будет изменять свое направление (см. рис.3.3 (б)). Следовательно, по отношению ко вращающейся системе отсчета (а в данном случае это диск) шарик ведет себя так, как если бы на него действовала некая сила, перпендикулярная скорости υ. Это и есть сила Кориолиса FK. Именно она заставляет шарик отклоняться от прямолинейной траектории ОА. Формула, которая описывает эту силу определяется опять же вторым законом Ньютона, только на этот раз в качестве ускорения выступает так называемое кориолисово ускорениеаК: 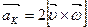 ,
,
где: υ – линейная скорость тела относительно вращающейся системы отсчета,
ω – угловая скорость вращения системы (в нашем случае она направлена вертикально
вверх (см. рис.3.3 (а)),
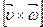 - векторное произведение векторов
- векторное произведение векторов 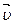 и
и 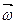 .
.
Здесь уместно было бы вспомнить, что такое векторное произведение. Векторным произведением двух векторов является вектор, перпендикулярный плоскости, содержащей эти вектора, и равный произведению их модулей на синус угла между ними: 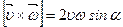 , где α - угол между векторами
, где α - угол между векторами 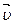 и
и 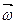 .
.
Таким образом, мы получаем формулу для силы Кориолиса:
FK=2mυωsinα (3.4).
Если α = 90º, то sinα= 1, следовательно: FK=2mυω (3.5).
Итак, как уже было сказано, чтобы сила Кориолиса проявила себя, необходимо совместить 2 вида движения. И здесь возможны два варианта: 1). Тело движется относительно вращающейся системы отсчета. Именно этот случай изображен на рис.3.3. 2). Вращающееся тело совершает поступательное движение В качестве примера можно рассматривать так называемые «крученые» мячи – прием, используемый в футболе – когда удар по мячу осуществляется так, что он во время полета вращается.
Дата добавления: 2014-12-26; просмотров: 1354;
