Обчислення видимих координат Сонця за доп астроном щорічника.

α=α₀+hv_a

δ=δ₀+hv_a

h=T_n+1-(n+1)+∆T
Va(δ)=Va0(δ0)+h(Va1(δ1)-Va0(δ0)/48
Va0(a1)=9.856s/h-Ve0(e1)
T0=m-λ
T0*=T0+∆T
h=(T0)*

18 Обчислення корд зірок за доп астроном щорічника
α=α₀+hv_a

δ=δ₀+hv_a

h=0.1(d+T^d)
T^d=(S-a)/24
T^d=-(a-S)/24
T^d=(s-λ-s₀)*0.99727/24

S=s-λ

19Видимий річний рух сонця і його вплив на істинний часЗемля як планета здійснює в просторі два види руху: обертаючись, як небесне тіло, навколо своєї осі; обертаючись, як небесне тіло, по орбіті довкруги Сонця.

Перший вид руху – обертання довкола своєї осі відображається видимим переміщенням зірок по небесній сфері. Траєкторією такого руху є добові паралелі зірок. Оскільки Сонце також є зіркою, то його видимий добовий рух описується добовою паралеллю з точками кульмінації, коли Сонце перетинає меридіан точки спостереження. Якщо вважати, що обертання Землі є рівномірним, то і видимий добовий рух Сонця по добовій паралелі буде проходити з рівномірною швидкістю.

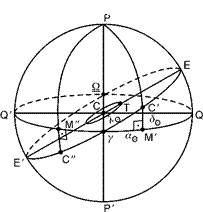
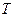На основі першого закону Кеплера руху планет встановлюємо вид орбіти Землі, яким є еліпс, тобто Земля обертається довкола Сонця по еліпсу. Продовживши площину еліпса орбіти а точніше площину орбіти спільного центра маси Землі і Місяця до перетину з небесною сферою, отримаємо площину екліптики небесної сфери (рис. 3.2). В цілій площині будуть знаходитись і Земля - , і Сонце - 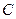. 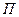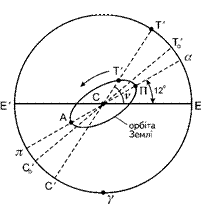Рух Землі по орбіті описується другим законом Каплера, і він відбувається з нерівномірною швидкістю: з більшою швидкістю Земля рухається по орбіті в районі точки перигелія і з меншою швидкістю в районі точки афелія 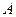(рис. 3.3). Точкам перигелія і афелія на орбіті Землі будуть відповідати точки перигея 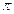і апогея 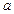на екліптиці.

Рисунок 3.2 - До видимого річного руху Сонця	Рисунок 3.3 - Видимий річний рух Сонця

Оскільки лінія апсид 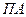складає з напрямом лінії сонцестоянь кут близький до 12˚, то точка перигея 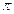буде розміщена на екліптиці ближче до точки зимового сонцестояння 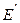, а точка апогея 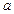- ближче до точки літнього сонцестояння .

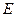Видимий річний рух Сонця по екліптиці є відображен-ням дійсного річного руху Землі по орбіті навколо Сонця. Дійсно, рухаючись разом з Землею, спостерігач якби проектує Сонце в той чи інший момент року на коло екліптики небесної сфери. Так, знаходячись разом з Землею в точці перигелію 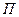, ми бачимо Сонце в точці перигея 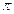екліптики, а, наприклад, при знаходженні Землі в точці орбіти 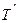будемо спостерігати Сонце в точці 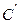(рис. 3.3). Оскільки Земля по своїй орбіті рухається з різною швидкістю (другий закон Каплера), то і видимий рух Сонця по екліптиці буде проходити з різною швидкістю: з максимальною в районі точки перигея 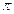і з мінімальною – в районі точки апогея .

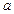За рік Земля робить один повний оберт по орбіті довкола Сонця. Відповідно видиме Сонце повинно за рік обійти коло екліптики, тому кожен день зміщення Сонця на екліптиці становить 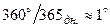, або приблизно 4 хвилини за часом.

У своєму видимому русі по екліптиці Сонце проходить через її чотири характерні точки: точку весняного рівнодення, точку літнього сонцестояння, точку осіннього рівнодення, точку зимового сонцестояння. Причому цей рух здійснюється в тому ж напрямі, що і рух землі по орбіті, тобто проти ходу годинникової стрілки.

Для визначення положення видимого Сонця на екліптиці найчастіше використовують дві системи координат: екліптичну і другу-екваторіальну. Проаналізуємо зміну цих координат при переміщенні Сонця по екліптиці (табл. 3.1)

Таблиця 3.1 - Значення координат Сонця в точках екліптики

Позначення точки екліптики	Дата за календарем і назва точки	Координати	Співвідношення
екліптичні	екваторіальні
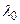
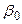
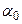
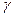
	21 березня, точка весняного рівнодення	0h	0°	0h	0°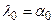
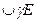
І квадрант	Астрономічна весна	-	-	-	зрост.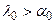
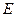
	22 червня, день літнього сонцестояння	6h	0°	6h	+23.5º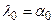
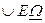
ІІ квадрант	Астрономічне літо	-	-	-	зменш.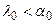
	23 вересня, день осіннього рівнодення	12h	0°	12h	00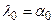
ІІІ квадрант	Астрономічна осінь	-	-	-	зменш.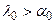
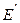
	22 грудня, день зимового сонцестояння	18h	0°	18h	-23.5°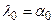
ІV квадрант	Астрономічна зима	-	-	-	зрост.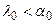

Проведемо аналіз координат, наведених в таблиці 3.1. Розглянемо прямокутний сферичний трикутник 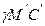(рис. 3.1), в якому 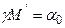- катет трикутника, а - гіпотенуза трикутника. Оскільки , то і .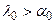

Ця закономірність буде справедливою у всіх точках екліптики І і ІІІ квадрантів. Для точок IV квадранту (наприклад 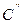) екліптична довгота 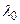буде відповідати сферичній відстані 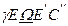, тобто 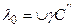. Пряма сходження 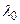Сонця в точці 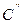відповідає сферичній відстані 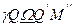, тобто . Оскільки в сферичному трикутнику 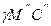сторона 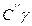є гіпотенузою, а сторона 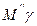- катетом і відповідн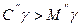о , то 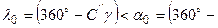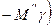. Така ж залежність буде і в другому квадранті.

Розглянуті залежності між 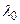і 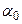свідчать про те, що нахил екліптики до екватора спричинює їх нерівність, а також різний характер залежності між ними. Необхідно звернути увагу і на те, що різна швидкість руху видимого Сонця по екліптиці зумовлює і різну тривалість певних періодів року. Так, видимий рух Сонця по екліптиці на ділянці від точки осіннього рівнодення до точки весняного рівнодення 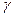(дуга 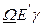) відповідає осінньо-зимовому періоду року. На цій ділянці екліптики швидкість руху видимого Сонця буде більшою, ніж на ділянці 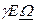, що відповідає весняно-літньому періоду, оскільки максимальна швидкість буде в точці перигею 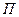. Тому в північній півкулі Землі осінньо-зимовий період року приблизно на вісім діб коротший за весняно-літній період.