Изотермический процесс.

При изотер­мическом процессе температура постоян­на, следовательно,

рV = RТ = сопst, или p₂/p₁ = υ₁/υ₂ [49]

т. е. давление и объем обратно пропорци­ональны друг другу, так что при изо­термическом сжатии давление газа воз­растает, а при расширении — падает (закон Бойля — Мариотта, 1662г.).

Графиком изотермического процесса в р,V - координатах, как показывает урав­нение (4.12), является разнобокая гипербола, для которой координатные оси служат асимптотами (рис. 16).

Работа процесса

l = 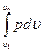= 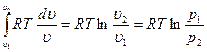[50]

Так как температура не меняется, то внутренняя энергия идеального газа в данном процессе остается постоянной (Δu = 0) и вся подводимая к газу тепло­та полностью превращается в работу расширения: q = l

При изотермическом сжатии от газа от­водится теплота в количестве, равном затраченной на сжатие работе.

Из соотношений 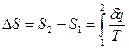и [49] следу­ет, что изменение энтропии в изотермиче­ском процессе выражается формулой

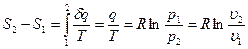[51]

Адиабатный процесс. Процесс, про­исходящий без теплообмена с окружаю­щей средой, называется адиабатным, т. е. δq = 0. Для того чтобы осуществить та­кой процесс, следует либо теплоизолиро­вать газ, т. е. поместить его в адиабат­ную оболочку, либо провести процесс на­столько быстро, чтобы изменение темпе­ратуры газа, обусловленное его тепло­обменом с окружающей средой, было пренебрежимо мало по сравнению с из­менением температуры, вызванным рас­ширением или сжатием газа. Как прави­ло, это возможно, ибо теплообмен про­исходит значительно медленнее, чем сжатие или расширение газа.

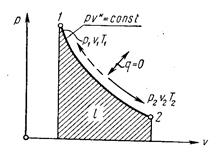Уравнения первого закона термоди­намика для адиабатного процесса прини­мают вид:

c_pdT - υdp = 0; c_υdT + pdυ = 0 Поделив первое уравнение на второе, получим

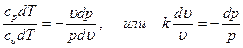
Интегрируя последнее уравнение при условии, что k = с_р/c_υ = const , находим

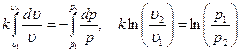После потенцирования имеем или

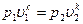[52]

Это и есть уравнения адиабаты идеаль­ного газа при постоянном отношении теплоемкостей (k = const).

Величина k = c_p/c_υ [53]

называется показателем адиаба­ты. Подставив c_p = c_υ + R, получим k = 1 + R/c_υ Согласно классической кине­тической теории теплоемкость газов не зависит от температуры по­этому можно считать, что величина k также не зависит от температуры и оп­ределяется числом степеней свободы мо­лекулы. Для одноатомного газа k =1,66, для двухатомного k =1,4, для трех-и многоатомных газов k =1,33.

Поскольку k > 1, то в координатах р, υ (рис. 4.4) линия адиабаты идет круче линии изотермы: при адиабатном расши­рении давление понижается быстрее, чем при изотермическом, так как в процессе расширения уменьшается температура газа.

Определив из уравнения состояния, написанного для состояний 1 и 2, отно­шение объемов или давлений и подста­вив их в [52], получим уравнение адиа­батного процесса, устанавливающего связь между р и υ; υ и Т; р и Т и термическим уравнением состояния для этих же точек p₁υ₁ =RT₁ p₂υ₂ = RT₂ или 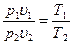В результате несложных математических преобразований получим

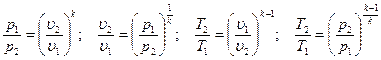[54]

Из первого закона термодинамики при q = 0 для адиабатного процесса следует Δu +l =0 тогда l = -Δu = c_υ ^. (T₁-T₂) = 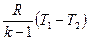(Теплоемкость адиабатного процесса также равна нулю).

Следовательно, работа расширения при адиабатном процессе согласно первому закону термодинамики совершается за счет уменьшения внутренней энергии газа. В обратном процессе сжатия работа, совершаемая внешней средой над газом, идет на увеличение внутренней энергии газа, на повышение его температуры.

так как p₁υ₁ =RT₁ p₂υ₂ = RT₂ то 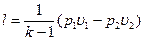[55]

Еще раз повторим, что в данном процессе теплообмен газа с окружающей средой исключается, по­этому δq = 0. Выражение с=δq/Tпока­зывает, что теплоемкость адиабатного процесса также равна нулю.

Поскольку при адиабатном процессе δq = 0, энтропия рабочего тела неизме­няется (ds = 0, s = const). Следователь­но, на Т, S-диаграмме адиабатный про­цесс изображается вертикалью.

Политропный процесс и его обобща­ющее значение.Любой произвольный процесс можно описать в р, v-координатах (по крайней мере на небольшом участке) уравнением подбирая соответствующее значение п.

pυⁿ = const, [56]

Процесс, описываемый уравнением pυⁿ = const, называется политропным (от греческих слов поли- много и тропос-путь, направление). Показатель политропы п может прини­мать любое численное значение в преде­лах от 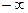до 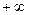, но для данного процесса он является величиной посто­янной.

pυⁿ = const,

Описанные четыре основных процесса можно рассматривать как частные случаи политропного процесса. Действительно, при n = 0 уравнение политропы приобретает вид рυⁿ = pυ⁰ = р = сonst, получаем уравнениеизобары.

При n = 1 рυⁿ = pυ = сonst, имеем уравнение изотермы

При n = k рυⁿ = pυ^k = сonst, - уравнение адиабаты.

Извлекая из обеих частей уравнения рυⁿ = сonst, корень n-й степени и приравнивая 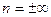, получаем 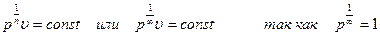то получаем уравнение υ = сonst, т. е. уравнение изохоры.

Из уравнения (4.21) и уравнения Клапейрона нетрудно получить выраже­ния, устанавливающие связь между р, υи Т в любых двух точках наполитропе, аналогично тому, как это было сделано для адиабаты:

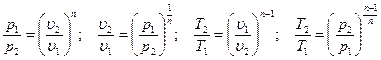[57]

Работа расширения газа в политропном процессе имеет вид l=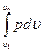

так как для политропы в соответст­вии с [57] 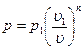то

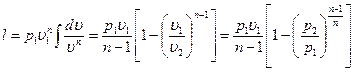[58]

Преобразуем эти уравнения к виду

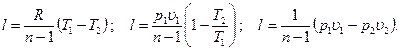[59]

Количество подведенной (или отве­денной) в процессе теплоты можно опре­делить с помощью уравнения первого закона термодинамики: q = (u₂ – u₁) + l так как

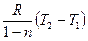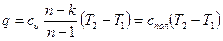u₂ – u₁ = с_υ(Т ₂-Т₁), l= то [60]

где с_пол = 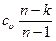представляет собой теплоемкость иде­ального газа в политропном процессе. При постоянных c_υ, и и п теплоемкость с_пол= соnst, поэтому политропный процесс иногда определяют как процесс с посто­янной теплоемкостью.

Изменение энтропии при политропном процессе найдем из формулы:

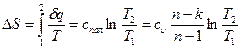.[61]