В ЗАКРЫТЫХ СИСТЕМАХ
Основными процессами, весьма важными и в теоретическом, и в прикладном отношениях, являются: изохорный, протекающий при постоянном объеме; изобарный, протекающий при постоянном давлении; изотермический, происходящий при постоянной температуре; адиабатный — процесс, при котором отсутствует теплообмен с окружающей средой, и политропный, удовлетворяющий уравнению рvn = соnst.
Метод исследования процессов, не зависящий от их особенностей и являющийся общим, состоит в следующем:
выводится уравнение процесса, устанавливающее связь между начальными и конечными параметрами рабочего тела в данном процессе;
вычисляется работа изменения объема газа;
определяется количество теплоты, подведенной (или отведенной) к газу в процессе;
определяется изменение внутренней энергии системы в процессе;
определяется изменение энтропии системы в процессе.
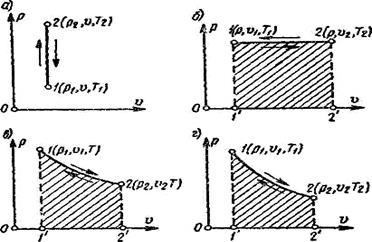
|
| Рис.13 а-изохорный, б- изобарный в-изотермический, г- адиабатный |
Изохорный процесс. При изохорном процессе выполняется условие
dυ = 0 или υ = const.
Из уравнения состояния идеального газа (1.3) следует, что P/T = R/V = const, т. е. давление газа в изохорном процессе прямо пропорционально его абсолютной температуре: P2/P1 = T2/T1
Работа расширения в этом процессе равна нулю, dV = 0, так как
ΔV =V2 – V1 = 0; V1 = V2 в PV диаграмме нет площади, измеряющей работу в изохорном процессе.
Количество теплоты, подведенной к рабочему телу в процессе 1-2 при сυ = const, определяется из соотношений:
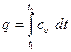 = cυ(T2 – T1)[47]
= cυ(T2 – T1)[47]
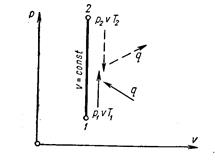
Уравнение можно выразить так: в изохорном процессе все подводимое к газу тепло идет на изменение (увеличение) его внутренней энергии, на повышение температуры; внешняя работа не совершается
|
|
qV = Δ u = u2 – u1
Δ u = q
Δu = cυ (T2 –T1), при сυ = const
Поскольку внутренняя энергия идеального газа является функцией только его температуры, то формулы (4.4) справедливы для любого термодинамического процесса идеального газа.
Изменение энтропии в изохорном процессе определяется по формуле (3.6):
S2 - S1 = cυ ln( 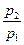 ) = cυ ln(
) = cυ ln( 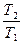 )
)
т. е. зависимость энтропии от температуры на изохоре при сυ = const имеет логарифмический характер (см. рис. 4.1).
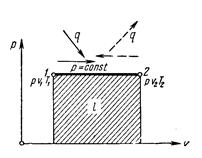 Изобарный процесс.Из уравнения состояния идеального газа pV/T = R или pV = RT при р = const находим V/T = R/p = const или V2/V1=Т2/T1 [48]
Изобарный процесс.Из уравнения состояния идеального газа pV/T = R или pV = RT при р = const находим V/T = R/p = const или V2/V1=Т2/T1 [48]
|
т. е. в изобарном процессе объем газа пропорционален его абсолютной температуре (закон Гей-Люссака, 1802г.). Работа выразится уравнением l = 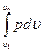 = p(V2 – V1), так как pυ1 =RT1 pυ2 = RT2
= p(V2 – V1), так как pυ1 =RT1 pυ2 = RT2
то l = R(T2 – T1)
Количество теплоты, сообщаемое газу при нагревании (или отдаваемое им при охлаждении), находим из уравнения математического выражения первого закона термодинамики: 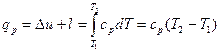 Таким образом, в изобарном процессе сообщенное газу тепло идет на увеличение его внутренней энергии и совершение внешней работы.
Таким образом, в изобарном процессе сообщенное газу тепло идет на увеличение его внутренней энергии и совершение внешней работы.
Изменение энтропии в изобарном процессе равно S2-S1 = cр ln( 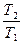 ) т.е температурная зависимость энтропии также имеет логарифмический характер но так как
) т.е температурная зависимость энтропии также имеет логарифмический характер но так как
ср >сυ, то изобара в TS –диаграмме идет более полого, чем изохора.
Дата добавления: 2014-12-24; просмотров: 1367;
