Силы, действующие на самолет в полете
Пространственное движение самолета, характеризующееся изменением положения самолета в пространстве, изменением скорости и направления полета, называется маневром, а способность совершать маневр – маневренностью самолета (франц. manoeuvrer – приводить в движение, управлять, маневрировать, от лат. manu operor – работаю руками).
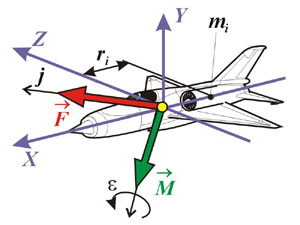
Все силы, действующие на самолет в полете, могут быть сведены к трем: полной аэродинамической силе Ra , силе тяжести G и силе тяги двигателя P . Эти силы, в свою очередь, можно привести к равнодействующей силе F, приложенной в центре масс самолета, и моменту Mотносительно центра масс (рис. 6.4):
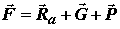
| ; | 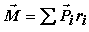
|
где
| Pi | - | составляющие силы F; |
| ri | - | плечо силы Pi относительно центра масс |
В общем случае сила F и момент M, действующие на самолет, отличны от нуля и самолет движется поступательно вдоль вектора силы F с ускорением j = F/m и вращается относительно оси, направленной вдоль вектора M с угловым ускорением
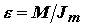
|
где
| j | - | линейное ускорение центра масс самолета, м/с2; |
| F | - | действующая на самолет сила, Н; |
| m | - | масса самолета, кг; |
| e | - | угловое ускорение самолета, рад/с2; |
| M | - | действующий на самолет момент сил, Н·м; |
| Jm | - | момент инерции самолета относительно центра масс, кг·м2. |
Момент инерции самолета относительно центра масс
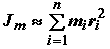
|
где
| mi | - | масса i-го агрегата самолета (например, масса двигателя); |
| ri | - | расстояние от центра масс i-го агрегата до оси вращения самолета, проходящей через центр масс, т. е. до вектора момента M. |
|
| Рис. 6.4. Силы действующие на самолет в криволинейном полете |
При ускоренном поступательном и вращательном движении самолета на каждый агрегат или размещенный на самолете груз действуют инерционные силыPi = miji , где mi – масса i-го агрегата самолета; ji– линейное ускорение i-го агрегата. В этом случае линейное ускорение каждого агрегата вследствие вращательного движения самолета будет отличаться от линейного ускорения центра масс самолета тем больше, чем дальше от центра масс самолета находится агрегат.
Движущийся в криволинейном пространственном полете самолет можно рассматривать как находящийся в равновесии, если по принципу Д'Аламбера (по имени французского математика, механика и философа Ж. Л. Д'Аламбера) включить в число действующих на него сил силу инерции
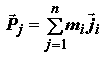
|
равную сумме инерционных сил, действующих на каждый агрегат самолета. Таким образом, можно записать:
F + Pj = 0, т.е.Ra + G + P + Pj = 0.
Все силы, действующие на самолет в полете, удобно объединить в две группы:
- поверхностные силы - силы, не связанные с массой самолета (полная аэродинамическая сила Raи сила тяги двигателя P ), которые, собственно, и определяют полет: Rп = Ra + P ;
- массовые силы – силы, связанные с массой самолета (сила тяжести G и инерционная сила Pj ), которые необходимо преодолеть для совершения полета: Rм = G + Pj.
Здесь уместно еще раз отметить, что сила лобового сопротивления Xa, которую приходится преодолевать силой тяги двигателя P, возникает как неизбежное следствие получения подъемной силы Ya, неразрывно связана с ней, поэтому силу лобового сопротивления, как и подъемную силу, с полным основанием можно отнести к группе силRп, которые определяют полет.
Таким образом, можно рассматривать равновесие самолета в любом пространственном движении под действием сил Rп и Rм, т. е.
F = Rп + Rм = 0; M = Mп + Mм= 0.
Изменение силы F и момента M(появление приращенийΔFи ΔM при изменении полной аэродинамической силы Ra, силы тяги двигателя P или силы тяжести G) приводит к изменению параметров пространственного движения самолета.Движение самолета неуправляемое, если приращения (возмущения) силы ΔFи момента ΔMне обусловлены действиями летчика, а вызваны какими- либо не зависящими от него обстоятельствами (например, порыв ветра в турбулентной атмосфере). Движение самолета управляемое, если приращение силы ΔF и момента ΔMобусловлено действиями летчика. В этом случае ΔFи ΔMназываются управляющимивоздействиями. Летчик может изменить значение и ориентацию в пространстве полной аэродинамической силы, значение и направление силы тяги двигателя. Целенаправленное изменение этих сил приведет к формированию потребной траектории полета самолета.
При решении многих задач, связанных с полетом самолета (расчет траекторий, определение прочностных характеристик и т. д.), используется понятие перегрузки.
Перегрузка– отношение суммы векторов полной аэродинамической силы и силы тяги к силе тяжести:
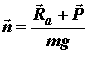
|
Поскольку Rп = Ra + Pи P = – Pм , то
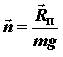
| или | 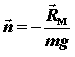
|
Вектор перегрузки характеризует маневренность самолета, так как он учитывает величину и направление сил, изменяя которые можно управлять траекторией движения самолета. Перегрузка показывает, во сколько раз силы, определяющие траекторию движения, больше или меньше силы тяжести самолета или (что то же самое) во сколько раз ускорение движения самолета в каком-либо направлении больше или меньше ускорения земного тяготения. Для каждого отдельно взятого агрегата самолета или любого груза, находящегося на самолете, перегрузка показывает, во сколько раз действующая на него сила больше или меньше силы тяжести агрегата или груза.
Перегрузка, действующая на самолет, может быть записана через ее проекции nx, ny, nz, на оси координат в виде
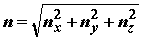
|
где
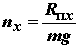
| - | продольная (тангенциальная) перегрузка; |
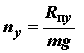
| - | нормальная перегрузка; |
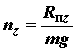
| - | боковая перегрузка; |
| Rпх, Rпу, Rпz | - | проекции силы на оси координат. |
Дата добавления: 2014-12-24; просмотров: 2145;
