Графики в трехмерном пространстве




- Построение графика функции z=f(x,y) в виде поверхности в декартовой системе координат.
- Построение графика поверхности, заданной параметрически.
- Форматирование трехмерных графиков.
- Кривая в пространстве.
- Векторные и градиентные поля.
- Поверхности, полученные вращением кривых вокруг осей.

| Построение графика функции z=f(x,y) в виде поверхности в декартовой системе координат. |
Для построения графика поверхности можно воспользоваться двумя способами:

| 1. Если вам надо только посмотреть общий вид поверхности, то MathCAD предоставляет возможность быстрого построения подобных графиков. Для этого достаточно определить функцию f(x,y) и выполнить команду Insert -> Graph -> Surface Plot или нажать соответствующую кнопку наборной панели Graph (соченание клавиш [Ctrl+7]). В появившейся графической области под осями на месте шаблона для ввода надо указать имя (без аргументов) функции. MathCAD автоматически построит график поверхности. Независимые переменные x и y принимают значения из промежутка [-5,5]. |

| При необходимости этот промежуток может быть уменьшен или увеличен. Для этого необходимо выделить график и воспользоваться командой Format -> Graph -> 3D Plot или щелкнуть ПРАВОЙ кнопкой мыши по выделенному графику и в контекстном меню выбрать команду Format. В появившемся окне 3-D Plot Format на вкладке QuickPlot Data можно установить другие параметры изменения независимых переменных x и y. |

| Для построения графика поверхности в определенной области изменения независимых переменных или с конкретным шагом их изменения необходимо сначала задать узловые точки xi и yj, в которых будут определяться значения функции. После (а можно и до) этого надо определить функцию f(x,y), график которой хотите построить. После этого необходимо сформировать матрицу значений функции в виде: Ai,j=f(xi,yj). |

| Теперь после выполнения команды Insert -> Graph -> Surface Plot в появившейся графической области достаточно ввести имя матрицы (без индексов). Если вы хотите, чтобы узловые точки были расположены через равные промежутки, воспользуйтесь формулами, изображенными на рисунке. |
| Для построения графика линий уровня данной функции необходимо поступать также как это было описано выше, только вместо команды (Поверхности) следует выбрать команду Contour Plot (Контурный). Аналогично, при помощи команды 3D Bar Plot (3D Диаграммы) можно построить трехмерный столбчатый график данной функции, при помощи команды 3D Scatter Plot (3D Точечный) - трехмерный точечный график, а при помощи команды 3D Patch Plot (3D Лоскутный) - трехмерный график поверхности в виде несвязанных квадратных площадок - плоскостей уровня для каждой точки данных, параллельных плоскости X-Y | 
|

| 
|

| Построение графика поверхности, заданной параметрически. |
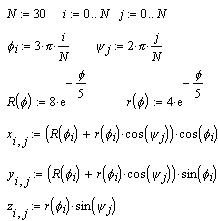
| Если поверхность задана параметрически, это означает, что все три координаты - x и y и z - заданы как функции от двух параметров u и v. Сначала необходимо задать векторы значений параметров ui и vj. Затем необходимо определить матрицы значений функций координат x(u,v), y(u,v) и y(u,v). |
| После выбора команды Surface Plot в MathCAD документе появится графическая область. В свободной ячейке внизу области надо указать В СКОБКАХ имена (без аргументов и индексов) трех матриц - x,y,z. | 
|

| Форматирование трехмерных графиков. |
Если вас не устраивает внешний вид созданного трехмерного графика, вы можете изменитьего, выполнив команду Format -> Graph -> 3D Plot или выполнив двойной щелчок мышкой на графической области. В результате на экране появится диалоговое окно 3-D Plot Format, позволяющее изменять параметры отображения графика. Мы рассмотрим здесь основные опции. Разобраться во всех тонкостях управлением видом графика вы можете самостоятельно, построив график и поэкспериментировав, выбирая те или иные опции.
Диалоговое окно 3-D Plot Format содержит несколько вкладок. Некоторые из них мы рассмотрим более подробно, а для других - опишем лишь их функциональное назначение.
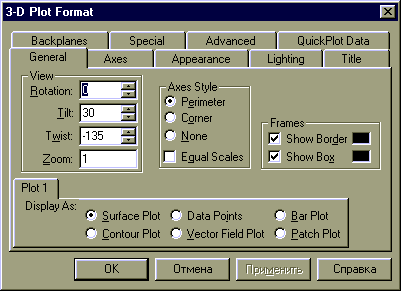
На вкладкеGeneral (Общие свойства) вы можете
- в области View задать направление взгляда наблюдателя на трехмерный график. Значение в поле Rotation определяет угол поворота вокруг оси Z в плоскости X-Y. Значение в поле Tilt задает угол наклона линии взгляда к плоскости X-Y. Поле Zoom позволяет увеличить (уменьшить) графическое изображение в число раз, равное цифре, указанной в поле.
|
|
- в области Frames опция Show box (Каркас) предназначена для отображения вокруг графика куба с прозрачными гранями, а опция Show border (Границы) позволяет заключить график в прямоугольную рамку.
- в области Plot 1 (Plot 2...) Display as (График/ несколько графиков Отобразить как) - имеются селекторные кнопки для представления графика в друих видах (контурный, точечный, векторное поле и др.)
Элементы вкладки Axes (Ось) позволяют изменять внешний вид осей координат.

|
|
При этом рядом с осями Ox и Oy указываются не значения узловых точек xi, yj, а значения индексов i и j, в то время как ось Oz размечается в соответствии с промежутком, которому принадлежат элементы матрицы значений Ai,j.
- Если установлена опция Auto Grid (Автосетка), программа самостоятельно задает расстояние между соседними отметками на осях. Вы можете сами указать число линий сетки, если отключите указанную опцию.
- Если установленна опция Auto Scale (Авошкала) , то MathCAD сам определяет границы построкния графика и масштабы по осям. Можно отключить данную опцию и для каждой оси самостоятельно задать пределы изменения переменных в полях Minimum Value(Минимум) и Maximum Value (Максимум).
Вкладка Appearance(Внешний вид) позволяет изменять для каждого графика вид и цвет заливки поверхности (область Fill Options); вид, цвет и толщину дополнительных линий на графике (область Line Options); наносить на график точки данных (опция Draw Points области Point Options), менять их вид, размер и цвет.
Вкладка Lighting (Освещение) при включении опции Enable Lighting (Наличие подсветки) позволяет выбрать цветовую схему для освещения, "установить" несколько источников света, выбрав для них цвет освещения и определив его направление.
Вкладка Backplanes (Задние плоскости) позволяет изменить внешний вид плоскостей, ограничивающих область построения: цвет, нанесение сетки, определение ее цвета и толщины, прорисовка границ плоскостей.
На вкладке Special (Специальная) можно изменять параметры построения, специфичные для различных типов графиков.
Вкладка Advansed позволяет установить параметры печати и изменить цветовую схему для окрашивания поверхности нрафика, а также указать направление смены окраски (вдоль оси Ox, Oy или Oz). Включение опции Enable Fog (Наличие Тумана) делает график нечетким, слегка размытым (полупрозрачным). При включении опции Perspective (Перспектива) появляется возможность указать в соответствующем поле расстояние до наблюдателя.
Вкладка Quick Plot Dataобсуждалась ранее в начале раздела.

| Кривая в пространстве. |
Трехмерные точечные графики можно использовать для построения изображения пространственных кривых. Пространственные кривые задаются, как правило, в виде (x(t),y(t),z(t)), где t представляет собой непрерывный действительный параметр.

| Поскольку при построении техмерной точечной диаграммы MathCAD позволяет отображать на графике только отдельные точки и соединяющие их линии, необходимо сначаоа определить три вектора координат - xi, yi, zi. |
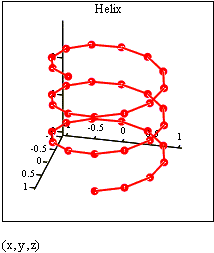
| Пространственная кривая создается командойInsert3D -> Graph ->Scatter Plot. Можно использовать наборную панель Graph, выбрав соответствующую пиктограмму. Для соединения точек необходимо на вкладке Appearance окна форматирования графиков указать опцию Line. |

| Векторные и градиентные поля. |
Команда Insert -> Graph -> Vector Field Plot (Поле векторов) служит для представления двумерных векторных полей v=(vx, vy).

| При этом векторное поле необходимо вначале определить как вектор-функцию двух координат - x и y. Затем задаются векторы значений узловых точек x и y. При помощи этих векторов компоненты векторного поля vx(x,y) и vy(x,y) генерируются в виде матриц значений vxi, j и vyi, j. |
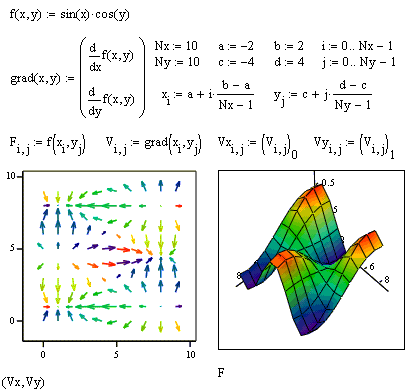
| Подобным образом можно построить градиентное поле скалярной функции f(x,y). Градиентное поле для функции двух переменных представляет собой двумерное векторное поле. Как и в остальных случаях, внешний вид изображения векторного поля можно легко изменить, выполнив двойной щелчок в области графика и изменив требуемые опции в открывшемся диалоговом окне 3-D Plot Format. |

| Поверхности, полученные вращением кривых вокруг осей. |
Интересные объемные фигуры можно получит, вращая некоторую кривую вокруг той или иной оси. Построение этих фигур вращения сродни параметрически заданным поверхностям.
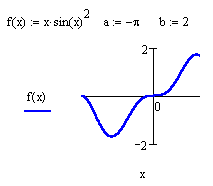
| При этом необходимо обеспечитьпересчет координат точек фигуры по известным из геметрии формулам. В MathCAD встроена функция CreateMesh, с помощью которой можно построить параметрически заданные поверхности. |
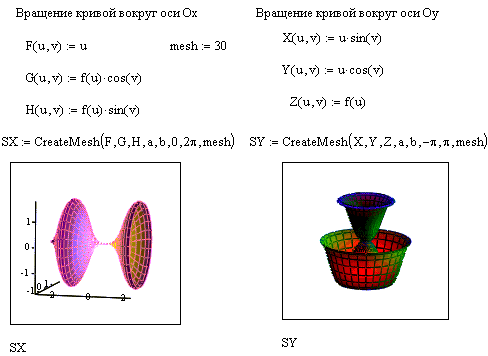
Дата добавления: 2014-12-24; просмотров: 3429;
