Середньої швидкості та за середньою швидкістю вихідної ланки

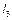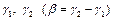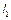Кривошипно - коромисловий механізм.Задано довжину коромисла , два його крайніх положення за допомогою кутів , а також коефіцієнт зміни середньої швидкості вихідної ланки 3. Потрібно знайти: довжини кривошипа , шатуна та стояка (рис.5.4, а).

Коефіцієнт зміни середньої швидкості - це відношення середніх кутових швидкостей вихідної ланки при марноході та робочому ході механізму

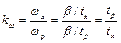. (5.7)

Рис. 5.4

Зазвичай величина коефіцієнта більша за одиницю, >1. Це пов’язано з тим, що при робочому ході механізму швидкість вихідної ланки обмежується технологічним процесом. При марноході такого обмеження немає, крім того, сили опору є значно меншими, і тому для підвищення продуктивності машини швидкість вихідної ланки вибирається більшою. Відповідно до цього, рух коромисла з положення 1 у положення 2 приймаємо за робочий хід – кривошип повернеться на кут , а рух у протилежному напрямі – за марнохід – кривошип повернеться на кут . Зазначимо, що більший з центральних кутів повороту кривошипа , що відповідає крайнім положенням вихідної ланки, називають кутом робочого ходу. Як слідує з рис. 5.4, а , за час робочого ходу та марноходу кривошип повернеться, відповідно, на кути , де 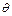- кут перекриття, кут між положеннями шатуна, що відповідають крайнім положенням коромисла.

Отже,

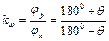. (5.8)

З виразу (5.8) знаходимо кут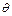

.

Після цього задача зводиться до знаходження центра обертання А кривошипа. Побудуємо кут ходу коромисла з вершиною у довільно вибраній точці D, а на його сторонах відкладемо довжину коромисла l . Отримуємо точки С₁, С₂. Проводимо бісектрису ЕD кута . На продовженні прямої ЕD зі сторони т.С₂ відкладаємо кут перекриття 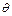. Через т.С₂, до перетину з продовженням ЕD, проводимо пряму, що паралельна стороні побудованого кута перекриття. З отриманої точки перетину F, як із центра, проводимо коло, що проходить через точки С₁, С₂. Коло радіусом r=C₂F буде геометричним місцем шуканих центрів обертання кривошипа, оскільки при виборі центра у будь-якій точці цього кола, кут перекриття дорівнюватиме заданому (кут, вписаний у коло, дорівнює половині відповідного центрального кута, 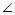С₁АС₂= С₁FC₂= 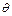). Щоб задача мала один розв’язок задамося додатковою умовою – центр обертання кривошипа знаходиться на осі абсцис (інколи додатковою умовою може бути обмеження ). Відмітимо, що для більшої точності радіус r=C₂F допоміжного кола можна порахувати за формулою

.

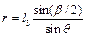Після цього довжини кривошипа та шатуна вираховуємо за формулами (5.5). Зазначимо, якщо в спроектованому механізмі максимальний кут тиску виявиться більшим за допустимий, слід вибрати інше положення центра обертання кривошипа (на колі радіуса r, вище за точку А ).

Кривошипно-повзунний механізм. У центральному кривошипно-повзунному механізмі швидкість повзуна в прямому та оберненому рухах однакова, коефіцієнт зміни середньої швидкості .

При синтезі таких механізмів часто виникає задача проектування за відомою середньою швидкістю вихідної ланки. Для центрального механізму хід повзуна дорівнює подвоєній довжині кривошипа. Тому можна записати

, (5.9)

де 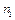, об/хв – частота обертання кривошипа.

З (5.9) одержуємо довжину кривошипа

.

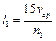Довжину шатуна визначаємо за вибраним коефіцієнтом .

Синтез кривошипно-повзунного механізму зі зміщенням за заданим коефіцієнтом зміни середньої швидкості та ходом вихідної ланки. Коефіцієнт зміни середньої швидкості вихідної ланки для даного механізму

. (5.10)

Розв’язавши рівняння (5.10) відносно кута 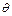, одержимо

.

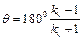Після цього задача зводиться до знаходження центра обертання А кривошипа, яка є аналогічною до розглянутої задачі для кривошипно-коромислового механізму. Проводимо через середину хода h повзуна пряму, перпендикулярну до С₂С₁ (рис. 5.4, б). Далі, через точку С₁ проводимо пряму, що складає кут 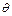з побудованим перпендикуляром. Коло радіуса r=C₁F , буде геометричним місцем шуканих центрів обертання кривошипа. Якщо задана величина зміщення е , то центр А знаходиться як точка перетину побудованої дуги кола r=C₁F та осі абсцис, що знаходиться на відстані е від ходу h.

Кулісний механізм. Розглянемо проектування цих механізмів на прикладі шестиланкового механізму з коливною кулісою (рис. 5.5). Для таких механізмів, як правило, відомо хід h вихідної ланки та коефіцієнт зміни її середньої швидкості .

Виявляється, що для механізмів даного виду коефіцієнт залежить лише від кутового ходу куліси .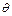

.

Як і у попередніх задачах, де зустрічається коефіцієнт зміни середньої швидкості вихідної ланки, знаходимо кут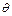

.

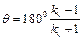Для визначення довжини куліси розглянемо її крайнє ліве положення

,

а з прямокутного 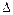АВС визначаємо співвідношення між розмірами ланок

(5.11)

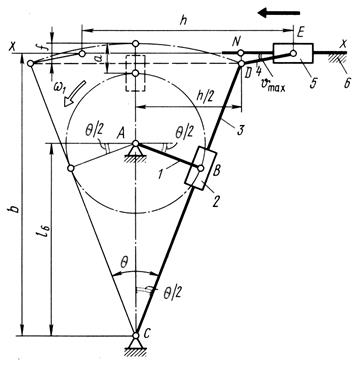
Рис. 5.5

З іншого боку при вертикальному положенні куліси можна записати таке співвідношення, що зв’язує розміри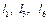

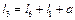, (5.12)

де а – розмір, що вибирають з конструктивних міркувань.

З виразу (5.12), після підстановки (5.11), знаходимо

.

Щодо кутів тиску, то при ведучому кривошипі кут =0, тобто за весь період руху напрям зусилля, що передається від кулісного каменя (повзун 2) до куліси 3, співпадає зі швидкістю точки прикладання зусилля. Даний факт є важливою позитивною властивістю цих механізмів.

З метою забезпечення найменшого кута тиску 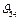при передачі зусилля від шатуна 4 до веденого повзуна 5 його напрямну хх необхідно розмістити таким чином, щоб вона ділила стрілку сегмента f навпіл, тоді

,

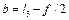де .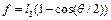

Довжина шатуна 4 виражається через заданий допустимий кут тиску з NDE

.

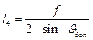Для інших кулісних механізмів синтез виконується подібним способом.