Кінематичний аналіз кулачкових механізмів

Кінематичне дослідження кулачкових механізмів полягає у визначенні закону руху вихідної ланки, тобто визначення залежності її переміщення, швидкості чи прискорення від часу або кута повороту кулачка, за відомими розмірами механізму, профілем кулачка і законом його руху. Розв’язок цієї задачі може бути виконаний графічним, графоаналітичним або аналітичним методами. Найчастіше застосовують графічний метод. Розглянемо побудову діаграми переміщення штовхача для кулачкового механізму, зображеного на рис. 6.2, а. Для цієї мети використовується метод обернення руху (інверсії), який дозволяє досить просто визначити відносне положення ланок механізму, без повторного викреслювання кулачка. Для цього всьому механізму в цілому умовно надається обертання з кутовою швидкістю кулачка, але в протилежному напрямі. Завдяки цьому кулачок зупиняється, а напрямна (стояк) разом зі штовхачем обертається з кутовою швидкістю (миттєві положення С₁, С₂, С₃,…). У такому випадку визначення переміщення штовхача значно спрощується. Для цього проведемо мінімальним радіусом основне коло. Відкладемо фазові кути. Поділимо кути віддалення 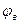та опускання 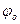на довільне число рівних частин. Точки поділу 1, 2, 3… нумерують відповідно до напрямку оберненого руху. За початкове положення прийнято положення, при якому вістря штовхача т. А займає крайнє нижнє положення А₀. Через точки 1, 2, 3…з центра О₁ кулачка проведемо промені до перетину з профілем кулачка в точках 1^/, 2^/, 3^/,… Продовження цих променів за профіль кулачка являють собою миттєві положення штовхача у його оберненому русі відносно кулачка. Переміщення вихідної ланки в кожному з положень являє собою відстань від до відповідної точки профілю кулачка (відрізки 11^/, 22^/, 33^/,…).

Для наочності та більшої зручності побудови діаграми переміщень інколи рекомендують з центра О₁ через точки 1^/, 2^/, 3^/…провести дуги до перетину їх з лінією А₀С руху штовхача. Одержимо точки А₀, А₁, А₂,…, що зображають відносні положення т. А вістря штовхача при обертанні кулачка, тобто переміщення штовхача.

Знайдені переміщення т. А вихідної ланки дають можливість побудувати графік її руху (рис. 6.2, б). Для цього відкладемо на осі абсцис прямокутної системи координат, у деякому масштабі 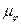, фазові кути 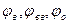(кут можна відкладати без масштабу). Далі ділянки осі абсцис, які відповідають кутам , поділимо на таке ж число частин, на яке поділені відповідні кути на кулачку. З точок поділу осі абсцис вздовж вертикалей в деякому масштабі 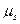відкладемо відповідні переміщення штовхача . З’єднавши плавною кривою кінці ординат, отримаємо діаграму переміщення штовхача залежно від кута повороту кулачка 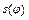. 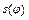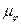Як відомо, при обертанні кулачка з постійною кутовою швидкістю, діаграма є одночасно діаграмою , якщо від масштабу перейти до .

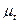Відмітимо, що з аналізу викладеного неважко зрозуміти порядок розв’язання основної задачі (оберненої) – синтезу кулачкового механізму, оскільки очевидно, що вона буде виконуватись у зворотному порядку.

За допомогою таких же нескладних побудов, за винятком незначних особливостей, можна визначити положення вихідної ланки та одержати закон руху для кулачкових механізмів інших типів. Наприклад, у випадку механізму з роликовим штовхачем потрібно спочатку побудувати центровий профіль кулачка, після цього задача розв’язується аналогічно до розглянутої.

Визначення швидкостей та прискорень.Цю задачу можна виконувати: методом кінематичних діаграм; методом планів; аналітичними методами; методом заміни кулачкового механізму важільним та наступним визначенням шуканих кінематичних параметрів для замінювального механізму. Якщо для кулачкового механізму визначені положення вихідної ланки та побудований графік 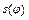або , то для визначення швидкостей та прискорень вихідної ланки зручніше за все застосувати метод кінематичних діаграм (рис. 6.2, б, в).

Необхідно зазначити, що графічне диференціювання може привести до значних неточностей, особливо у випадку двократного диференціювання при визначенні прискорень. Застосування методу планів дає можливість отримати точніші кінематичні характеристики механізму. Для цього рекомендують перейти до замінювального механізму, тобто, вищу кінематичну пару IV класу замінити умовною ланкою та двома парами V класу. Далі задача розв’язується як для звичайного важільного механізму. Зауважимо, що кожному окремому положенню кулачкового механізму буде відповідати замінюючий механізм зі своїми розмірами ланок. Побудова планів швидкостей та прискорень для кулачкового механізму може бути виконана і без заміни вищих кінематичних пар нижчими, тобто, безпосередньо по дійсній схемі кулачкового механізму.

При потребі отримання точніших результатів застосовують аналітичні методи дослідження кулачкових механізмів (як з допомогою замінювальних механізмів, так і без них).