Визначення основних розмірів кулачкового механізму
До основних розмірів кулачкового механізму відносяться: мінімальний радіус кулачка 
та зміщення 
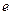для механізму зі штовхачем; мінімальний радіус кулачка та міжосьова відстань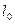 
для механізму з коромислом.
Кут тиску.Кут між нормаллю n-n у точці дотику взаємодіючих профілів вищої пари та вектором швидкості точки дотику вихідної ланки називається кутом тиску. При проектуванні механізмів з вищими парами цей кут має суттєве значення.
Розглянемо кулачковий механізм зі штовхачем (рис. 6.4). Якщо знехтувати силою тертя у вищій кінематичній парі , то можна вважати, що сила тиску, з якою кулачок 1 діє на штовхач 2, направлена по спільній нормалі n-n в точці дотику ланок. Гострий кут, що утворений напрямом сили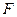 
тиску кулачка на штовхач і вектором швидкості штовхача називається кутом тиску 
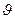. Зауважимо, що кут тиску є величиною змінною. Кут, що доповнює кут тиску до 900,називається кутом передачі (руху) ( 
).
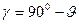Розкладемо силу 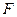за двома напрямками: по лінії руху штовхача 
та перпендикулярно до неї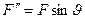 
. Сила 
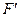- корисна сила, яка рухає штовхач; сила 
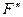- викликає перекошування штовхача в напрямній 3, внаслідок чого збільшуються реакції та сила тертя. Зрозуміло, що кулачковий механізм буде працювати тим краще, чим менший кут тиску. Не важко показати, що миттєвий коефіцієнт корисної дії кулачкового механізму зменшується зі зростанням кута тиску. При збільшенні кута тиску до деякого значення, що називається критичним 
, виникає явище заклинювання (самогальмування). Для нормальної роботи кулачкового механізму, кут тиску при будь-якому положенні кулачка має бути меншим за допустимий кут тиску, тобто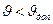 
.
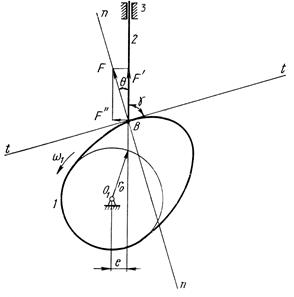
Рис. 6.4
Кут тиску можна виразити через геометричні параметри кулачкового механізму
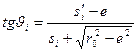, (6.1)
де 
– переміщення;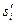 
‑ аналог швидкості штовхача, що відповідає куту 
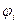повороту кулачка від початку фази віддалення; e ‑ зміщення напрямної штовхача відносно центра кулачка. Відмітимо, якщо при русі штовхача на фазі віддалення вгору вздовж напрямної, остання зміщена відносно центра кулачка праворуч, то при його обертанні проти стрілки годинника зміщення підставляється в (6.1) зі знаком плюс, при обертанні за годинниковою стрілкою - мінус. При зміщенні напрямної ліворуч від центра обертання кулачка знак 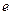змінюється на протилежний.
Подібною формулою виражається залежність між кутом тиску та основними параметрами коромислового кулачкового механізму.
Аналіз цих залежностей свідчить, що при вибраному законі руху та зміщенні 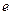можна зменшити кути тиску, збільшуючи мінімальний радіус кулачка, тобто габарити механізму. Аналогічно для коромислового кулачкового механізму, кути тиску зменшуються при збільшенні 
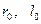, тобто розмірів механізму.
Отже, при проектуванні кулачкових механізмів основні розміри ‑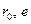 
або , 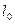визначаються з умови незаклинювання механізму. Виняток становить тарілчастий кулачковий механізм, для якого 
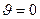(найпоширеніший випадок тарілки, перпендикулярної до напрямної) і r0 визначається з умови опуклості контуру .
Таким чином, одним із найважливіших питань при проектуванні кулачкових механізмів є вибір допустимого кута тиску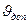 
, від величини якого залежить розподіл сил у механізмі, його К.К.Д., габаритні розміри і т. ін. Рекомендовані такі значення допустимого кута тиску: 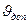=300…400 для механізмів зі штовхачем; 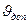=450…500 для коромислових механізмів. Якщо габарити механізмів дозволяють, то для зменшення втрат на тертя доцільно приймати менші значення кута тиску.
Визначення основних розмірів кулачкових механізмів за заданим допустимим кутом тиску. Аналітичний метод визначення основних розмірів кулачкових механізмів із штовхачем (з вістрям або роликом) полягає у розв’язку рівняння (6.1) відносно шуканих параметрів при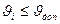 
. В основі графічного методу також лежить залежність (6.1).
Розглянемо задачу графічного визначення мінімального радіуса кулачка для механізму, зображеного на рис. 6.4.
Зауважимо, що у випадку механізму з роликовим штовхачем всі побудови є аналогічними, але в результаті буде знайдений не дійсного, а центрового профілю кулачка. Спочатку, на основі попередньо побудованих графіків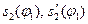 
, шляхом виключення параметра 
, будуємо графік 
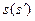, забезпечивши чисельно однакові масштаби по обох осях, 
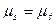(рис. 6.5). Для цього проводимо осі прямокутної системи координат. По осі ординат, в масштабі 
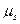, відкладемо від початку координат згідно графіка 
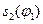переміщення штовхача (т. А0 відповідає нижньому початковому положенню штовхача, лежить на колі мінімального радіуса). Через отримані точки А0, А1, А2, …, проводимо прямі, паралельні осі абсцис та відкладаємо на них в масштабі 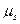, відрізки, що рівні 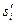. Причому для фази віддалення ці відрізки відкладаються в сторону обертання кулачка, а для фази опускання – в обернену. Сполучивши плавною кривою кінці відкладених відрізків, отримаємо криву 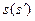. Після цього проводимо до кривої 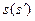дотичні прямі І-І та ІІ-ІІ під кутами 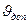до осі ординат. Центр обертання кулачка може знаходитись у будь – якій точці заштрихованої області (між дотичними), у цьому випадку завжди буде забезпечена умова 
. Відмітимо, що точка О перетину дотичних визначає мінімально можливе значення , тобто, найменші розміри кулачка та всього механізму, при якомусь певному 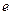. Якщо величина зміщення задана 
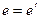, то проводять пряму y-y на відстані 
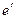від осі ординат (в масштабі 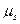). У цьому випадку мінімальний радіус дорівнює відрізку А0О2, в прийнятому масштабі. У випадку центрального кулачкового механізму (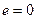 
) центр обертання кулачка буде знаходиться на продовженні лінії руху штовхача, в точці О1, а найменший радіус 
.
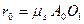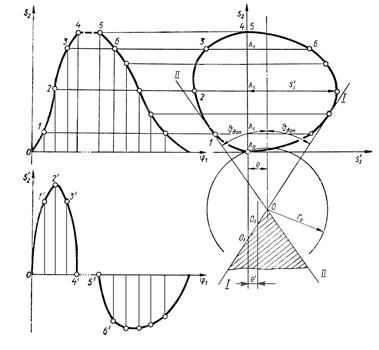
Рис. 6.5
Зауважимо, що при жорстких обмеженнях габаритних розмірів механізму беруть до уваги той факт, що небезпека заклинювання штовхача з силовим замиканням вищої пари має місце лише на фазі віддалення, оскільки при опусканні штовхач рухається під дією пружини (сили тяжіння). У цьому випадку при нереверсивному режимі роботи дотичну І-І проводять через т. А0. У кулачкових механізмах з геометричним замиканням вищої кінематичної пари умова повинна виконуватись як на фазі віддалення, так і опускання.
Така геометрична інтерпретація співвідношення (6.1) використовується і для графічного визначення габаритних розмірів кулачкових механізмів з коромислом.
Визначення мінімального радіуса кулачка за умовою опуклості профілю. Для кулачкових механізмів із плоским штовхачем при будь-якому положенні кулачка кут тиску сталий. Зокрема, якщо тарілка перпендикулярна до осі штовхача (найрозповсюдженіший випадок), кут тиску дорівнює нулю. Отже, при проектуванні таких механізмів кут тиску не може бути покладений в основу визначення . У даному випадку ставлять додаткову вимогу: профіль кулачка має бути опуклим. Лише при виконанні цієї умови кожна точка профілю зможе торкнутися тарілки штовхача. Профіль кулачка буде опуклим, якщо радіус кривини профілю в будь-якій точці буде більшим від нуля,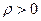 
. Цю умову можна виразити нерівністю
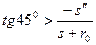. (6.2)
Нерівність (6.2) дозволяє графічно визначити величину , метод проф. Геронімуса. На основі попередньо побудованих графіків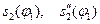 
будується графік 
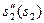. Для цього по осі ординат відкладемо значення 
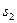, а паралельно осі абсцис - відповідні значення 
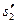(рис. 6.6). Вся побудова виконується в одному масштабі 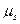. Сполучивши плавною кривою отримані точки, одержимо діаграму 
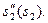До діаграми, на ділянці, що відповідає максимальному від’ємному значенню під кутом 450 до осі ординат проводиться дотична I-I. Згідно з нерівністю (6.2) за центр обертання кулачка може бути вибрана будь-яка точка, що розміщена нижче точки перетину дотичної з віссю ординат. Наприклад, на рис. 6.6 точка О1 , тоді мінімальний радіус А0О1, 
. Зауважимо, що в кулачкових механізмах з плоским штовхачем застосування ексцентриситету є недоцільним, оскільки призводить до збільшення габаритів механізмів.
Рис. 6.6
§ 6.5. Побудова профілю кулачка
Однією із основних задач синтезу кулачкових механізмів є побудова профілю кулачка. Розрізняють кінематичний та динамічний синтез кулачкових механізмів. При кінематичному синтезі значення мінімального радіуса кулачка задається, в той час як при динамічному значення – слід попередньо визначити, користуючись допустимим кутом тиску, або з умови опуклості профілю.
Розглянемо послідовність побудови профілю кулачка, якщо задані: схема кулачкового механізму; максимальний хід та закон руху вихідної ланки; фазові кути; напрям обертання кулачка; мінімальний радіус кулачка.
В основі графічного методу побудови профілю кулачка лежить метод обернення руху.
Центральний кулачковий механізм (рис. 6.2, а). Вважається, що згідно з заданим законом руху попередньо побудована діаграма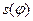 
переміщення штовхача (рис. 6.2, б).
Побудову профілю кулачка виконують у такій послідовності (обернено до порядку побудови діаграми переміщення штовхача при кінематичному аналізі механізму, § 6.2):
1. Із довільної точки О1 (вважаючи її центром обертання кулачка) проводимо коло радіусом , у масштабі 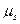(рис. 6.2, а). Зазначимо, що масштаб 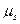зручніше прийняти рівним масштабу діаграми переміщення.
2. З точки О1 проводимо вертикальну пряму О1С, яку приймаємо за лінію руху штовхача. Точка перетину прямої О1С з колом визначить положення т. А вістря штовхача, що відповідає початку фази віддалення, т. А0.
3. Користуючись діаграмою переміщень, розмічаємо шлях т. А вістря штовхача 
в його абсолютному русі, точки А1, А2, А3, ..., А12. Для зручності побудови бажано, щоб вісь абсцис діаграми переміщень проходила через точку А0. Тоді ординати 1-1/, 2-2/, 3-3/,... діаграми переміщення безпосередньо визначають миттєві положення вістря штовхача.
4. Від прямої О1С в напрямі, протилежному напряму обертання кулачка, відкладемо фазові кути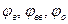 
. Ділимо кути 
на стільки ж рівних частин, на скільки вони поділені на діаграмі переміщення штовхача (6.2, б). Через точки поділу 1, 2, 3,…,13 на колі , з центру обертання кулачка проводимо промені, які в оберненому русі визначатимуть положення осі штовхача.
5. Переносимо за допомогою циркуля миттєві положення точки А—А1, А2, А3, …, А12 на відповідні промені, і отримуємо на них точки 1/, 2/, 3/,…13/- положення т. А вістря штовхача у відносному русі. Інколи для знаходження даних точок рекомендують безпосередньо з діаграми 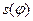відкласти від кола , на відповідні промені, переміщення штовхача 1-1/, 2-2/, 3-3/,…13-13/.
6. З’єднавши ці точки плавною кривою, одержимо частину профілю кулачка на кутах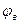 
та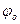 
. Профілі кулачка, що відповідають фазовим кутам 
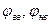, будуть окреслені дугами кіл, які описані з т.О1 відповідно радіусами О16/ та О113/. Таким чином, отримаємо дійсний профіль кулачка.
7. У випадку, якщо штовхач закінчується роликом, то отриманий профіль—центровий. Використовуючи центровий профіль, як геометричне місце центрів ролика у відносному русі, будуємо дійсний профіль. Дійсний профіль одержимо як обгинну сім’ю дуг радіуса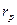 
проведених з точок центрового профілю (рис. 6.7, б).
Позацентровий кулачковий механізм з роликовим штовхачем. Вважаємо, що згідно з заданим законом руху попередньо накреслено графік функції 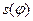(рис. 6.7, а).
Побудову профілю кулачка виконують у такій послідовності.
1. З довільної точки О1 проводимо у вибраному масштабі 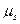кола радіусами і 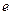(рис. 6.7, б).
2. Дотично до кола радіуса 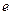проводимо лінію переміщення штовхача згідно з її положенням на схемі механізму. Точка перетину А0 цієї прямої з колом є положенням центра ролика, що відповідає початку фази віддалення (нижнє, початкове положення осі ролика).
3. Від т. А0 вздовж лінії у-у відкладаємо переміщення штовхача А1, А2, А3,…, згідно графіка переміщень 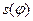. Точка А6 визначить положення центра ролика, що відповідає закінченню фази віддалення.
4. З’єднаємо т. А0 з центром обертання кулачка О1. Від прямої А0О1 в напрямі, протилежному напряму обертання кулачка, відкладемо фазові кути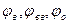 
. Ділимо кути на стільки ж рівних частин, на скільки вони поділені на діаграмі переміщення штовхача. Через точки поділу 1, 2, 3,…13, на колі проводимо дотичні до кола радіуса 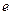, як ряд послідовних положень ліній переміщення штовхача у відносному русі навколо кулачка.
5. З центра О1 радіусами О1А1, О1А2, О1А3,… проведемо концентричні дуги до перетину з відповідними дотичними. Точки перетину 1/, 2/, 3/,… являють собою положення ролика у відносному русі. З’єднавши ці точки плавною кривою, одержимо центровий профіль кулачка.
6. Проводимо ряд дуг радіусом 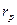з центрами, що розміщені на центровому профілі кулачка. Будуємо дійсний профіль кулачка як обгинну сім’ю цих дуг.
Вибір радіуса ролика. Для забезпечення руху вихідної ланки механізму за заданим законом необхідно, щоб радіус ролика був менший за радіус кривини в будь-якій точці центрового профілю кулачка
,
де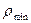 
– мінімальний радіус кривини центрового профілю кулачка.
Окрім того, радіус ролика обмежують умовою 
.
При проектуванні кулачкових механізмів радіус ролика приймають таким, щоб забезпечити виконання наведених умов. При цьому конкретне значення призначають у відповідності до стандартного ряду лінійних розмірів.
Кулачковий механізм з тарілчастим штовхачем (рис. 6.1, в).
Рис. 6.7
Побудова профілю даного механізму виконується аналогічно (включно по п.5) до описаної вище побудови профілю центрального кулачкового механізму з штовхачем. Різниця є лише в останньому етапі.
6. Через точки 1/, 2/, 3/,…, 13/ проводимо перпендикуляри до відповідних променів (рис. 6.6, б). Дані перпендикуляри являють собою послідовні положення площини тарілки штовхача у відносному русі навколо кулачка. Обгинна крива перпендикулярів і буде дійсним профілем кулачка.
ПИТАННЯ ДЛЯ САМОКОНТРОЛЮ
1. Переваги і недоліки кулачкових механізмів.
2. Як класифікують кулачкові механізми?
3. Назвіть фази руху кулачкових механізмів.
4. Назвіть методи кінематичного дослідження кулачкових механізмів.
5. Закони руху вихідної ланки.
6. Що називається кутом тиску і кутом передачі руху?
7. Яка різниця між кінематичним та динамічним синтезом кулачкових механізмів?
8. З яких умов визначається мінімальний радіус кулачка?
9. Послідовність побудови профілю кулачка.
Дата добавления: 2014-12-24; просмотров: 3364;