Необходимость и достаточность условий положительности коэффициентов для устойчивости корней

Как следует из (5.5), характеристическое уравнение замкнутой линейной системы не зависит от того, относительно какой переменной составляются дифференциальное уравнение системы и какие возмущающие и задающие воздействия в систему вводятся. Решение задач по исследованию устойчивости систем во всех случаях основано на использовании характеристических уравнений.

Необходимым условием устойчивости линейной системы любого порядка является положительностьвсех коэффициентов характеристического уравнения этой системы.

Пусть имеется характеристическое уравнение замкнутой системы (5.5). Это уравнение можно представить в виде произведения множителей, содержащих корни.

(5.6)

Если все корни характеристического уравнения будут отрицательными, то все множители в (5.6) будут положительными

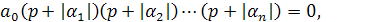(5.7)

где р₁= - 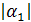, р₂= - 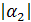, … , р_n=- 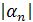– значения корней.

Производя перемножения в (5.7), получим уравнение (5.5), в котором все коэффициенты будут определяться положительными членами уравнения (5.7), т.е. будут положительными; нигде не могут получиться отрицательные числа и нули.

Аналогичное явление можно установить, если имеются комплексные корни с отрицательной вещественной частью

или

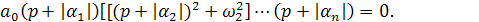(5.8)

Уравнение (5.8) также приводится к виду уравнения (5.5) с положительными коэффициентами. Для того чтобы получить отрицательные вещественные части корней, необходимо условие положительности всех коэффициентов уравнения.

Необходимое условие устойчивости для систем третьего и высших порядков обеспечивает отрицательность лишь вещественных частей корней, но не вещественных корней частей комплексных корней. Поэтому необходимого условия недостаточно для устойчивости систем выше второго порядка, так как по виду характеристического уравнения ещё неизвестно, какими являются корни. В этом случае требуется исследование устойчивости с помощью критериев устойчивости.

Пусть, например, имеется пара сопряжённых комплексных корней с положительной вещественной частью. Подставив в (5.6) значения корней, получим

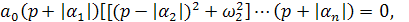(5.9)

или

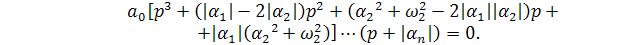(5.10)

Из (5.10) легко установить, что при некоторых соотношениях между числами α₁, α₂, ω₂ коэффициенты уравнения (5.10), приведённого к виду (5.5), будут положительны, в то время как часть корней имеет положительную вещественную часть и система неустойчива.