Описательная статистика

Одним из наиболее часто используемых средством в Пакете анализа является «Описательная статистика», которая позволяет быстро и просто вычислить основные статистические характеристики одномерных выборок и создает отчет, содержащий рассчитанные статистки по представленной выборке.

На рисунке 4.1 показан рабочий лист, содержащий три ряда данных (три независимые выборки, имеющие разные распределения), и диалоговое окно «Описательная статистика».

В диалоговом окне данного режима (рис. 4.1) задаются следующие параметры:

1. Входной интервал – указывается диапазон ячеек, в котором содержатся данные.

2. Группирование - демонстрируется, сгруппированы ли данные, и если сгруппированы, то по столбцам или строкам.

3. Метки в первой строке/Метки в первом столбце – устанавливается, если задается входной диапазон данных вместе с заголовками.

4. Выходной интервал/Новый рабочий лист/Новая рабочая книга – указывается, куда будут выводиться результаты расчетов.

5. Итоговая статистика — устанавливается в активное состояние, если в выходном диапазоне необходимо получить по одному полю для всех показателей описательной статистики.

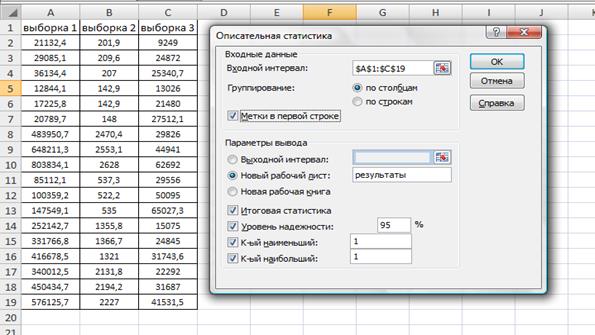
Рисунок 4.1. Три выборки и диалоговое окно «Описательная статистика»

Установка флажка Итоговая статистика указывает, что в итоговом отчете этого средства будут вычислены все статистические характеристики выборки, за исключением границы доверительного интервала для среднего и К-х наибольших и наименьших значений, для которых имеются отдельные опции: Уровень надежности, К-ый наименьший и К-ый наибольший. Если флажок Итоговая статистика не установлен, то выводится только то, что задается с помощью опций Уровень надежности, К-ый наименьший и К-ый наибольший.

Опция Уровень надежности указывает, надо ли вычислять границу доверительного интервала для среднего. В поле ввода рядом с этой опцией задается доверительный уровень в процентах.

В полях ввода рядом с опциями К-ый наибольший и К-ый наименьший указываются порядки выводимых наибольшего и наименьшего значений. Если эти порядки равны 1, то выводятся соответственно максимальное и минимальное выборочные значения.

Если имеются выборки разных размеров, то средство «Описательная статистика» правильно определяет размеры выборок, игнорируя пустые ячейки.

На рисунке 4.2 показан рабочий лист с результатами расчетов.

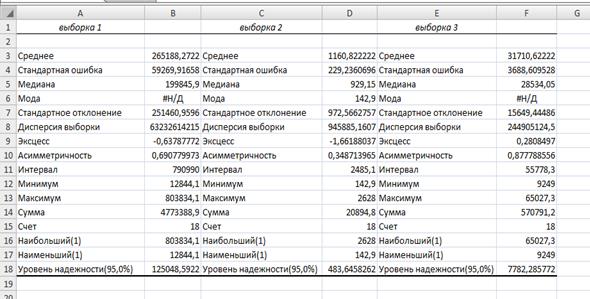
Рис.4.2. Результаты работы средства «Описательная статистика»

В таблице 4.2 приведены вычисляемые средством Описательная статистика статистические характеристики выборок, а также функции, которые возвращают те же самые характеристики.

Таблица 4.2

Выборочные характеристики, вычисляемые средством «Описательная статистика»

№	Числовая характеристика	Описание
	Среднее	Выборочное среднее; вычисляется по формуле 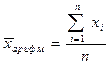. Функция СРЗНАЧ
	Стандартная ошибка	Оценка среднеквадратического отклонения выборочного среднего; вычисляется по формуле
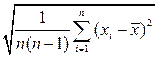
	Медиана	Значение медианы, т.е. квантиля порядка 0,5. Функция МЕДИАНА
	Мода	Значение моды. Вычисляется также, как и функцией МОДА. Если нет одинаковых выборочных значений, то возвращается значение ошибки #Н/ Д .

	Стандартное отклонение	Оценка среднеквадратического отклонения генеральной совокупности. Вычисляется по формуле "исправленного" среднеквадратического отклонения. 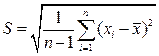Функция СТАНДОТКЛОН
	Дисперсия выборки	Оценка дисперсии генеральной совокупности. 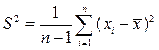Функция ДИСП
	Эксцесс	Выборочный коэффициент эксцесса. Функция ЭКСЦЕСС
	Асимметричность	Выборочный коэффициент асимметрии. Функция СКОС.
	Интервал	Размах выборки. Вычисляется как разность между максимальным и минимальным выборочными значениями
	Минимум	Минимальное выборочное значение. Функция МИН.
	Максимум	Максимальное выборочное значение. Функция МАКС
	Сумма	Сумма выборочных значений. Функция СУММ
	Счет	Объем выборки. Функция СЧЁТ
	Наибольший ( К)	К-е наибольшее значение. Если К = 1, то выводится максимальное выборочное значение. Функция НАИБОЛЬШИЙ
	Наименьший ( К)	К-е наименьшее значение. Если К = 1, то выводится минимальное выборочное значение. Функция НАИМЕНЬШИЙ
	Уровень надежности (g %)	Граница доверительного интервала для неизвестного математического ожидания с доверительным уровнем g %; доверительный интервал строится как выборочное среднее плюс-минус данное значение. Граница вычисляется с помощью распределения Стьюдента, т.е. здесь неявно используется предположение о нормальности распределения генеральной совокупности, Поэтому к данному показателю следует относиться осторожно, особенно при малых выборках.