Показатели вариации

В социально-экономическом анализе важно знать не только среднее (или серединное) значение признака, но и насколько равномерно распределены эти значения относительно среднего значения, а также знать количественную меру степени этой неравномерности.

В некоторых случаях отдельные значения признака близко примыкают к средней арифметической и мало от нее отличаются – значит средняя хорошо представляет всю совокупность. В других случаях, отдельные значения совокупности далеко отстают от средней, и средняя плохо представляет всю совокупность.

Изучая силу и характер вариации в выделенной совокупности можно оценить, насколько однородной является данная совокупность в количественном, а иногда и качественном отношении, следовательно, насколько характерной является исчисленная средняя величина.

Таким образом, измерение вариации, т.е. изменчивости признака у единиц совокупности, помогает познать сущность изучаемого явления.

Среди показателей, характеризующих вариацию признака, в экономическом анализе наибольшей популярностью пользуется дисперсия. Представляет собой средний квадрат отклонений значений признака от их средней величины.

По несгруппированным данным дисперсия считается по формуле:

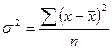. (4.6)

По сгруппированным данным формула дисперсии имеет вид:

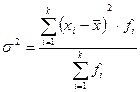. (4.7)

Для ручного счета лучше пользоваться формулой дисперсии следующего вида:

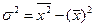. (4.8)

На практике желательно, чтобы показатель рассеяния выражался в тех же единицах измерения, что и значение признака. Дисперсия этим свойством не обладает, единицы измерения дисперсии соответствует квадрату единицы измерения рассматриваемого признака.

Извлекая квадратный корень из дисперсии, получаем показатель, имеющий ту же единицу измерения, что и анализируемый признак. Этот показатель называют среднее квадратическое (стандартное) отклонение, он представляет собой арифметическое значение корня квадратного из дисперсии:

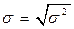. (4.9)

Стандартное отклонение измеряется в единицах измерения рассматриваемого признака и показывает на сколько в среднем отклоняются отдельные значения признака от своего среднего значения.

В научном анализе предпочтительно использование дисперсии, так как она имеет ряд полезных математических свойств, на практике же лучше работать со стандартным отклонением, поскольку эта мера легко интерпретируется.

Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеяния в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей).

Коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин, позволяет представить дисперсию как долю от средней величины.

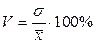. (4.10)

Чем меньше значение коэффициента вариации, тем однороднее совокупность по изучаемому признаку и типичнее средняя.[12] В статистике совокупности, имеющие коэффициент вариации больше 30-35 %, принято считать неоднородными.