Средние показатели

Результатом первого этапа сводки и группировки единиц статистической совокупности является представление их в виде графиков, таблиц или вариационных рядов.

Следующий этап обработки статистических данных – расчет средних показателей, дающих обобщенную количественную характеристику изучаемого массового процесса, отражаемого вариационным рядом.

Средняя величина – обобщенная количественная характеристика значений признака, полученная в расчете на единицу совокупности.

Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.

Сущность средней в том и заключается, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам

Взаимодействие элементов совокупности приводит к ограничению вариации хотя бы части их свойств.

Именно в объективности этой тенденции и заключена причина широкого применения средних величин на практике и в теории.

Главное значение средних величин состоит в их обобщающей функции, то есть замене различных индивидуальных значений признака средней величиной, характеризующей всю совокупность явлений.

Если средняя величина обобщает качественно однородные значения признака, то она является типической характеристикой признака в данной совокупности.

Среди средних наиболее распространена средняя арифметическая (простая и взвешенная).

Простая средняя арифметическая считается по несгруппированным данным и имеет следующий вид:

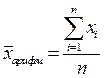, (4.1.)

где x_i – i-е значение осредняемого признака,

n – объем совокупности.

Взвешенная средняя арифметическая считается по сгруппированным данным и имеет следующий вид:

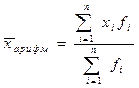, (4.2)

где f_i – частота i-го значения признака; показывает, сколько раз встречается i-e значение осредняемого признака.