Моделирование движения тела, брошенного под углом к горизонту.

Рассмотрим эту известную задачу с учетом сопротивления воздуха. Будучи брошенным под углом α к горизонту с начальной скоростью v₀, тело летит, если не учитывать сопротивления воздуха, по параболе, и через некоторое время падает на землю. Напомним элементарное решение этой задачи. Разложим скорость на горизонтальную и вертикальную составляющие:

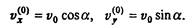
Поскольку движение по вертикали происходит под действием постоянной силы тяжести, то оно является равнозамедленным до достижения верхней точки на траектории и равноускоренным - после нее; движение же по горизонтали является равномерным. Из формул равноускоренного движения v_y = v 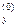-gt; раз в верхней точке v_y = 0, то время достижения верхней точки на траектории

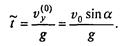
Высота этой точки

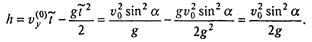
Полное время движения до падения на землю 2 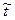; за это время, двигаясь равномерно вдоль оси х со скоростью v 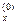, тело пройдет путь

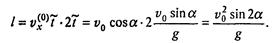
Для нахождения траектории достаточно из текущих значений x и у исключить t:

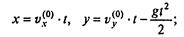
следовательно,

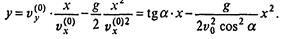(1)

Уравнение (1) - уравнение параболы.

Полученные формулы могут, в частности, послужить для тестирования будущей компьютерной программы. При достаточно большой начальной скорости сопротивление воздуха может значительно изменить характер движения. Прежде чем выписывать уравнения, оценим, какая из составляющих силы сопротивления - линейная или квадратичная по скорости - дает больший вклад в эту силу, и нельзя ли одной из этих составляющих пренебречь. Оценку проведем для шарика; по порядку величины оценка не зависит от формы тела. Итак, шарик радиусом r ≈ 0,1 м, движущийся со скоростью ~ 1 м/с, испытывает в воздухе линейную силу сопротивления F₁=k₁ v, где k₁ определяется свойствами среды и формой тела. Для шарика k₁= 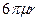. Это формула Стокса, где 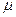- динамическая вязкость среды. Для воздуха при температуре 20 градусов Цельсия и давлении 1 атм. 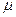=0,0182 Нс м^-2.

Итак,

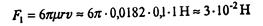
Квадратичная сила сопротивления F₂=k₂ v². Обычно представляют k₂= 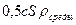, где с – коэффициент лобового сопротивления – безразмерен, и для шара с=0,4, S – площадь сечения тела, 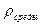-плотность среды (для воздуха 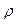=1,29 кг/м^-3). Отсюда

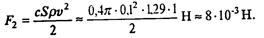
Величины F₁ и F₂ сопоставимые (как принято говорить, «одного порядка», так как они различаются менее, чем в 5 раз). При увеличении размера тела F₂ растет быстрее, чем F₁ (F₁ ~ r, F₂ ~ r²), при увеличении скорости F₂ также растет быстрее, чем F₁ (F₁ ~ v, F₂ ~ v²). Таким образом, если мы моделируем движение брошенного мяча, камня, то необходимо в уравнениях удерживать обе составляющие силы сопротивления, но если мы захотим моделировать полет снаряда, выпущенного из орудия, где скорость полета почти на всем его протяжении сотни метров в секунду, то линейной составляющей силы сопротивления можно пренебречь.

Проецируя уравнение 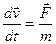на оси х и у, получаем

(*)

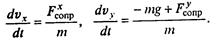Поскольку в каждой точке траектории сила сопротивления направлена по касательной к траектории в сторону, противоположную движению, то

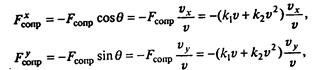
где θ - угол между текущим направлением скорости и осью х. Подставляя это в уравнение (*) и учитывая, что 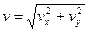, получаем уравнения движения в переменных v_x, v_y.

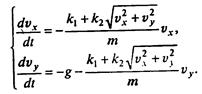(2)

Поскольку представляет несомненный интерес и траектория движения, дополним систему (2) еще двумя уравнениями

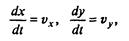(3)

и, решая их совместно с (2), будем получать разом четыре функции: v_x(t), v_y(t), x(t), y(t).

Прежде чем дать пример решения обсуждаемой задачи, покажем очень полезный прием, чрезвычайно популярный в физическом моделировании, называемый обезразмериванием. При решении конкретных задач мы пользуемся определенной системой единиц (СИ), в которой далеко не все числовые значения лежат в удобном диапазоне. Кроме того, абсолютные значения величин дают мало информации для качественного понимания. Скорость 15 м/с - много это или мало? Все дело в том, по сравнению с чем. Именно в сравнении с чем-то привычным и понятным мы обычно и воспринимаем слова «много» и «мало», даже если делаем это бессознательно. Идея обезразмеривания заключается в переходе от абсолютных значений расстояний, скоростей, времен и т.д. к относительным, причем отношения строятся к величинам, типичным для данной ситуации.

В рассматриваемой задаче это особенно хорошо просматривается. В самом деле, при отсутствии сопротивления воздуха мы имеем значения l, h, t, определенные выше; сопротивление воздуха изменит характер движения, и если мы введем в качестве переменных величины

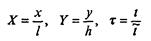
- безразмерные расстояния по осям и время, - то при отсутствии сопротивления воздуха эти переменные будут изменяться в диапазоне от 0 до 1, а в задаче с учетом сопротивления отличия их максимальных значений от единицы ясно характеризуют влияние этого сопротивления. Для скоростей естественно ввести безразмерные переменные, соотнося проекции скорости на оси x и у с начальной скоростью v₀:

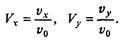
Покажем, как перейти к безразмерным переменным в одном из наших уравнений, например, во втором уравнении системы (2). Имеем:

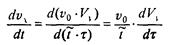
(так как постоянный множитель можно вынести за знак производной). Подставляя это в уравнение, получаем

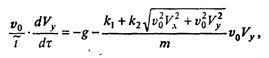
или

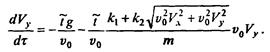
Подставляя

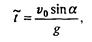
получаем

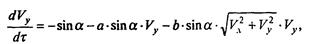
где безразмерные комбинации параметров, входящих в исходные уравнения,

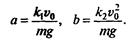
Выполним обезразмеривание во всех уравнениях (2), (3), получим

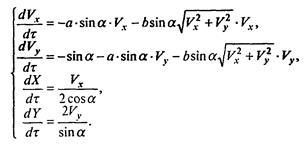(4)

Начальные условия для безразмерных переменных таковы:

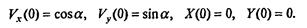
Важнейшая роль обезразмеривания - установление законов подобия. У изучаемого движения есть множество вариантов, определяемых наборами значений параметров, входящих в уравнения (2), (3) или являющихся для них начальными условиями: k₁, k₂, m, g, v₀, а. После обезразмеривания переменных появляются безразмерные комбинации параметров - в данном случае a, b, α - фактически определяющие характер движения. Если мы изучаем два разных движения с разными размерными параметрами, но такие, что а, b и α одинаковы, то движения будут качественно одинаковы. Число таких комбинаций обычно меньше числа размерных параметров (в данном случае вдвое), что также создает удобство при полном численном исследовании всевозможных ситуаций, связанных с этим процессом.

Наконец, как уже отмечалось, величины V_x, V_y, X, Y, τ физически легче интерпретировать, чем их размерные аналоги, так как они измеряются относительно величин, смысл которых очевиден. Прежде чем предпринимать численное моделирование, отметим, что при учете лишь линейной составляющей силы сопротивления модель допускает аналитическое решение. Но получаемая формула не из тех, которые привычно визуализируются, например, по сравнению с совершенно отчетливой формулой (1), и здесь компьютер может быть полезен в том, чтобы составить ясное представление о влиянии линейной части силы сопротивления на изучаемое движение.

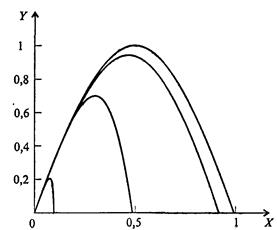
Рис. Семейство траекторий при α = 45°

и значениях α, равных 0,01; 0,1; 1 и 10 (кривые - справа налево)

На рис. приведены траектории четырех движений с разными значениями параметра α, характеризующего трение. Видно, как сильно оно влияет на движение - его форму, расстояния по вертикали и горизонтали.