Некоторые сведения о дифференциальных уравнениях
Дифференциальные уравнения – это уравнения, содержащие функцию и ее производную, т.е. уравнения вида 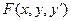 =0.
=0.
Пример:
1) y’=x
В дифференциальном уравнении неизвестным является функция.
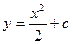
2) y’=y
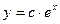
Из этих примеров можно заметить, что дифференциальные уравнения обычно имеют бесконечно много решений, зависящих от некоторой постоянной с. Обычно во всех приложениях требуется единственное решение из этого бесконечного множества. Чтобы выделить его, необходимо наложить дополнительные условия.
Задача Коши состоит в том, чтобы решить дифференциальное уравнение F(x,y,y’)=0 с дополнительным условием y(x0)=y0.
Теорема: Пусть функция F(x,y,y’) непрерывно дифференцируема по всем трем аргументам. Тогда задача Коши имеет решение, и это решение единственное.
Существует очень много различных приемов и методов для решения обыкновенных дифференциальных уравнений. Однако многие уравнения вообще не могут быть решены точно при помощи элементарных функций и интегралов от них (например, y’=x2+y2). Поэтому на практике используется приближенное решение таких уравнений. Существует много способов приближенного решения обыкновенных дифференциальных уравнений. Простейшим из этих способов является метод Эйлера.
Пусть нам нужно приближенно решить дифференциальное уравнение на отрезке [a,b]. Разобьем этот отрезок на много мелких отрезков. Далее вычислим приближенно значения функции, являющиеся решением уравнения, в точках x1, x2, ... , xn. Получим числа y1,y2, ... , yn. Построим ломаную, проходящую через точки (x1, y1), (x2, y2), ... , (xn, yn). Эта ломаная и будет приблизительным решением нашего уравнения.
Метод Эйлера служит для решения дифференциальных уравнений вида y’=f(x,y) при заданных x0, y0 . Мы разбиваем отрезок [a, b] на n равных отрезков. Длина каждого из отрезков 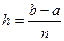 . Следовательно, x1=x0+h,
. Следовательно, x1=x0+h, 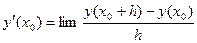
Если h достаточно мало, то мы можем записать приближенную формулу:
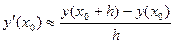 .
.
Тогда  .
.
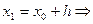
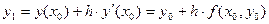 .
.
Аналогично вычислим
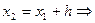
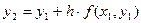 .
.
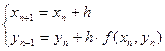 расчетные формулы метода Эйлера
расчетные формулы метода Эйлера
Система обыкновенных дифференциальных уравнений – это система вида
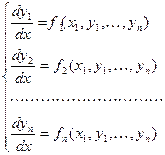 (1)
(1)
Неизвестными здесь являются функции y1, y2, ... , yn. Задача Коши состоит в том, чтобы найти решение системы (1) при начальных условиях
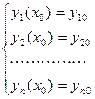 (2)
(2)
Т. е. в задаче Коши мы задаем значение всех функций в одной и той же точке x0.
Теорема. Пусть функции f1, f2, ... ,fn непрерывно дифференцируемы по всем аргументам. Тогда система уравнений (1) имеет решение, удовлетворяющее начальным условиям (2), и это решение единственное.
Для приближенного решения системы дифференциальных уравнений мы также будем использовать метод Эйлера. Нам нужно научиться вычислять значения функций y1, y2, ... , yn в точках xi.
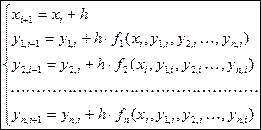
Вернемся теперь к задаче движения тела, брошенного под углом к горизонту. Там мы получили задачу Коши для системы из четырех уравнений. Теперь мы можем сделать вывод, что эта система имеет единственное решение. Запишем для этой системы расчетные формулы метода Эйлера.
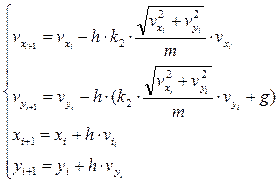
Дата добавления: 2014-12-20; просмотров: 2020;
