Тема 2. Этапы компьютерного математического моделирования.

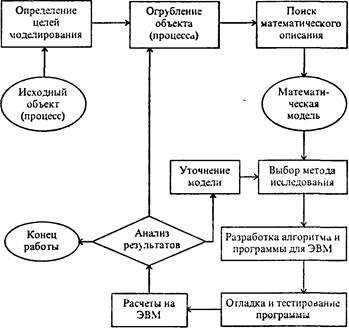
Рис. Общая схема процесса компьютерного математического моделирования

I. С чего начинается моделирование? На практике исходным пунктом часто является некоторая эмпирическая ситуация, выдвигающая перед исследователем «задачу», на которую следует найти «ответ». Однако, употребление таких слов, как задача и ответ, может ввести в заблуждение. Прежде всего, необходимо установить, в чем именно заключается задача. Это замечание связано с тем, что реальные ситуации редко бывают четко очерченными, а сложное взаимодействие с окружающей средой часто делает точное описание ситуации затруднительным. Процесс выделения «задачи», поддающейся математическому анализу, часто бывает продолжительным и требует владения многими навыками, не имеющими отношения к математике (например, беседы с коллегами-нематематиками, работающими в данной области; чтение всевозможной литературы, имеющей отношение к делу – важные элементы процесса моделирования).

II. Ситуации моделируют для разных целей.

Основные из них таковы:

1) модель нужна для того, чтобы понять, как устроен конкретный объект, какова его структура, основные свойства, законы развития и взаимодействия с окружающим миром (понимание);

2) модель нужна для того, чтобы научиться управлять объектом (или процессом) и определить наилучшие способы управления при заданных целях и критериях (управление);

3) модель нужна для того, чтобы прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект (прогнозирование).

Поясним это на примерах. Пусть объект исследования - взаимодействие потока жидкости или газа с телом, являющимся для этого потока препятствием. Опыт показывает, что сила сопротивления потоку со стороны тела растет с ростом скорости потока, но при некоторой достаточно высокой скорости эта сила скачком уменьшается с тем, чтобы с дальнейшим увеличением скорости снова возрасти. Что же произошло, обусловив уменьшение силы сопротивления? Математическое моделирование позволяет получить четкий ответ: в момент скачкообразного уменьшения сопротивления вихри, образующиеся в потоке жидкости или газа позади обтекаемого тела, начинают отрываться от него и уноситься потоком.

Пример совсем из другой области: мирно сосуществовавшие со стабильными численностями популяции двух видов особей, имеющих общую кормовую базу, «вдруг» начинают резко менять численность - и здесь математическое моделирование позволяет (с известной долей достоверности) установить причину (или, по крайней мере, опровергнуть определенную гипотезу).

Выработка концепции управления объектом - другая возможная цель моделирования. Какой режим полета самолета выбрать для того, чтобы полет был вполне безопасным и экономически наиболее выгодным? Как составить график выполнения сотен видов работ на строительстве большого объекта, чтобы оно закончилось в максимально короткий срок? Множество таких проблем систематически возникает перед экономистами, конструкторами, учеными.

Наконец, прогнозирование последствий тех или иных воздействий на объект может быть как относительно простым делом в несложных физических системах, так и чрезвычайно сложным - на грани выполнимости - в системах биолого-экономических, социальных. Если относительно легко ответить на вопрос об изменении режима распространения тепла в тонком стержне при изменениях в составляющем его сплаве, то несравненно труднее проследить (предсказать) экологические и климатические последствия строительства крупной ГЭС или социальные последствия изменений налогового законодательства. Возможно, и здесь методы математического моделирования будут оказывать в будущем более значительною помощь.

Главная цель моделирования – необходимость предсказывать новые результаты или новые свойства явления. Эти предсказания могут быть связаны с распространением уже существующих результатов или иметь более принципиальный характер. Часто они относятся к условиям, которые, по всей вероятности, будут иметь место в некоторый момент в будущем. С другой стороны, предсказания могут относиться к событиям, непосредственное экспериментальное исследование которых неосуществимо. Наиболее важный пример такого рода дают многочисленные прогнозы, которые делались на основе матем. моделей в программе космических исследований. Однако для этой цели моделируются не все ситуации: в некоторых случаях достаточно уметь описывать математическими средствами работу системы для того, чтобы добиться более широкого понимания явления. Обычно при таком матем. описании не учитывается элемент контроля, однако в моделях, построенных. Например, для исследования работы сетей (схемы движения поездов или самолетов) контроль часто является важным фактором. Действительно, многие модели в исследовании операций или технике имеют целью облегчить администрации процесс принятия решений.

Матем. модель представляет собой упрощение реальной ситуации. Ощутимое упрощение наступает тогда, когда несущественные особенности отбрасываются – и исходная сложная задача сводится к идеализированной задаче, поддающейся матем. анализу. Именно при таком подходе в классической прикладной математике возникли блоки без трения, невесомые нерастяжимые нити, невязкие жидкости и многие другие понятия подобного рода. Эти понятия не существуют в реальной действительности, они являются абстракциями, составной частью идеализации, предпринятой автором модели. И тем не менее их часто можно с успехом считать хорошим приближением к реальной ситуации.

Описанный образ действий при построении матем. моделей не является единственным, и этому совсем не стоит удивляться. В другом возможном подходе 1-ым шагом является построение простой модели нескольких наиболее характерных особенностей явления. Это часто делается для того, чтобы «почувствовать» данную задачу, причем делается еще до того, как сама задача окончательно сформулирована. Затем эта простая модель обобщается, чтобы охватить другие факторы, пока не будет найдено «приемлемое» или «адекватное» решение. Есть еще подход, при котором с самого начала вводится в рассмотрение большое число факторов. Он часто применяется в исследовании операций, и такие модели обычно изучают с использованием ЭВМ.

Важнейшее решение, которое часто принимается в самом начале процесса моделирования, касается природы рассматриваемых математических переменных. По существу они делятся на два класса. В один из них входят известные характеристики, т.е. величины, поддающиеся (по крайней мере теоретически) точному измерению и управлению. Они называются детерминированными переменными. В другой класс входят неизвестные характеристики, т.е. величины, которые никогда не могут быть точно измерены и имеют случайный характер. Они называются стохастическими переменными. Модель, содержащая стохастические переменные, должна по определению описываться аппаратом теории вероятностей и статистики. Детерминированные переменные часто, но отнюдь не всегда, требуют привлечения обычного матем. анализа.

Природа некоторых ситуаций бывает ясна не сразу, другие ситуации характеризуются переменными обоих видов. Для построения модели чрезвычайно важно правильное установление природы переменных.

III.Часто (но не всегда) параллельно со стадией постановки задачи идет процесс огрубления,выявления основных или существенных особенностей явления. В частности, для физических явлений этот процесс схематизации или идеализации играет решающую роль, поскольку в реальном явлении участвует множество процессов, и оно чрезвычайно сложно. Некоторые черты явления представляются важными. Другие – несущественными.

Возьмем, к примеру, движение маятника, образованного тяжелым грузом, подвешенным на конце нити. В этой «ситуации» существенным является регулярный характер колебаний маятника, а несущественным обстоятельством – то, что нить белая, а груз черный.

IV.Следующий этап - поиск математического описания. На этом этапе необходимо перейти от абстрактной формулировки модели к формулировке, имеющей конкретное математическое наполнение. В этот момент модель предстает перед нами в виде уравнения, системы уравнений, системы неравенств, дифференциального уравнения или системы таких уравнений и т.д.

V.После того, как существенные факторы выявлены, следующий шаг состоит в переводе этих факторов на язык математических понятий и величин и постулировании соотношений между этими величинами. Как правило, это самая трудная стадия процесса моделирования, причем здесь невозможно дать никаких общих рекомендаций.

После построения модели ее следует подвергнуть проверке. В действительности, адекватность модели до некоторой степени проверяется обычно в ходе постановки задачи. Уравнения или другие математические соотношения, сформулированные в модели, постоянно сопоставляются с исходной ситуацией. Существует несколько аспектов проверки адекватности. Во-первых, сама математическая основа модели (которая и составляет ее существо) д.б. непротиворечивой и подчиняться всем обычным законам математической логики. Во-вторых, справедливость модели зависит от ее способности адекватно описывать исходную ситуацию. Однако, вопрос о том, успешно ли проходит предложенная модель такую проверку, в значительной степени субъективен. Модель можно заставить отображать действительность, однако она не есть сама действительность. Наш маятник вполне реален, но его часто называют математическим маятником, и вот здесь нас поджидает ловушка! Дело в том, что объект, известный физикам и математикам под названием простого маятника, это всего лишь математическая идеализация реального объекта, и ничего больше. Это становится очевидным, когда мы замечаем, как размах колебаний нашего маятника уменьшается и, в конце концов, маятник останавливается. Модель математического маятника не предсказывает такого поведения. Означает ли это, что указанная модель неверна? Не обязательно. Ведь до полного затухания может пройти больше часа, а нас, возможно, интересуют лишь события, происходящие в первые 5 мин после начала движения.

Адекватность модели проявляется и в других формах. Например, описывая функционирование системы записи на прием в амбулатории, Шахани (1974) применил стандартный подход, основанный на теории очередей, что позволило ему прийти к некоторым заключениям относительно времени ожидания как пациентов, так и врача. (Теория очередей – раздел теории массового обслуживания. Изучает системы обслуживания, в которых требования, застающие систему занятой, не теряются, а ожидают ее освобождения и затем обслуживаются в том или ином порядке.) Его выводы не были основаны на принятии его модели в качестве истинной, т.е. правильно отражающей работу системы на всех этапах (такую модель на самом деле было бы трудно обосновать). Они просто основывались на решении вопроса о ее адекватности. Иначе говоря, достаточно ли хорошо для целей рассматриваемой задачи результаты, полученные на основе этой модели, отражают положение дел. Т.о., «решение» (даже одной и той же задачи, но в другой раз) зависит от критериев, выдвинутых автором модели, в такой же степени, как и от установления физических, экономических или любых других характеристик исходной ситуации. Можно потратить много времени на такое улучшение решения для данной модели, которое не оправдано самой постановкой задачи. Это связано, в частности, со степенью точности опытных данных. Так, если имеющиеся исходные данные известны с погрешностью, скажем, 5%, то, разумеется, бессмысленно предполагать решения, обеспечивающие погрешность, не превышающую 1%. Поэтому нужно подчеркнуть, что ответ, который невозможно реализовать на практике (хотя он и получен с помощью тонкого матем. анализа), оказывается бесполезным для данной задачи. Кроме того, можно сказать, что приближенный ответ, который получается быстрее, может оказаться более эффективным, чем более точный ответ, на получение которого уходит больше времени. Это часто свидетельствует в пользу непосредственного численного приближенного решения, позволяющего избежать затрат времени на поиски более изящного аналитического решения.

VI.Когда математическая модель сформулирована, выбирается метод ее исследования. Как правило, для решения одной и той же задачи есть несколько конкретных методов, различающихся эффективностью, устойчивостью и т.д. От верного выбора метода часто зависит успех всего процесса.

VII. Разработка алгоритма и составление программы для ЭВМ - это творческий и трудно формализуемый процесс. В настоящее время при компьютерном математическом моделировании наиболее распространенными являются приемы процедурно-ориентированного (структурного) программирования. Из языков программирования многие профессионалы-физики, например, до сих пор предпочитают FORTRAN как в силу традиций, так и в силу непревзойденной эффективности компиляторов (для расчетных работ) и наличия написанных на нем огромных, тщательно отлаженных и оптимизированных библиотек стандартных программ математической ориентации. В ходу и такие языки, как PASCAL, BASIC, С - в зависимости от характера задачи и склонностей программиста.

VIII. Отладка и тестирование программы.После составления программы решаем с ее помощью простейшую тестовую задачу (желательно, с заранее известным ответом) с целью устранения грубых ошибок. Это - лишь начало процедуры тестирования, которую трудно описать формально исчерпывающим образом. По существу, тестирование может продолжаться долго и закончиться тогда, когда пользователь по своим профессиональным признакам сочтет программу верной. Программистский фольклор полон историй об ошибках на этом пути.

Затем следует собственно численный эксперимент, и выясняется, соответствует ли модель реальному объекту (процессу). Модель адекватна реальному процессу, если некоторые характеристики процесса, полученные на ЭВМ, совпадают с экспериментальными с заданной степенью точности. В случае несоответствия модели реальному процессу возвращаемся к одному из предыдущих этапов.

IX.И наконец, переходим к вопросу об интерпретациивытекающих из модели выводов. Когда после многочисленных выкладок и математических манипуляций получается формула или иной результат, предстоит обратный перевод с математического языка на язык, на котором первоначально формулировалась исходная задача.

На этом процесс математического моделирования можно считать законченным.