Метод минимакса
Этот метод предназначен для ситуации, когда отсутствуют предварительные статистические сведения о вероятности диагнозов D1 и D2. Рассматривается «наихудший случай», то есть наименее благоприятные значения P1 и P2, приводящие к наибольшему значению (максимуму) риска.
Величина риска зависит отk0 и P1 (вероятность второго диагноза P2 = 1 - P1), в частности

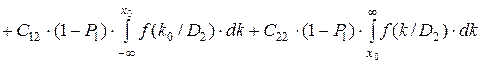 . (3.16)
. (3.16)
здесь C11 и C22 - стоимости правильных решений.
Для нахождения экстремума уравнение (3.16) преобразуют (приравнивают частные производные по k0 и P1 к нулю). Условие dR/dk0 = 0 дает
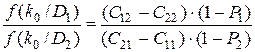 . (3.17)
. (3.17)
Условие dR/dP1 = 0 дает
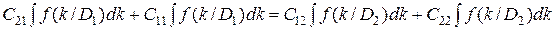 . (3.18)
. (3.18)
Значения k0 и P1, являющиеся корнями уравнений (3.17) и (3.18), определяют экстремальную точку R(k0, P1). Для одномодальных распределений величина риска становится минимальной (то есть минимальной среди максимальных значений, вызванных «неблагоприятной» величиной P1). По методу минимакса выбирают величину k0таким образом, чтобы при наименее благоприятных значениях P1 потери, связанные с ошибочным решением, были минимальными.
Опуская процедуры точного решения уравнений (3.17) и (3.18) (например, с помощью метода Ньютона) представим приближенные решения. Так, в первом приближении можно принять, что 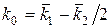 . Тогда из (3.17) находим наименее благоприятное значение вероятности исправного P*1 и неисправного P*2 состояний:
. Тогда из (3.17) находим наименее благоприятное значение вероятности исправного P*1 и неисправного P*2 состояний:
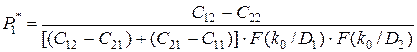 ,
,
 .
.
Величину риска определяем из равенства (3.16) при значениях k = k*0, P1 = P*1. Вероятность ложной тревоги и пропуска дефекта может быть найдена из соотношения
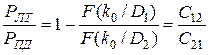 ,
,
где  - функция распределения D1 (в общем виде);
- функция распределения D1 (в общем виде);
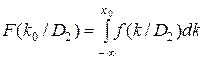 - функция распределения D2 (в общем виде).
- функция распределения D2 (в общем виде).
Дата добавления: 2014-12-20; просмотров: 2180;
