Теоретическая часть. Рассмотрим один из случаев плоского движения твердого тела, а именно: качение цилиндра по вогнутой цилиндрической поверхности.
 Рассмотрим один из случаев плоского движения твердого тела, а именно: качение цилиндра по вогнутой цилиндрической поверхности.
Рассмотрим один из случаев плоского движения твердого тела, а именно: качение цилиндра по вогнутой цилиндрической поверхности.
Плоским называется такое движение, при котором тело одновременно участвует в поступательном и вращательном движениях, например, качение цилиндра.
Пусть  – радиус цилиндрической поверхности,
– радиус цилиндрической поверхности,  – масса цилиндра,
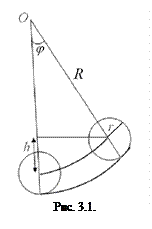
– масса цилиндра, 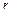 – его радиус (рис. 3.1). Если цилиндр вывести из состояния равновесия, то его ось будет совершать гармонические колебания по закону:
– его радиус (рис. 3.1). Если цилиндр вывести из состояния равновесия, то его ось будет совершать гармонические колебания по закону:
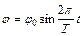 , (3.1)
, (3.1)
где 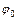 максимальное угловое отклонение оси цилиндра от вертикали,
максимальное угловое отклонение оси цилиндра от вертикали, 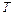 – период колебаний. Угловая скорость движения относительно оси цилиндрической поверхности находится с помощью дифференцирования выражения для угла отклонения
– период колебаний. Угловая скорость движения относительно оси цилиндрической поверхности находится с помощью дифференцирования выражения для угла отклонения  по времени:
по времени:
 , (3.2)
, (3.2)
где 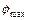 – амплитуда или максимальное значение угловой скорости этого движения. Катящийся без проскальзывания цилиндр вращается также относительно своей собственной геометрической оси. Максимальную угловую скорость этого движения можно представить в виде:
– амплитуда или максимальное значение угловой скорости этого движения. Катящийся без проскальзывания цилиндр вращается также относительно своей собственной геометрической оси. Максимальную угловую скорость этого движения можно представить в виде:
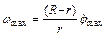 , (3.3)
, (3.3)
Будем рассматривать полную кинетическую энергию цилиндра как сумму кинетической энергии движения  относительно оси цилиндрической поверхности и кинетической энергии
относительно оси цилиндрической поверхности и кинетической энергии 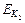 движения относительно собственной оси. При прохождении положения равновесия:
движения относительно собственной оси. При прохождении положения равновесия:
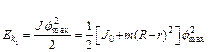 , (3.4)
, (3.4)
 , (3.5)
, (3.5)
где  –момент инерции цилиндра относительно оси цилиндрической поверхности,
–момент инерции цилиндра относительно оси цилиндрической поверхности, 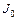 – момент инерции относительно собственной оси цилиндра. При написании соотношения (3.4) была использована теорема Штейнера, согласно которой:
– момент инерции относительно собственной оси цилиндра. При написании соотношения (3.4) была использована теорема Штейнера, согласно которой: 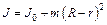 .
.
В процессе движения цилиндра периодически происходит превращение кинетической энергии в потенциальную и обратно. Максимальное значение потенциальной энергии будет равно (см. рис. 3.1):
 . (3.6)
. (3.6)
Будем полагать, что цилиндр совершает малые колебания около положения равновесия. Тогда 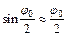 и, следовательно:
и, следовательно:
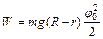 . (3.7)
. (3.7)
По закону сохранения механической энергии:
 . (3.8)
. (3.8)
Подставим полученные ранее выражения для кинетической энер-гии (3.4), (3.5) и потенциальной (3.7) в соотношение (3.8):
 . (3.9)
. (3.9)
Отсюда можно найти период колебаний:
 . (3.10)
. (3.10)
Кроме того, соотношение (3.9)можно использовать для определения момента инерции цилиндра 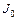 , измерив экспериментально период колебаний на данной вогнутой цилиндрической поверхности:
, измерив экспериментально период колебаний на данной вогнутой цилиндрической поверхности:
 . (3.11)
. (3.11)
Дата добавления: 2014-12-20; просмотров: 1120;
