Отказов и восстановлений технических систем

Машины, содержащие непоследовательно соединенные в смысле надежности элементы (т.е. наличие последовательного включения в смысле выполнения технологических операций), не обладают экспоненциальными распределениями. Поэтому включение их в систему в качестве ее элементов приводит к необходимости исследовать надежность системы при неэкспоненциальных распределениях.

При нагруженном резерве вероятность безотказной работы устройства подчиняется гиперэкспоненциальному распределению, а при ненагруженном или смешанном резервировании - обобщенному гамма-распределению. Это следует из простого свойства экспоненциальных распределений, а именно: свертка плотностей 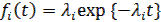есть плотность, подчиненная обобщенному гамма-распределению, причем, если все 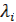различны, свертка указанных плотностей дает гиперэкспоненциальное распределение. Действительно, свертка всех плотностей f(t) с одинаковыми параметрами λ_i дает плотность гамма-распределений, а свертка гамма-распределений с разными параметрами, как известно, приводит к плотности обобщенного гамма-распределения. В частности, если все λ_i

С другой стороны, функционирование невосстанавливаемого устройства, элементы которого имеют экспоненциальные распределения, описывается графом состояний, в ветви которого проставлены параметры этих распределений. На рисунке 4.1 приведен фрагмент графа, содержащий одну из его вершин i₀, предшествующую вершину i₁., и все вершины i₁, i₂,..., i_k, следующие из данной вершины за один переход. Тогда для вероятности p_t (t) состояния i₀ справедливо равенство

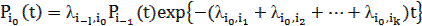(4.2)

Это значит, что вероятность пребывания системы в любом состоянии равна свертке экспоненциальных функций и представляет собой линейную комбинацию гамма-распределений. Отсюда следует, что вероятность безотказной работы также равна линейной комбинации гамма-распределений.

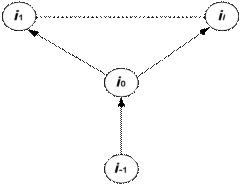
Рис. 4.1. Фрагмент графа, включающий вход и выходы,

связанные с состоянием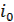

Линейная комбинация гамма-распределений превращается в линейную комбинацию экспоненциальных распределений, если все суммарные интенсивности переходов для любого пути графа различны. Поскольку для основного соединения и нагруженного резерва суммарная интенсивность при переходе на более низкий уровень графа убывает, то плотность распределения времени безотказной работы всей системы имеет гиперэкспоненциальное распределение. Для ненагруженного или скользящего резерва отмеченное свойство не имеет место, и поэтому плотность распределения времени безотказной работы системы имеет обобщенное гамма-распределение.

Подобные заключения можно сделать и для элемента с экспоненциально распределенным резервом времени, элементов, обладающих экспоненциальным распределением, но в которых учитываются такие дополнительные свойства, как возможность накопления нарушений, встроенный контроль, два вида отказов и др. В наибольшей степени это относится к механическим элементам, которые принципиально являются стареющими. Время безотказной работы механических элементов имеет распределение Вейбулла, или усеченное нормальное распределение [ ], то есть экспоненциальная модель не адекватна физическим процессам, протекающим в системе.

Для ремонтируемых систем время восстановления практически никогда не является экспоненциальным, так как складывается из времени обнаружения, локализации и устранения неисправности, то есть равно сумме (зависимых или независимых) обычно неэкспоненциальных распределений случайных величин. Причинами неэкспоненциальности распределений являются: 1) большое число механических устройств; 2) восстановление; 3) неодновременность работы элементов; 4) искусственная и естественная избыточность.

Таким образом, проблема анализа надежности восстанавливаемых систем с произвольными распределениями отказов и восстановления вытекает из свойств сложных систем.