КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ.
При изгибе в конструкции балки возникают следующие силовые факторы:
N, Q, Mизг. Поперечные силы вызывают в поперечных сечениях касательные напряжения.
Рассмотрим балку прямоугольного сечения, нагруженную внешними силами.
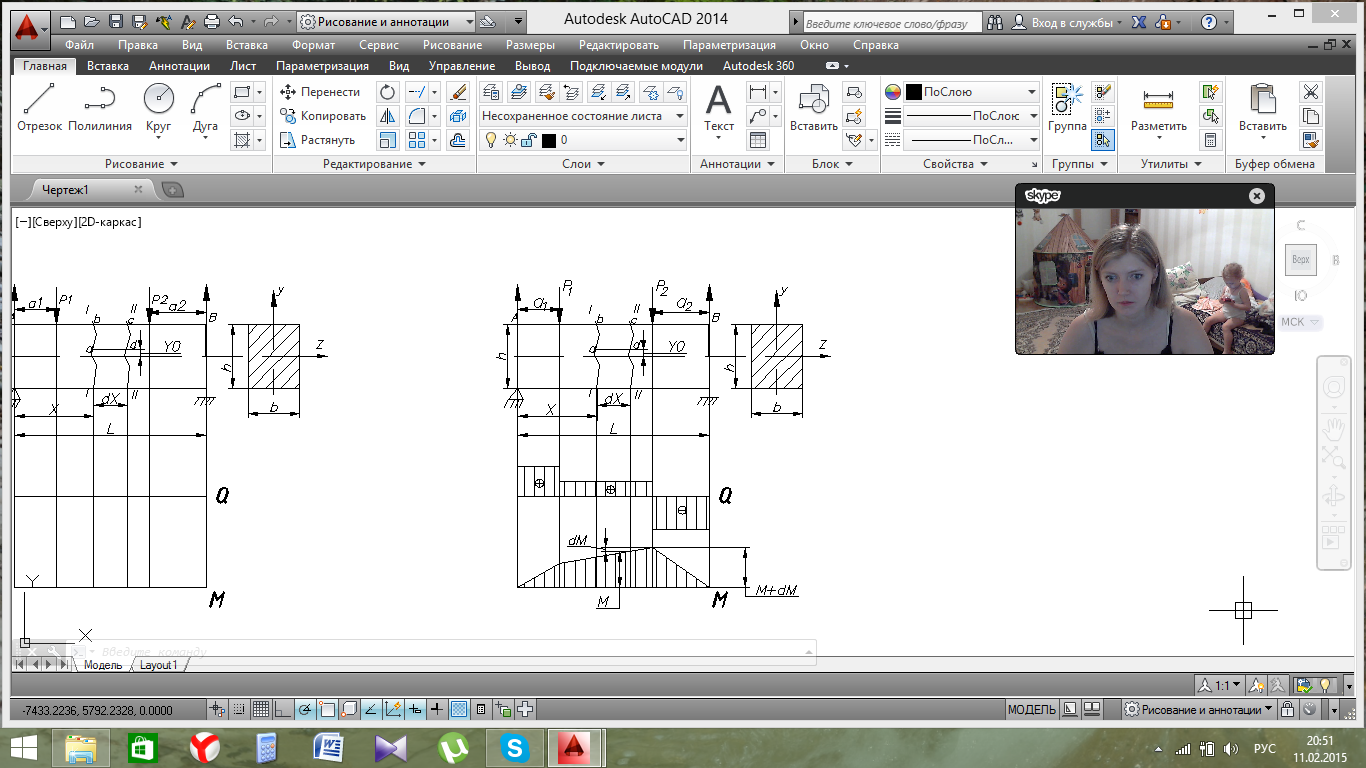
Рис.1.1. Расчетная схема балки.
Рассечем балку сечением 1-1, отстоящим от опоры А на расстоянии Х и сечением 2-2 на расстоянии Х+dX, а также плоскостью аd, параллельной плоскости ХОZ. При этом получим элемент abcd, который находится в состоянии равновесия за счет действия на него внутренних упругих сил.
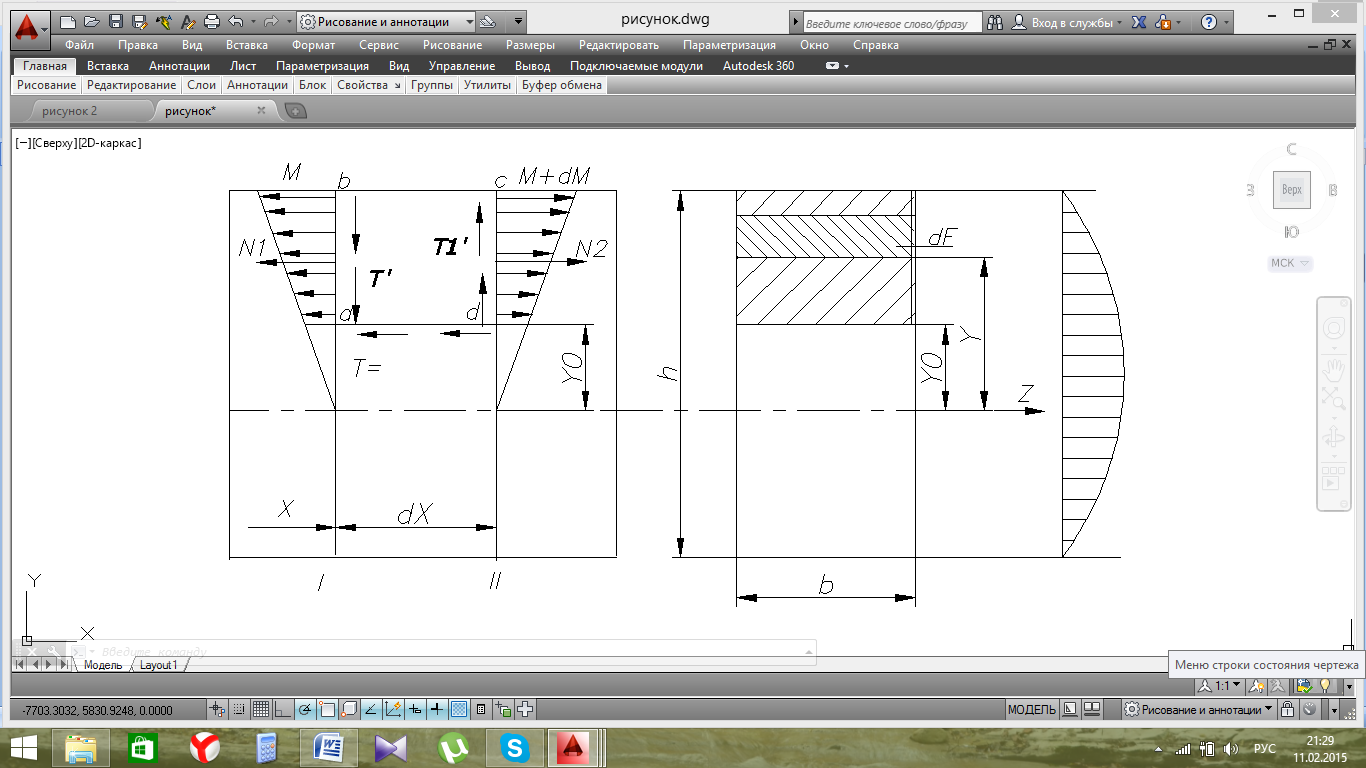
Рис.1.2. Эпюра касательных напряжений по высоте балки.
Согласно эпюрам Q и Мизг по левой грани ab действуют равнодействующие сдвигающих Т' и нормальных N1 сил. По правой грани cd действуют равнодействующие сдвигающих Т'1 и нормальных N2 сил.
Сдвигающие силы Т' = Т'1 , действующие по левой и правой граням будут равны между собой по закону парности касательных напряжений (Если в каком – нибудь сечении Т'1 касательное напряжение, то в сечении перпендикулярном будет действовать такое же по модулю напряжение, но обратного знака).
Условие равновесия элемента
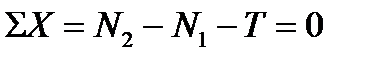
Выразим каждую силу через напряжение
Нормальные напряжения дают усилие N1
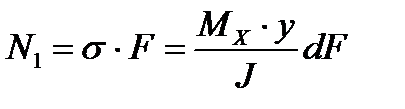
J – момент инерции сечения относительно нейтральной оси.
Нормальные напряжения дают усилие N2
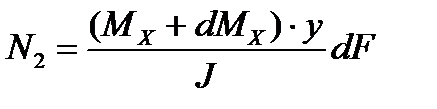
Величина сдвигаемой силы равна:
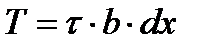
b·dx – площадь нижней грани рассматриваемого параллелепипеда.
Подставляя величины усилий, получим:
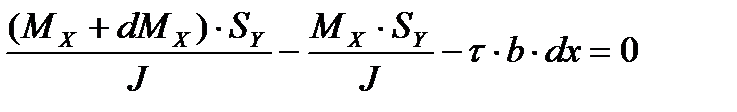
где 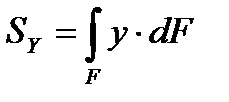
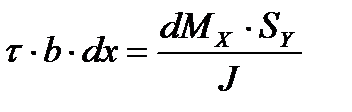 разделив на b∙dx и
разделив на b∙dx и 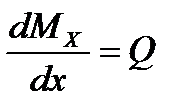
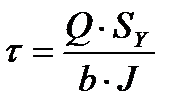
Выведенная формула впервые была получена Журавским и носит его имя.
Формулируется: Касательные напряжения в поперечных и продольных сечениях балки прямоугольного сечения прямо пропорциональны поперечной силе, действующей в сечении и статическому моменту и обратно пропорциональны осевому моменту инерции поперечного сечения балки и ширине сечения балки.
Установим закон распределения касательных напряжений по высоте сечения.
Касательные напряжения τ пропорциональны Sy.
Определим величину статического момента заштрихованной части сечения, т.е. площади АВСД.
Sх = F∙у
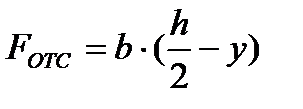 (отс - отсеченная часть)
(отс - отсеченная часть)
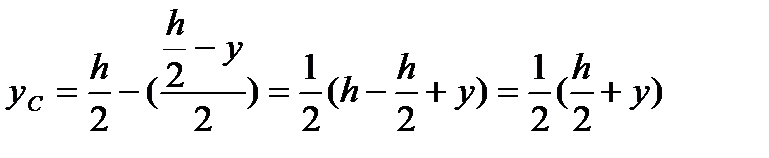
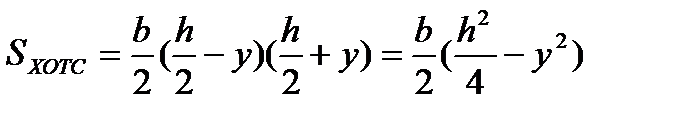
Статический момент находится в квадратичной зависимости от расстояния до нейтрального слоя. Касательное напряжение будет находится в той же зависимости, эпюра касательных напряжений по высоте балки будет очерчиваться кривой второго порядка.
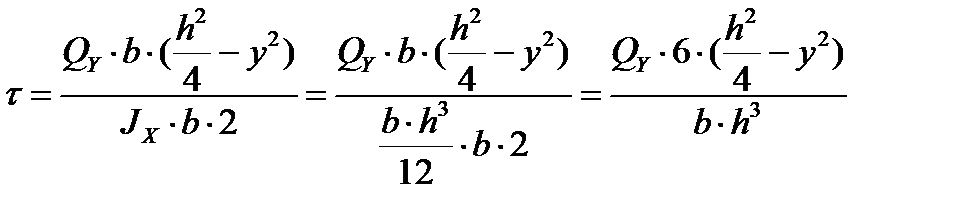
при у = h/2 τ=0
при у = 0 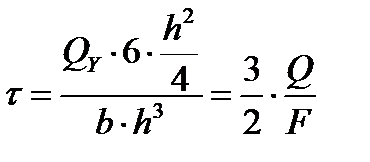
ПОЛНАЯ ПРОВЕРКА БАЛОК НА ПРОЧНОСТЬ.
Согласно эпюрам нормальных и касательных напряжений по высоте балки, нормальные напряжения имеют наибольшую величину в наиболее удаленных волокнах, а касательные напряжения достигают максимального значения по нейтральному слою. Следовательно, есть промежуточные волокна ,которые одновременно испытывают как нормальные, так и касательные напряжения
Рассмотрим балку, нагруженную системой внешних сил и построим эпюры Qу и Мх.

Рассечем балку. Согласно эпюрам Q и Мизг в любом поперечном сечении действуют поперечные силы и изгибающие моменты.
Возьмем по высоте поперечного сечения в точке приложения силы Р2 пять элементов и проанализируем их напряженное состояние.
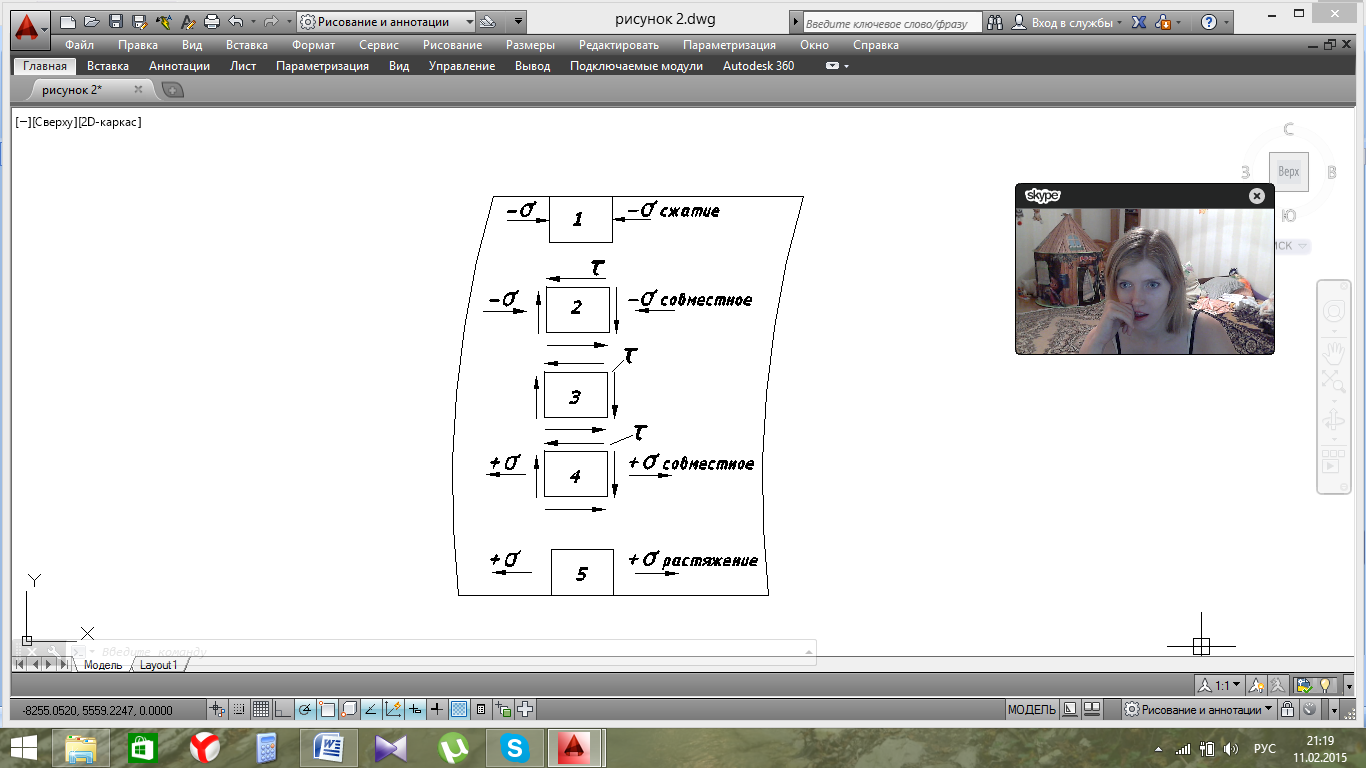
1. По граням элементов 1 и 5 действуют только нормальные напряжения : элемент 1 сжат, элемент 5: – растянут. Напряжения по граням этих элементов определяются по формулам
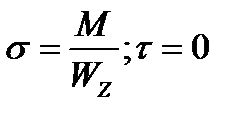 элементы 1 и 5 находятся в линейном напряженном состоянии.
элементы 1 и 5 находятся в линейном напряженном состоянии.
2. По граням элементов 2 и 4 действуют нормальные и касательные напряжения, т.е. элементы находятся в плоском напряженном состоянии. Напряжения по граням этих элементов определяются по формулам
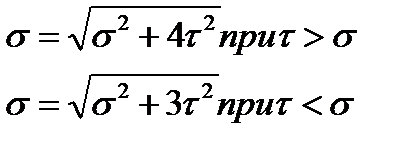
3. Элемент 3, лежащий на нейтральном слое балки, находится в состоянии чистого сдвига. Касательное напряжение определяется по формуле Журавского.
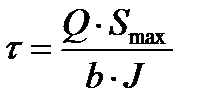
4. В опасном сечении могут находится точки 1 и 5 в сечении, где действует Ммах. Условие прочности запишем так: 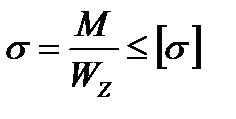
5. Опасно нагруженной может оказаться точка 3 в сечении, где действует Qмах. Условие прочности запишем так: 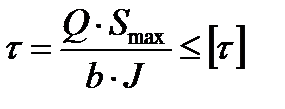
6. В точках 2 и 4 напряжения σ и τ в отдельности могут не представлять опасности. Однако поскольку они действуют одновременно может быть создано предельное напряженное состояние. Условие прочности выглядят следующим образом:
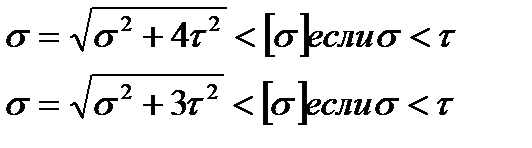
| <== предыдущая лекция | | | следующая лекция ==> |
| НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ. | | | ПОНЯТИЕ ЛИНЕЙНЫХ И УГЛОВЫХ ПЕРЕМЕЩЕНИЙ ПРИ ИЗГИБЕ. |
Дата добавления: 2017-03-29; просмотров: 1071;
