НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ.

При поперечном изгибе балок в их сечениях возникают нормальные и касательные напряжения. Для расчета балок важно знать распределение напряжений по высоте балки.

Рассмотрим участок балки. Линия m-n совпадает с нейтральным слоем балки, тогда волокна, лежащие выше линии m-n подвергаются растяжению, а нижележащие волокна – сжатию.

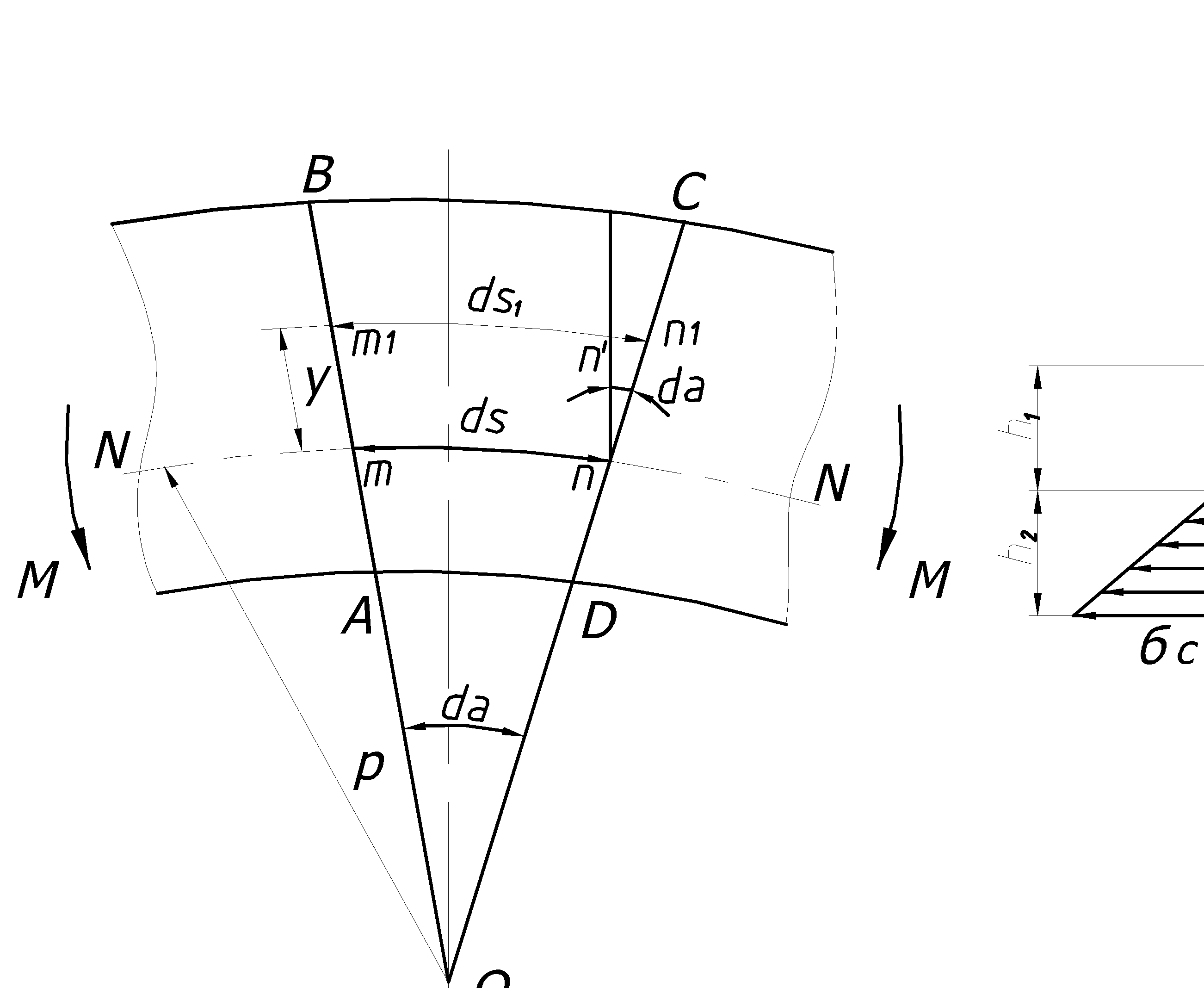
Рассечем балку сечениями ОВ и ОС, которые находятся на бесконечно близком расстоянии друг от друга. Расстояние между сечениями по нейтральному слою обозначим через dS, угол, ограничивающий эти сечения - через dα, а радиус кривизны - через ρ. Рассмотрим элемент АВСД, деформированный в результате действия на балку изгибающего момента М. Волокно на нейтральном слое только изогнулось, но напряжение в нем отсутствует, т.к. оно является границей между зонами растяжения и сжатия. Вышележащее волокно m1n1 длиной dS1, находящееся на расстоянии У от нейтрального слоя, подверглось растяжению на величину n'n1, представляющую собой абсолютное удлинение волокна m1n1.

Отношение nn1 к первоначальной длине волокна mn или к dS даст относительное удлинение волокна.

Из подобия треугольников nn’n1 и Omn:

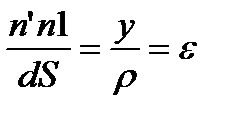
Относительная деформация пропорциональна растяжению волокна до нейтрального слоя.

Воспользуемся законом Гука для растяжения - сжатия

Учитывая, что Е и ρ величины постоянные, можно сделать вывод о том, что существует линейная зависимость между б и у.

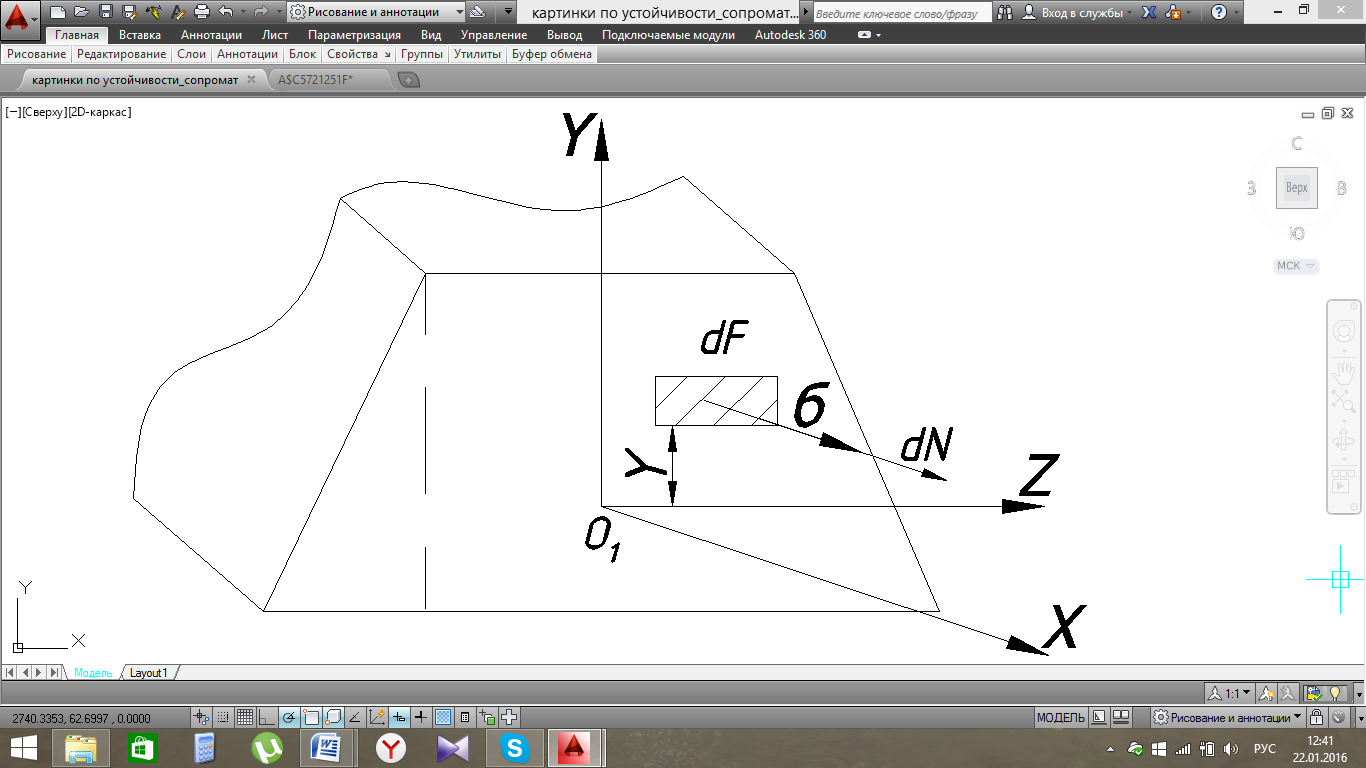
Воспользуемся дифференциальной зависимостью между нормальным напряжением σ и изгибающим моментом Мх.

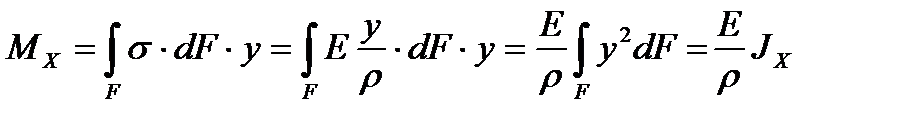
Отсюда

Формулу (3) подставим в формулу (2)

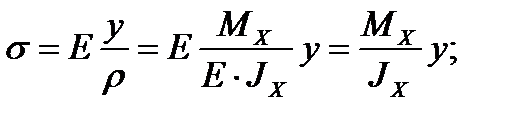
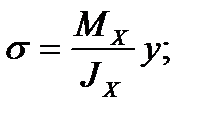
Чем дальше волокно находится от нейтральной линии , тем больше напряжение оно испытывает. эпюра нормальных напряжений - если у=0 , то σ = 0; - если у=уmax , то σ = σmax;

НАИБОЛЬШЕЕ НОРМАЛЬНОЕ НАПРЯЖЕНИЕ.

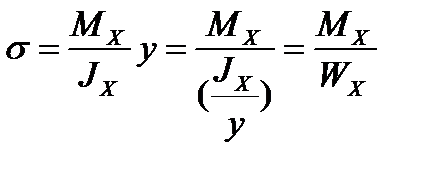
Где Wх – осевой момент сопротивления

Анализируя эпюру нормальных напряжений можно сказать, что наиболее нагруженными волокнами балки , подвергнутой поперечному изгибу являются волокна, наиболее удаленные от оси. Поэтому при проектировании конструкции нужно это учитывать и выбирать соответствующие профили.

Швеллер, Z , Двутавр.

РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ.

Для брусьев из пластичных материалов с сечением симметричным относительно нейтральной оси.

Условие прочности выглядит следующим образом

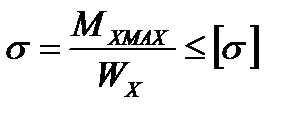
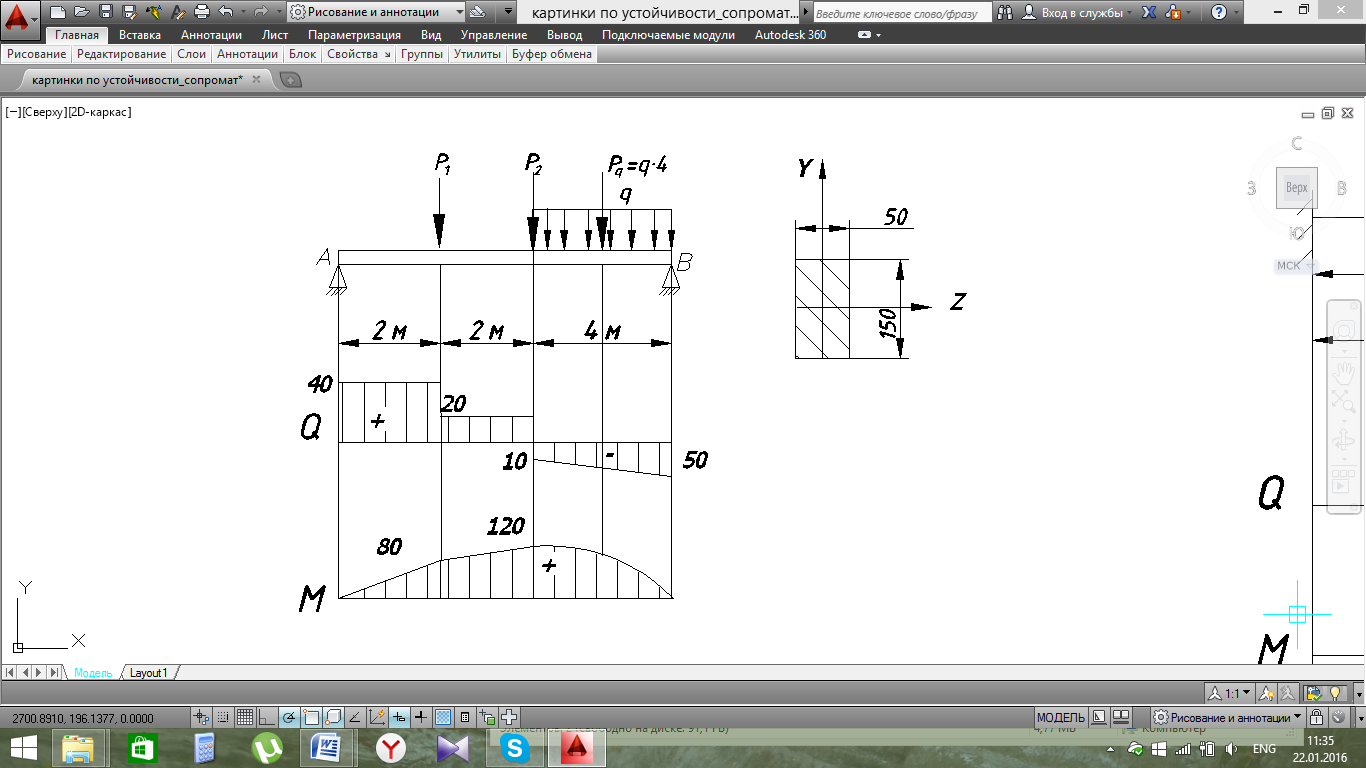
Задача. Для стальной балки прямоугольного сечения определить наибольшее нормальное напряжение

Дано: Р1=20кH; Р2=30кH; q=10кН/м; а=0,2м; [σ]=160н/мм2

Решение:

1.Определим опорные реакции балки А и В.

Составим уравнение моментов относительно т.т.А и В

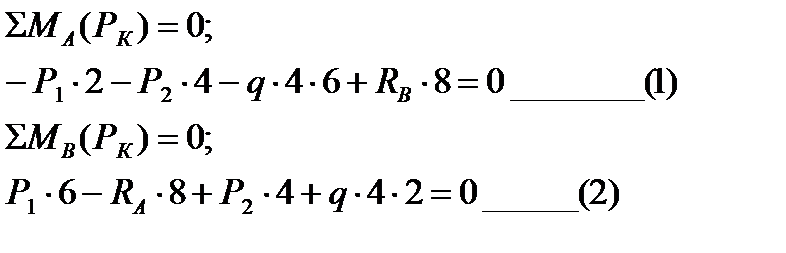
Из уравнения ( 1 )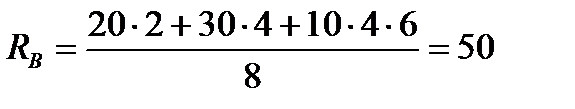

Из уравнения ( 2 ) 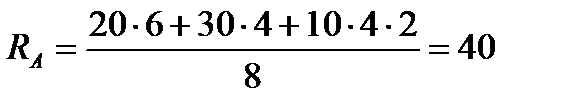кН

После определения опорных реакций разбиваем балку на участки.

1.Определим значения поперечных сил Qy в характерных точках А, В, С, Д и построим эпюру Qy. Поперечная сила на участке находится как алгебраическая сумма сил, лежащих слева от сечения.

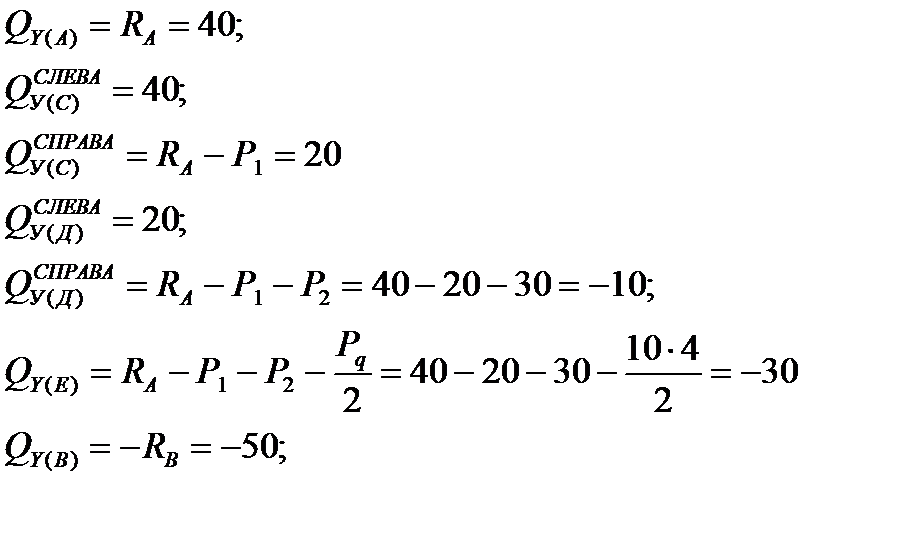
2. Определим значения изгибающих моментов Мх в характерных точках А, В, С, Д и построим эпюру Мх.

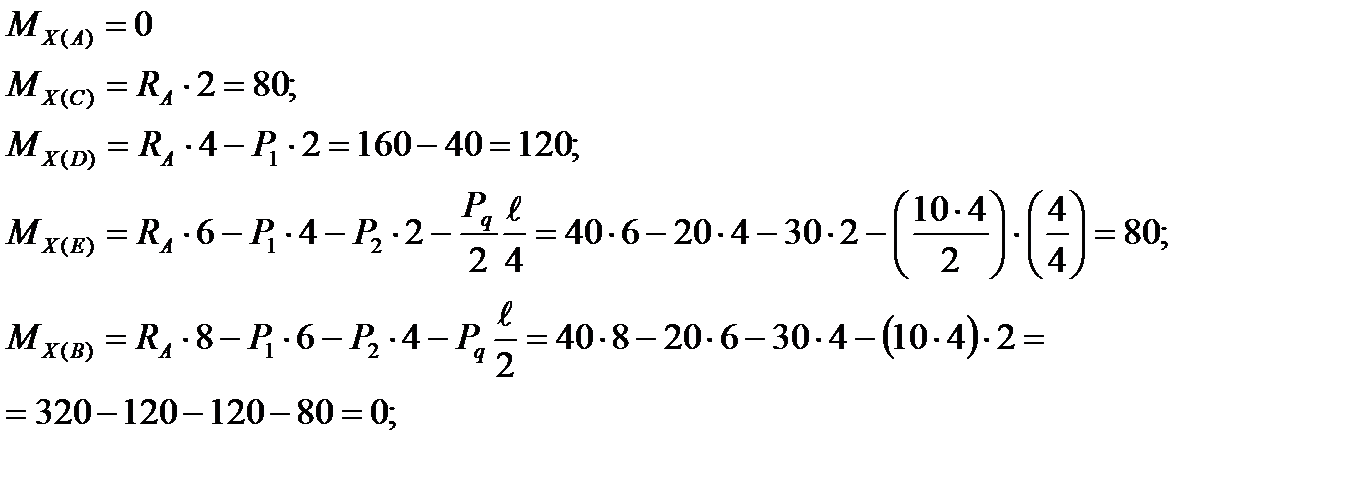
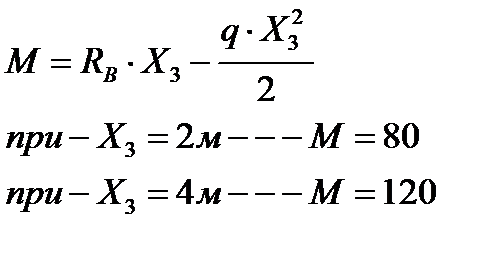М_XMAX=120кНм

Момент сопротивления: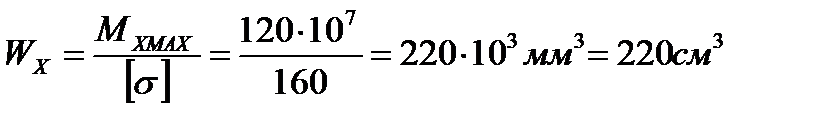

Подбираем сечение балки: из прямоугольника и уголка. Определим площади сечения балок. Сравнение масс балок осуществляется по сравнению площадей сечений.