Методические указания по теме
Процесс определения всевозможных индексов и факторного анализа сложного явления рассмотрим на примере двух фирм, выпускающих однородный продукт. Исходные данные приведены в табл. 24.
В табл. 24 итоговое количество продукта есть сумма его количества по фирмам, а итоговая цена представляет собой среднюю арифметическую взвешенную величину, найденную по формуле (11).
Таблица 24. Результаты работы двух фирм по выпуску однородного продукта
| Фирма | Базисный период (база) | Отчетный период (отчет) | ||
| Количество продукта q0, тыс.ед. | Отпускная цена p0, руб/ед. | Количество продукта q1, тыс.ед. | Отпускная цена p1, руб/ед. | |
| Итого | 21,20 | 20,23 |
Так, для базисного периода она равна
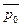 =
= 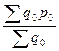 = (100*20+150*22)/(100+150) = 5300/250 = 21,20 руб./ед.
= (100*20+150*22)/(100+150) = 5300/250 = 21,20 руб./ед.
Для отчетного периода средняя цена равняется
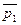 =
= 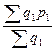 = (14*15+160*25)/(140+160) = 6100/300 = 20,23 руб./ед.
= (14*15+160*25)/(140+160) = 6100/300 = 20,23 руб./ед.
После этого в табл. 25 ведется расчет индивидуальных индексов.
Таблица 25. Определение выручки и индивидуальных индексов
| Выручка и индексы | База по фирмам | Отчет по фирмам | ||
| Выручка Q, тыс. руб. | 100*20=2000 | 150*22=3300 | 140*15=2I00 | 160*25=4000 |
Изменение выручки 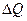 , тыс. руб. , тыс. руб.
| 2100-2000=100 | 4000-3300=700 | ||
| Доля фирм в количестве продукта d | 100/250=0,4 | 150/250=0,6 | 140/300=0,467 | 160/300=0,533 |
| Индивидуальные индексы: | ||||
| количества iq | 140/100=1,4 | 160/150=1,067 | ||
| отпускных цен ip | 15/20=0,75 | 25/22=1,136 | ||
| доли фирм id | 0,467/0,4=1,167 | 0,533/0,6=0,889 | ||
| выручки iQ | 2100/2000=1,05 | 4000/3300=1,212 |
Из табл. 25 заключаем, что общая выручка по периодам составляет:
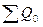 = 2000+3300 =5300 тыс. руб.;
= 2000+3300 =5300 тыс. руб.; 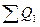 = 2100+4000 =6100 тыс. руб.
= 2100+4000 =6100 тыс. руб.
Ее абсолютное изменение равно 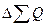 =6100-5300=800 тыс. руб., а общий индекс изменения равняется
=6100-5300=800 тыс. руб., а общий индекс изменения равняется 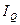 = 6100/5300 = 1,151.
= 6100/5300 = 1,151.
Контроль правильности расчетов по табл. 25 заключается в следующем.
1. Общее изменение выручки должно равняться сумме ее частных изменений: 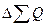 = 100+700 = 800 тыс. руб.
= 100+700 = 800 тыс. руб.
2. Произведение факторных индивидуальных индексов по периодам должно равняться соответствующему индивидуальному индексу выручки: iQ1=1,4*0,75 =1,05; iQ2= 1,067*1,136 = 1,212.
3. Сумма долей количества продукта по периодам должна равняться
единице: 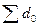 =0,4+0,6 = 1;
=0,4+0,6 = 1; 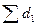 =0,467+0,533=1.
=0,467+0,533=1.
Затем переходим к расчету простых и агрегатных общих индексов. Простой общий индекс количества продукта - по формуле (111) 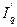 =(140+160)/(100+150)=300/250=1,2.
=(140+160)/(100+150)=300/250=1,2.
Агрегатный общий количественный индекс Ласпейреса - по формуле (114)
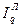 =
= 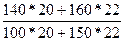 =6320/5300=1,192.
=6320/5300=1,192.
Агрегатный общий ценовый индекс Пааше - по формуле (116)
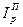 =
= 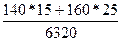 =6100/6320=0,965.
=6100/6320=0,965.
Контрольпо формуле IQ = 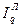
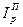 = 1,192*0,965 = 1,151.
= 1,192*0,965 = 1,151.
Агрегатный общий ценовый индекс Ласпейреса - по формуле (115)
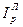 =
= 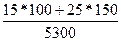 =5250/5300=0,9905.
=5250/5300=0,9905.
Агрегатный общий количественный индекс Пааше — по формуле (117) 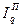 =6100/5250=1,162.
=6100/5250=1,162.
Контрольпо формуле IQ = 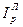
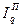 = 0,9905*1,162 =1,151.
= 0,9905*1,162 =1,151.
Средняя геометрическая величина из индексов Ласпейреса и Пааше (по методике Фишера) по формулам (119) и (120)
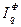 =
= 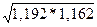 =1,1769
=1,1769 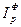 =
= 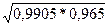 =0,9777
=0,9777
Общий индекс выручки как средний из ее индивидуальных индексов:
— с использованием только базисной выручки — по формуле (121)
IQ= 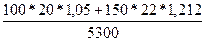 =1,151.
=1,151.
— с использованием только отчетной выручки — по формуле (122)
IQ= 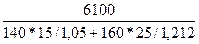 =1,151.
=1,151.
Индекс структурных сдвигов — по формуле
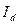 =
= 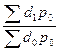 =
= 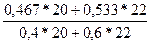 =21,07/21,2=0,994.
=21,07/21,2=0,994.
Контроль по формуле 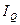 =
= 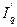
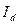
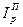 = 1,2*0,994*0,965 = 1,151.
= 1,2*0,994*0,965 = 1,151.
Индекс переменного состава — по формуле (137)
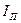 =
= 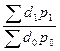 =
= 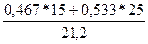 =20,33/21,2=0,959.
=20,33/21,2=0,959.
Контрольпо формуле 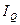 =
= 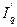
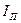 = 1,2*0,959=1,151.
= 1,2*0,959=1,151.
Далее выполняется факторный анализ общей выручки. Так ее изменение за счет изменения общего количества продукта определится по формуле (128) 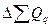 = (1,2-1)*5300 = 1060 тыс. руб.
= (1,2-1)*5300 = 1060 тыс. руб.
Изменение общей выручки за счет структурных сдвигов в количестве продукта находится по формуле (129) 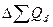 = 1,2*(0,994-1)*5300 = -40 тыс. руб.
= 1,2*(0,994-1)*5300 = -40 тыс. руб.
Изменение общей выручки за счет изменения отпускных цен - по формуле (130)
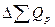 =1,2*0,994*(0,965-1)*5300 = -220 тыс. руб.
=1,2*0,994*(0,965-1)*5300 = -220 тыс. руб.
Контроль по формуле (131): 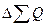 = 1060-40-220 = 800 тыс. руб.
= 1060-40-220 = 800 тыс. руб.
Результаты факторного анализа общей выручки заносятся в табл. 26.
Наконец, ведется факторный анализ изменения частной выручки по формулам (133) – (135). Так у первой фирмы изменение выручки за счет изменения общего количества продукта равно
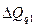 =(1,2-1)*2000 = 400 тыс. руб.
=(1,2-1)*2000 = 400 тыс. руб.
Аналогично у второй фирмы 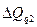 = (1,2-1)*3300 = 660 тыс. руб.
= (1,2-1)*3300 = 660 тыс. руб.
Контроль: 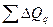 =400+660=1060 тыс.руб.
=400+660=1060 тыс.руб.
У первой фирмы изменение выручки за счет структурных сдвигов в количестве продукта равно
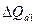 =1,2*(1,167-1)*2000 = 400 тыс. руб.
=1,2*(1,167-1)*2000 = 400 тыс. руб.
Аналогично у второй фирмы 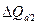 =1,2*(0,889-1)*3300 = -440 тыс. руб.
=1,2*(0,889-1)*3300 = -440 тыс. руб.
Контроль: 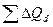 =400-440= -40 тыс.руб.
=400-440= -40 тыс.руб.
У первой фирмы изменение выручки за счет изменения отпускной цены равно
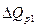 =1,2*1,167*(0,75-1)*2000 = -700 тыс. руб.
=1,2*1,167*(0,75-1)*2000 = -700 тыс. руб.
Аналогично у второй фирмы 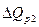 =1,2*0,889*(1,136-1)*3300 = 480 тыс. руб.
=1,2*0,889*(1,136-1)*3300 = 480 тыс. руб.
Контроль: 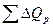 = -700+480= -220 тыс.руб.
= -700+480= -220 тыс.руб.
Результаты факторного анализа частной выручки также заносятся в табл. табл. 23, в которой все числа оказались взаимно согласованными.
Таблица 26. Результаты факторного анализа сложного явления
| Фирма | Изменение выручки, тыс.руб. | В том числе за счет изменения | ||
| количества продукта | структурных сдвигов | отпускных цен | ||
| -700 | ||||
| -440 | ||||
| Итого | -40 | -220 |
Таблица. 23 свидетельствует о правильности проведенного факторного анализа, поскольку в ней факторные изменения выручки, как по столбцам, так и по строкам в сумме равняются ее изменениям по отдельным факторам, фирмам и в целом.
[1] f – это начальная буква англ. слова frequency – частота
[2] В статистике, в отличие от математики, пределы суммирования не ставятся, а подразумеваются, так как абсолютные величины здесь не абстрактные, а смысловые (суммируются все величины совокупности – с первой по последнюю)
[3] Во многих учебниках по статистике встречается другое название индекса динамики – темп роста. Использование такого названия не совсем логично, так динамика может быть различна (не только рост, но и спад, а также стабильность), поэтому наиболее правильным является использование названия «индекс динамики» или «индекс изменения»
[4] Часто встречается и другое название темпа изменения – темп прироста, что не совсем логично (см. предыдущую сноску)
[5] Обычно (в т.ч. и в дальнейшем в данном пособии) в статистических формулах пределы суммирования не ставятся, а подразумеваются, т.е. подразумеваются именно такие пределы как формуле (11) – с 1-ой группы по N-ю (последнюю)
[6] Если приходится иметь дело с интервальным рядом распределения с неравными интервалами, то для сопоставимости нужно частоты или частости привести к единице интервала, полученное значение называется плотностью ρ, то есть ρ = f/h
[7] Единицы совокупности, имеющие значение признака, равное границе интервала, включаются в тот интервал, где это точное значение впервые указывается
[8] От греч. «гистос» – ткань, строение
[9] От греч. слов «поли» и «гонос» – многоугольник
[10] При четном числе единиц совокупности за медиану принимают полусумму из двух центральных вариант
[11] Получите формулы и произведите их расчет (по аналогии с формулами для расчета квартилей) самостоятельно
[12] Максимально возможные значения показателей вариации: Лmax = 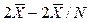 ;
; 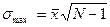 ;
; 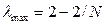 ;
; 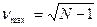
[13] При расчете параметров уравнения тренда на ЭВМ необходимость вести отсчет от середины ряда динамики отпадает. Например, для получения уравнения тренда в Microsoft Office Excel необходимо построить его график с помощью «Мастера диаграмм», после чего вызвать контекстное меню, нажав на правую кнопку мыши на построенном графике, и выбрать пункт «Добавить линию тренда», в появившемся окне выбрать подходящую математическую функцию и установить галочку «показывать уравнение на диаграмме»
[14] Используется при малом количестве уровней (n<30), в противном случае (n>30) вместо 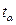 используют коэффициент доверия t нормального закона распределения (Приложение 1)
используют коэффициент доверия t нормального закона распределения (Приложение 1)
[15] Проявление стохастических связей подвержено действию закона больших чисел: лишь в достаточно большом числе единиц индивидуальные особенности сгладятся, случайности взаимопогасятся и зависимость, если она имеет существенную силу, проявится достаточно отчетливо
[16] Термин «стохастический» происходит от греч. «stochos» – мишень. Стреляя в мишень, даже хороший стрелок редко попадает в ее центр, выстрелы ложатся в некоторой близости от него. Другими словами стохастическая связь означает приблизительный характер значений признака
[17] Термин «корреляция» ввел в статистику английский биолог и статистик Ф. Гальтон в конце XIX в., под которым понималась «как бы связь», т.е. связь в форме, отличающейся от функциональной. Еще ранее этот термин применил француз Ж.Кювье в палеонтологии, где под законом корреляции частей животных он понимал возможность восстановить по найденным в раскопках частям облик всего животного
[18] Множественная корреляция изучается в курсе эконометрики на основе применения компьютерных программ (напр., специальная надстройка к Excel, SPSS и др.), в курсе статистики изучается только парная корреляция
[19] Данное условие означает отстутствие автокорреляции в коррелируемых рядах динамики, проверка на данное условие изучается на дневной форме обучения (при необходимости – см. конспект лекций для дневного отделения)
[20] Проделать это самостоятельно
[21] Термин «регрессия» ввел в статистику Ф. Гальтон, который изучив большое число семей, установил, что в группе семей высокорослыми отцами сыновья в среднем ниже ростом, чем их отцы, а в группе семей с низкорослыми отцами сыновья в среднем выше отцов, т.е. отклонение роста от среднего в следующем поколении уменьшается – регрессирует
[22] Параметры a0 и a1 можно получить не только методом подстановки как приводится далее, но и методом определителей 2-го порядка (проделать данное задание самостоятельно)
[23] Сумма эмпирических (2864,09) и выравненных по прямой линии (2864,115) значений должна совпадать, но в нашем случае этого не происходит из-за округлений расчетов до 3-х знаков после запятой
[24] В числителе – сумма последнего столбца, а в знаменателе – сумма предпоследнего столбца таблицы 22
Дата добавления: 2017-03-29; просмотров: 879;
