Как развивалось представление о числе. Десятичные дроби

Десятичные дроби. Первым руководителем созданной Улугбеком обсерватории был высокообразованный математик и астроном аль-Каши (ум. ок. 1430 г.).

Своими трудами аль-Каши внес большой вклад в математику. Им написаны книги «Ключ к искусству счета» и «Поучение об окружности». В книге «Поучение об окружности» ученый вычислил с большой точностью, во сколько раз окружность больше своего радиуса.

Аль-Каши был хорошо знаком с вавилонской шестидесятеричной системой счисления, распространенной и на шестидесятеричные дроби, т. е. на дроби со знаменателями 60: 60*60, 60*60*60 и т. д. Знакомство с этими дробями и с десятеричной позиционной системой Индии навело ученого на мысль применить десятеричную позиционную систему к дробям. Он первым начал разрабатывать этот раздел в науке. Аль-Каши стал записывать дроби в одну строку с числами в десятеричной системе. Чтобы отделять целое число от десятеричного, он пользовался вертикальной чертой или чернилами разного цвета; например, целое число записывал черными чернилами, а дробные знаки — красными.

В Европе о трудах аль-Каши долгое время не знали. Потребность же в более простых вычислениях с дробями с развитием науки и культуры росла, математики настойчиво искали пути решения этой проблемы. В 1585 г., независимо от аль-Каши, нидерландский ученый Симон Стевин (1548—1620) сделал важное открытие, о чем написал в своей книге «Десятая». Это маленькая работа (всего 7 страниц) содержала объяснение записи и правил действий с десятичными дробями. С. Стевин еще не пользовался запятой, но писал дробные знаки в одну строку с цифрами целого числа. При этом он нумеровал десятичные знаки, вписывая порядковые номера в окружности рядом с цифрой или над цифрой. Например, число 12,761 он записывал так:

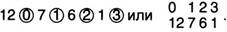
В первом примере вместо запятой стоит нуль в кружке, десятые доли обозначены знаком 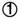, сотые — 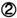и т. д. Во втором примере цифры в верхней строке указывают, сколько нулей содержит предшествующий десятичный знак (семь десятых, две сотых и шесть тысячных). Приведем один из примеров сложения десятичных дробей из руководства С. Стевина.

Десятичные дроби постепенно распространились в Европе, но лишь в XIX в. они стали пользоваться широкой известностью в связи с введением десятичной системы мер.

Применение запятой при записи дробей впервые встречается в 1592 г. Несколько позже — в 1617 г. отделять десятичные знаки от целого числа предложил Джон Непер (1550—1617) —знаменитый шотландский математик, изобретатель логарифмов. В России впервые о десятичных дробях было сказано в «Арифметике» Магницкого. 

Как развивалось представление о числе. На ранних ступенях развития человечества представление о числе у людей складывалось из счета различных предметов — плодов, деревьев, людей, животных, изделий и пр. В то время человек приобрел понятие натурального числа. Вначале он знакомился с небольшими числами. Расширение запаса чисел шло медленно. Довольно долго люди знали счет только до двух. Затем счет постепенно распространился до семи, и это число казалось очень большим, что подтверждается многими пословицами и поговорками, сохранившимися до наших дней: «Семеро (т. е. большое число людей) одного не ждут» или «Один с сошкой (с сохой) — семеро с ложкой» и др.

Затем люди овладели счетом в пределах трех-четырех десятков.

В то время у многих народов число 40 выглядело как предел счета, оно служило названием неопределенно большого числа. С тех пор, например, слово сороконожка мы понимаем как «много ножка». Выражение сорок сороков употребляли, чтобы сказать, что это число предметов невозможно назвать. Позже таким числом у славян стало тьма — десять тысяч, а потом тьма-тьмущая.

При счете множества предметов единица являлась наименьшим числом, при этом необходимости делить единицу на части не возникало. Но когда люди научились измерять различные величины — длину, массу, время и т. д,, то у них довольно часто при измерениях получались излишки (остатки), в которых единица меры не укладывалась. Чтобы точнее производить измерения, появилась необходимость делить, или ломать, единицу. Возникла потребность в дробях. Дроби были открыты значительно раньше того, как люди поняли, что натуральный ряд чисел бесконечен.

Дроби получались в результате не только измерений, но и деления. Используя только целые числа, во многих случаях деление нельзя было выполнить. Когда же люди познакомились с дробями, стало возможным разделить любое натуральное число на другое, кроме 0. Однако долгое время математики не считали дроби числами. Их принимали как особые знаки, и только. Дробь определяли как собрание нескольких равных частей или долей единицы. Знаменитый греческий математик Евклид (IV в. до н. э.), разъясняя, что надо понимать под числом, указывал: «Число есть множество единиц». Это определение числа математики признавали за наиболее верное до XVIII в. Нуль и дроби по этому определению к числам не относились. Нуль в то время определяли как «ничто», так как 1—1=0 и 2—2=0 и т. д., т. е. в результате не было ничего.

Только во второй половине XVIII в. великий английский математик Исаак Ньютон ввел новое определение числа. Он сказал: «Число есть отношение одной величины к другой того же рода, принятой за единицу». Иначе говоря, число стали рассматривать как результат сравнения любой величины с единицей измерения той же величины. Например: число получалось от сравнения, во сколько раз длина данного отрезка больше или меньше меры, принятой за единицу длины. Подобное сравнение можно получить при делении значения одной величины на значение другой величины того же рода. По этому определению дробь заняла вполне определенное положение среди других чисел.

Полноправным числом стали рассматривать и единицу, которая, как и другие числа, могла быть выражена дробью, например, в виде:

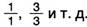
Нуль все еще понимался как знак «ничто». Лишь значительно позже его признали числом, от прибавления или вычитания которого результат не менялся, а при умножении на нуль произведение преобразовывалось в нуль.

Расширение понятия числа на этом не остановилось. Трудами ученых-математиков это понятие продолжало развиваться и обогащаться.