Статистики Ферми-Дирака и Бозе-Эйнштейна.

В распределении Максвелла-Больцмана остается скрытой предпосылка осуществления этого распределения – различимости частиц. Эта предпосылка с физической точки зрения ошибочна, потому что в природе нет различимых частиц, и все реально существующие частицы описываются либо распределением Ферми-Дирака, либо распределением Бозе-Эйнштейна. Однако в наиболее часто встречающихся ситуациях классической физики распределения Ферми-Дирака и Бозе-Эйнштейна практически совпадают с распределением Максвелла-Больцмана, которое благодаря этому является основным распределением классической статистической физики.

Основным понятием квантовой теории, которое играет главную роль в анализе распределения частиц по энергиям, является не понятие о дискретных уровнях энергии, а понятие о квантовых состояниях. Квантовое состояние характеризуется некоторым набором чисел, называемых квантовыми. Некоторые из квантовых чисел могут быть связаны с энергией частицы, а другие с энергией частицы не связаны. Имея одну и ту же энергию, частица может, вообще находиться в различных квантовых состояниях, потому что энергия является лишь одной из характеристик квантового состояния, но далеко не единственной. Различные энергии относятся к различным квантовым состояниям. Частицы в соответствии с правилами поведения распределяются по квантовым состояниям, и в результате этого образуется распределение по энергиям. Частицы неразличимы между собой.

Подсчет числа состояний в статистике Ферми-Дирака. Различаем уровни энергии и различные состояния в пределах одной и той же энергии. Число различных состояний в пределах 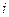-го энергетического уровня 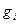, число этих состояний вообще различно для различных энергетических уровней. В этой модели частицы представляются шариками, которые нужно разместить по различным состояниям. Причем в модели Бозе-Эйнштейна в каждом состоянии может быть любое число шаров, а в модели Ферми-Дирака в одном состоянии может быть только один шар. Шары неразличимы между собой. Обозначим число шаров 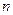и проведем расчет числа возможных размещений шаров для модели Ферми-Дирака.

На каждом энергетическом уровне может находиться 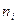частиц, причем 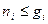. Полное число частиц на всех уровнях равно 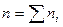. Прежде всего найдем число способов, сколькими 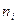не различимых между собой предметов могут быть размещены по 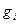местам. Ответ дается формулой, которая для рассматриваемых величин имеет вид: .

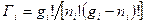На каждом энергетическом уровне микросостояния независимы, и не играет роли, какие именно из частиц, находятся в каком именно состоянии, поэтому полное число состояний в совокупности всех энергетических уровней равно произведению числа микросостояний на каждом отдельном энергетическом уровне. 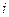- в произведении учитывает все возможные энергетические уровни.

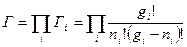- число микросостояний для модели Ферми-Дирака.

Удовлетворяя требование максимума числа микросостояний в равновесном состоянии, являющемся наиболее вероятным состоянием системы получаем формулу:

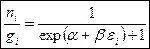- распределения Ферми-Дирака, где 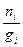- число частиц, приходящихся на одно квантовое состояние с энергией 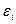. Параметр 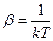. Параметр 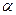определяется нормировкой на полное число частиц, выражающей условие сохранения числа частиц: .

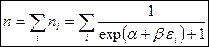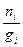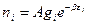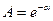При очень малых значениях экспоненциальный член в знаменателе правой части должен быть значительно больше единицы. Поэтому единицей в знаменателе можно пренебречь и записать распределение в виде , где . Если теперь перейти к непрерывному спектру, то получится экспоненциальное распределение Максвелла-Больцмана.

Формулы статистики Ферми-Дирака переходят в формулы статистики Максвелла-Больцмана, когда среднее число частиц, приходящееся на одно квантовое состояние мало.

Подсчет числа состояний в распределении Бозе-Эйнштейна. В модели Бозе-Эйнштейна в каждом квантовом состоянии может находиться произвольное число неразличимых между собой частиц. Как и при выводе распределения Ферми-Дирака, используем понятия энергетических уровней и возможных состояний в пределах отдельного уровня.

При этом условии общее число различных распределений 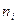частиц по 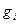местам выражается формулой 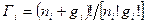. Тогда общее число микросостояний на всех энергетических уровнях:

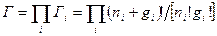- число микросостояний для модели Бозе-Эйнштейна.

Рассуждая так же, как и при выводе распределения Ферми-Дирака получим формулу:

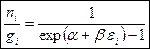- распределения Бозе-Эйнштейна.

Эта формула переходит в распределение Максвелла-Больцмана в случае, когда среднее число частиц, приходящихся на одно квантовое состояние, достаточно мало.

Конкуренция между частицами при занятии состояний в статистике Ферми-Дирака чрезвычайно интенсивна, поскольку занятое какой-либо частицей состояние запрещено для других частиц. Можно в определенном смысле говорить, что частица, занимающая некоторое состояние, отталкивает от этого состояния другие частицы, как бы удерживает из на некотором удалении от этого состояния. Конкуренция между частицами ослабевает, когда число допустимых для них состояний много больше числа частиц.

В статистике Бозе-Эйнштейна такая конкуренция отсутствует: частица может занять некоторое состояние независимо от того. Занято ли оно другими частицами или свободно. Ясно, что если конкуренция в статистике Ферми-Дирака ослабевает, то ее результаты должны приближаться к результатам статистике Бозе-Эйнштейна. Это наблюдается при малом среднем числе частиц, приходящихся на одно квантовое состояние. В этом случае распределения Ферми-Дирака и Бозе-Эйнштейна совпадают и сводятся к распределению Максвелла-Больцмана.