Энтропия. Свободная энергия. Энтальпия.
Второе начало ТД.
Второе начало ТД так же как и I начало ТД является эмпирическим законом, полученным в результате обобщения многолетних опытных результатов. Второе начало ТД было сформулировано, независимо друг от друга двумя учеными, Клаузиусом и Кельвином (лордом Томпсоном).
Формулировка Клаузиуса: процесс, при котором не происходит никаких изменений, кроме передачи тепла от горячего тела к холодному, является необратимым, иначе говоря, теплота не может спонтанно перейти от более холодного тела к более горячему, без каких либо других изменений в системе. (т.е. невозможен циклический процесс, единственным результатом которого является передача тепла от более холодного тела к более горячему телу, без изменений в окружающих телах).
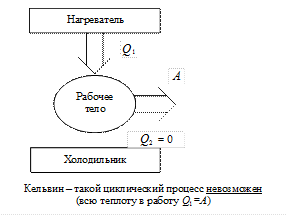 Формулировка Кельвина: Невозможен циклический процесс, единственным результатом которого было бы превращение теплоты, получаемой системой от внешней среды в работу, без изменений в окружающей среде.
Формулировка Кельвина: Невозможен циклический процесс, единственным результатом которого было бы превращение теплоты, получаемой системой от внешней среды в работу, без изменений в окружающей среде.
В этих формулировках ничего не говорится о полном преобразовании работы в теплоту. Действительно, никаких ограничений на этот процесс не существует! Работу можно полностью преобразовать в теплоту без каких-либо иных наблюдаемых изменений (например, торможение автомобиля).
Именно здесь мы встречаемся с фундаментальной ассиметрией природы: работа и теплота, будучи эквивалентными, в качестве возможных способов передачи энергии, все же не вполне эквивалентны с точки зрения из взаимных переходов друг в друга. Эта ассиметрия и выражается II началом ТД.
На первый взгляд формулировки Кельвина и Клаузиуса различны, но они эквивалентны, и если верна одна, то верна и вторая и наоборот, если верна вторая то, следовательно, верна и первая. Докажем эквивалентность формулировок Кельвина и Клаузиуса от противного.
1) Допустим, что Кельвин – неправ, а Клаузиус - прав.
Поместим устройство, работающее против принципа Кельвина, между нагревателем и холодильником. Оно превращает тепло 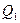 в работу
в работу 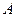 полностью, не производя никаких изменений в окружающей среде.
полностью, не производя никаких изменений в окружающей среде.
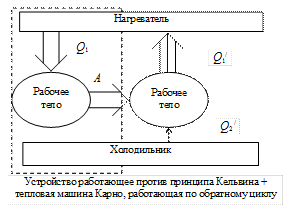 Соединим устройство с тепловой машиной Карно, работающей по обратному циклу, т.е. над рабочим телом совершается работа
Соединим устройство с тепловой машиной Карно, работающей по обратному циклу, т.е. над рабочим телом совершается работа 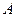 , и рабочее тело, забирая количество теплоты
, и рабочее тело, забирая количество теплоты 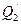 от холодильника, передает
от холодильника, передает 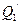 к нагревателю. Предположим, устройство работает достаточно долго. Вся отбираемая у нагревателя теплота
к нагревателю. Предположим, устройство работает достаточно долго. Вся отбираемая у нагревателя теплота 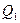 превращается в работу
превращается в работу 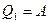 . Затем по закону сохранения энергии тепловая машина Карно передает нагревателю количество теплоты
. Затем по закону сохранения энергии тепловая машина Карно передает нагревателю количество теплоты 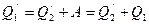 . Очевидно, результатом работы такого устройства является передача количества теплоты
. Очевидно, результатом работы такого устройства является передача количества теплоты 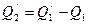 от холодильника нагревателю, без каких-либо изменений в окружающей среде.
от холодильника нагревателю, без каких-либо изменений в окружающей среде.
Мы получили противоречие - устройство, работающее против принципа Клаузиуса, следовательно, доказали, что если Кельвин – неправ, то и Клаузиус – неправ.
2) Допустим, что Клаузиус - неправ, а Кельвин – прав.
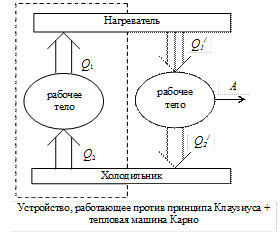 Поместим устройство, работающее против принципа Клаузиуса, между нагревателем и холодильником. Оно передает от холодильника количество теплоты
Поместим устройство, работающее против принципа Клаузиуса, между нагревателем и холодильником. Оно передает от холодильника количество теплоты 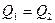 нагревателю без каких-либо изменений в окружающей среде. К этим же термостатам подсоединим тепловую машину Карно. Она берет от нагревателя количество теплоты
нагревателю без каких-либо изменений в окружающей среде. К этим же термостатам подсоединим тепловую машину Карно. Она берет от нагревателя количество теплоты 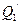 и совершая работу
и совершая работу 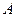 передает холодильнику количество теплоты
передает холодильнику количество теплоты 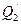 . Предположим, устройство работает достаточно долго. От холодильника забирается количество теплоты
. Предположим, устройство работает достаточно долго. От холодильника забирается количество теплоты 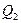 , и передается нагревателю
, и передается нагревателю 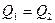 . От нагревателя забирается количество теплоты
. От нагревателя забирается количество теплоты 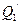 , совершается работа и возвращается холодильнику
, совершается работа и возвращается холодильнику 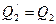 . По закону сохранения энергии
. По закону сохранения энергии 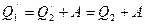 . Очевидно, единственным результатом работы такого устройства будет превращения количества теплоты
. Очевидно, единственным результатом работы такого устройства будет превращения количества теплоты 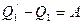 в работу без каких-либо изменений в окружающей среде. Мы получили противоречие - устройство, работающее против принципа Кельвина, следовательно, доказали, что если Клаузиус – неправ, то и Кельвин – неправ.
в работу без каких-либо изменений в окружающей среде. Мы получили противоречие - устройство, работающее против принципа Кельвина, следовательно, доказали, что если Клаузиус – неправ, то и Кельвин – неправ.
Мы доказали эквивалентность формулировок II начала ТД, данных Кельвином и Клаузиусом. Это не единственные формулировки II начала ТД.
Вторая формулировка: невозможен вечный двигатель второго рода, т.е. невозможен двигатель с КПД=100%, который тепло переводит в работу, без каких-либо изменений в окружающей среде.
По Кельвину: 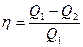 невозможен цикл с
невозможен цикл с 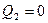 ,
, 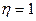 .
.
По Клаузиусу: невозможен цикл 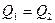 ,
, 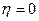 .
.
I начало ТД: 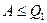 - работа не больше количества тепла, переданного системе.
- работа не больше количества тепла, переданного системе.
II начало ТД: 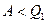 - работа меньше количества тепла, переданного системе.
- работа меньше количества тепла, переданного системе.
Энтропия. Свободная энергия. Энтальпия.
Рассмотрим подробно функции состояния ТД системы и их значение для описания калорических свойств систем. Еще раз отметим, что это величины являются полными дифференциалами от своих параметров, т.е. их изменение зависит только от состояния, а не от пути перехода между этими состояниями. Изменение функции состояния в циклическом процессе равно нулю по определению.
I.) Энтропия.
Рассмотрим цикл Карно. Пусть одна тепловая машина работает с идеальным газом, а другая с другим рабочим телом, причем температуры нагревателей 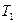 и холодильников
и холодильников 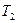 этих машин равны. По I теореме Карно КПД этих машин равны и не зависят от природы рабочего вещества.
этих машин равны. По I теореме Карно КПД этих машин равны и не зависят от природы рабочего вещества. 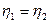 Þ
Þ 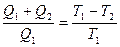 , отметим, что
, отметим, что 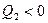 , тогда
, тогда
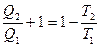 Þ
Þ 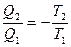 Þ
Þ 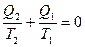 .
.
Получили важный результат. Оказывается, что если 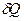 не является функцией состояния, и за цикл не равна нулю
не является функцией состояния, и за цикл не равна нулю 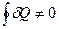 , то приведенная теплота
, то приведенная теплота 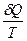 уже является функцией состояния, т.е. на замкнутом цикле ее изменение равно нулю. У понятия «приведенная теплота» нет наглядного примера, его трудно как-то представить.
уже является функцией состояния, т.е. на замкнутом цикле ее изменение равно нулю. У понятия «приведенная теплота» нет наглядного примера, его трудно как-то представить.
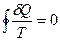
| - данное тождество называется тождеством Клаузиуса, оно справедливо только для обратимых процессов. |
Отсюда следует:
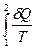
| - для любого обратимого процесса не зависит от пути, и, следовательно, является функцией состояния. |
Эту функцию назвали энтропия. От греческого «энтропос» - возвращение, поворот. Каждое состояние тела характеризуется определенным значением энтропии 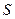 , подобно тому, как оно характеризуется определенным значением внутренней энергии
, подобно тому, как оно характеризуется определенным значением внутренней энергии 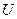 .
.
По определению в интегральной форме 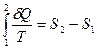
или в дифференциальной форме 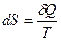 , Þ
, Þ 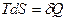 .
.
Тождество Клаузиуса говорит, что при замкнутых обратимых процессах энтропия не меняется.
I начало ТД для обратимых процессов можно записать: 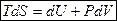 , его еще называют основное ТД тождество.
, его еще называют основное ТД тождество.
Рассмотрим, что происходит при необратимых процессах. Возьмем необратимый цикл Карно, для него КПД меньше, чем у обратимого цикла, т.е.
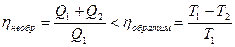 Þ
Þ 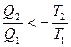 Þ
Þ 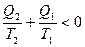 - для необратимых процессов изменение отрицательно. Если обобщать для случая кругового процесса:
- для необратимых процессов изменение отрицательно. Если обобщать для случая кругового процесса:
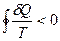
| - неравенство Клаузиуса, для необратимых процессов. |
Как изменяется энтропия в необратимых процессах? Рассмотрим циклический процесс. Из состояния 1 в состояние 2 система перешла по необратимому процессу, а из состояния 2 в состояние 1 по другому обратимому процессу.
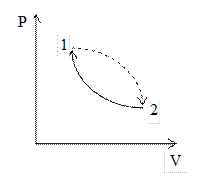 Имеем
Имеем 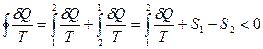
отсюда 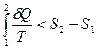 Þ
Þ 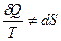 Þ
Þ 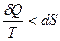
Пусть система изолирована, нет обмена энергией с внешней средой 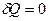 , т.е. наше неравенство в левой части станет равным нулю.
, т.е. наше неравенство в левой части станет равным нулю.
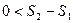 Þ
Þ 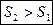
В необратимых процессах для замкнутых систем энтропия возрастает. Мы полагали 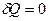 ! Если система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом.
! Если система обменивается теплотой с внешней средой, то ее энтропия может вести себя любым образом.
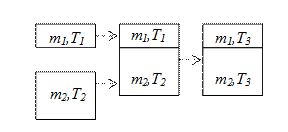 Рассмотрим еще один пример теплопередачу
Рассмотрим еще один пример теплопередачу 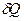 от одного тела к другому. Соприкоснулись два тела.
от одного тела к другому. Соприкоснулись два тела. 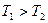 .
.
Тело 1 отдало 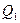 ,
,  ;
;
тело 2 приняло 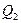 ,
, 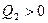 ;
; 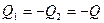 . Объединим оба тела в систему и посмотрим, что стало с энтропией, отметим, что энтропия величина аддитивная:
. Объединим оба тела в систему и посмотрим, что стало с энтропией, отметим, что энтропия величина аддитивная:
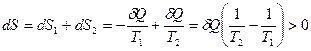
Убеждаемся, что при теплообмене (необратимый процесс), т.е. при передаче количества теплоты от более горячего тела к более холодному, энтропия увеличивается. Реальные необратимые процессы идут таким образом, что изменение энтропии должно быть положительным.
Т.к. 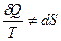 , следовательно, энтропия отличает обратимые и необратимые процессы, показывает направления реальных процессов.
, следовательно, энтропия отличает обратимые и необратимые процессы, показывает направления реальных процессов.
Для необратимых, неравновесных процессов тождество Клаузиуса превращается в неравенство: 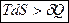 Þ
Þ 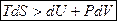
- это неравенство Клаузиуса для необратимых процессов, которое при полном рассмотрении всех потерь теплоты и работы тоже превращается в равенство.
Еще одна формулировка II начала ТД:
Энтропия замкнутой системы в необратимых процессах возрастает. В обратимых процессах остается постоянной. Т.о. для обратимого цикла 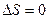 ; для необратимого цикла в изолированных системах
; для необратимого цикла в изолированных системах 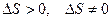 .
.
Что же важно:
Энергия сохраняется, поэтому она не может указывать направление процессов. Все реальные процессы необратимы, поэтому в замкнутых системах они идут в направлении возрастания энтропии. Т.о. энтропия указывает направление реальных процессов. Рост энтропии означает все большую недоступность превращения тепла в работу. Максимум энтропии соответствует состоянию равновесия.
Энтропия экстенсивная величина, она пропорциональна количеству вещества. 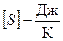 .
.
Энтропия обладает свойством аддитивности: энтропия системы равна сумме энтропий тел, входящих в систему. Этим свойством так же обладают внутренняя энергия, масса, …. Не обладают этим свойством давление, температура. Физический смысл имеет не сама энтропия, а ее изменение.
Обратимые адиабатические процессы, для которых 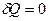 , характеризуются постоянной энтропией
, характеризуются постоянной энтропией 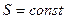 , поэтому их можно назвать изоэнтропийные.
, поэтому их можно назвать изоэнтропийные.
Отметим, что более глубокий смысл энтропии вскрывается в статистической физике. Там энтропия связана с понятием термодинамической вероятности состояния системы.
Получим выражение для энтропии - функции состояния одного моля идеального газа. Используем основное ТД тождество, и термическое уравнение состояния идеального газа:
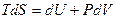 Þ
Þ 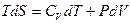 , учтем
, учтем 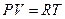
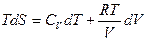 Þ
Þ 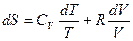 проинтегрировав, получим общее решение,
проинтегрировав, получим общее решение,
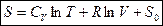 , где
, где 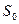 - уровень отсчета энтропии.
- уровень отсчета энтропии.
Мы убедились, что энтропия идеального газа является функцией 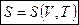 .
.
Рассчитаем изменение энтропии при выравнивании температуры двух тел, приведенных в тепловой контакт. Вычисления будут основываться на том, что энтропия является функцией состояния.
Если система перешла из одного состояния в другое посредством необратимого процесса, то логично мысленно перевести систему из первого состояния во второе с помощью некоторого обратимого процесса и рассчитать происходящее при этом изменение энтропии. Оно равно изменению энтропии при необратимом процессе.
Обозначим массы удельные теплоемкости при постоянном объеме, и температуры первого и второго тел соответственно 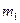 ,
, 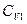 ,
, 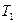 и
и 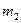 ,
, 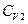 ,
, 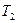 . При тепловом контакте температуры выравниваются. Будем считать для упрощения расчета, что теплообмен происходить при постоянном объеме
. При тепловом контакте температуры выравниваются. Будем считать для упрощения расчета, что теплообмен происходить при постоянном объеме 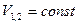 каждого из тел, теплоемкости
каждого из тел, теплоемкости 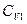 и
и 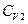 не зависят от температуры,
не зависят от температуры, 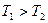 . Тело 1 отдало
. Тело 1 отдало 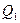 ,
,  ; тело 2 приняло
; тело 2 приняло 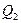 ,
, 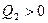 ; Для определения температуры
; Для определения температуры 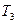 , которую будут иметь тела по достижении термодинамического равновесия, можно написать уравнение
, которую будут иметь тела по достижении термодинамического равновесия, можно написать уравнение 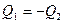 , с учетом I начала ТД:
, с учетом I начала ТД:
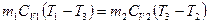 ,
,
отсюда следует, что 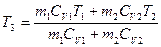
В исходном состоянии тела 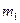 и
и 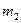 изолированы друг от друга и имеют разные температуры. Затем они приводятся в тепловой контакт. В результате теплообмена тела приходят в состояние 2. Однако переход из состояния 1 в состояние 2 можно совершить также и с помощью обратимых процессов. В этом случае тела
изолированы друг от друга и имеют разные температуры. Затем они приводятся в тепловой контакт. В результате теплообмена тела приходят в состояние 2. Однако переход из состояния 1 в состояние 2 можно совершить также и с помощью обратимых процессов. В этом случае тела 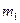 и
и 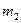 считаются изолированными, и каждое из них обратимым процессом приводится в состояние 2 при одинаковой температуре
считаются изолированными, и каждое из них обратимым процессом приводится в состояние 2 при одинаковой температуре 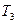 . После этого они приводятся в контакт, но это никакого изменения в их состояния не вносит. Таким образом, в обоих случаях начальное и конечное состояния одинаковы, и изменение энтропии можно просчитать с помощью обратимого процесса по формуле определения энтропии:
. После этого они приводятся в контакт, но это никакого изменения в их состояния не вносит. Таким образом, в обоих случаях начальное и конечное состояния одинаковы, и изменение энтропии можно просчитать с помощью обратимого процесса по формуле определения энтропии:
 , где
, где 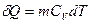 .
.
Вычислив интегралы, получим:
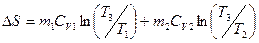 - это и есть изменение энтропии в необратимом процессе теплопередачи при постоянном объеме.
- это и есть изменение энтропии в необратимом процессе теплопередачи при постоянном объеме.
II.) Энтальпия.
Рассмотрим термодинамическую систему, совершающую изобарический процесс.
В этом процессе 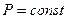 , и тогда давление в выражении для работы можно, как константу, внести под знак дифференциала в приращении объема
, и тогда давление в выражении для работы можно, как константу, внести под знак дифференциала в приращении объема 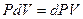 . Учтем это и запишем I начало ТД:
. Учтем это и запишем I начало ТД:
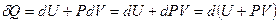 , Þ
, Þ 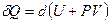 .
.
Правая часть выражения является полным дифференциалом функции  . Это функция получила специальное название - энтальпия
. Это функция получила специальное название - энтальпия 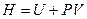 , видим, что
, видим, что 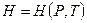 . Еще эту функцию называют «теплосодержание» или «тепловая функция». Изменение энтальпии при переходе из одного состояния в другое зависит только от начального и конечного состояния и не зависит от процесса перехода между ними.
. Еще эту функцию называют «теплосодержание» или «тепловая функция». Изменение энтальпии при переходе из одного состояния в другое зависит только от начального и конечного состояния и не зависит от процесса перехода между ними.
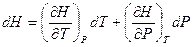
I начало ТД с введением функции «энтальпия» запишется проще: 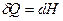 , т.е. изменение энтальпии в изобарическом процессе равно сообщаемому системе количеству теплоты. Энтальпия системы
, т.е. изменение энтальпии в изобарическом процессе равно сообщаемому системе количеству теплоты. Энтальпия системы 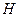 играет ту же роль в процессах при
играет ту же роль в процессах при 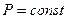 , какую внутренняя энергия
, какую внутренняя энергия 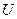 играет в процессах при
играет в процессах при 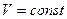 .
.
Выразим теплоемкость системы в изобарическом процессе 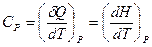 .
.
Учтем 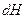 , и что
, и что 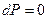 :
: 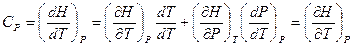 , Þ
, Þ 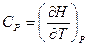
Для нагревания при 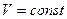 :
: 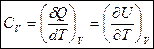 .
.
Для нагревания при 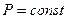 :
:  .
.
Эти соотношения справедливы для любого вещества, а в случаях идеального газа 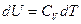 ;
; 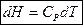 - определяют изменения внутренней энергии и энтальпии в любых процессах, независимо от того, является ли объем и давление постоянными.
- определяют изменения внутренней энергии и энтальпии в любых процессах, независимо от того, является ли объем и давление постоянными.
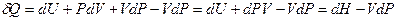 , т.о. в общем случае
, т.о. в общем случае
I начало ТД: 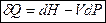 .
.
III.) Свободная энергия.
Рассмотрим термодинамическую систему, совершающую адиабатическое расширение. В таком процессе работа совершается за счет убыли внутренней энергии 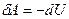 . Можно сказать, что внутренняя энергия характеризует способность системы совершать работу при адиабатическом расширении.
. Можно сказать, что внутренняя энергия характеризует способность системы совершать работу при адиабатическом расширении.
Иначе обстоят дела в случае изотермического расширения. В таком процессе 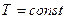 . Внутреннюю энергию использовать для характеристики способности системы совершать работу нельзя, т.к.
. Внутреннюю энергию использовать для характеристики способности системы совершать работу нельзя, т.к.  . Это побуждает нас отличать общую энергию, которой обладает система тел или тело, от той ее части, которую при данных условиях можно использовать для получения работы. Нужно найти другую функцию, которая характеризует работу и является функцией состояния.
. Это побуждает нас отличать общую энергию, которой обладает система тел или тело, от той ее части, которую при данных условиях можно использовать для получения работы. Нужно найти другую функцию, которая характеризует работу и является функцией состояния.
Та часть энергии системы, которая при данных условиях может быть использована для преобразования в механическую работу, называется свободная энергия 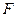 . В обратимых изотермических процессах свободная энергия характеризует способность системы совершать работу. Работа в таких процессах совершается за счет убыли свободной энергии
. В обратимых изотермических процессах свободная энергия характеризует способность системы совершать работу. Работа в таких процессах совершается за счет убыли свободной энергии 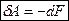 .
.
При изотермическом расширении, когда работа положительна, то свободная энергия убывает, и наоборот при сжатии работа отрицательна, а свободная энергия возрастает, за счет внешних сил, сжимающих тело. Система не может совершить работу, превышающую ее свободную энергию.
В механике энергия тела равна сумме потенциальной и кинетической энергий. Оба этих вида энергий макроскопических тел могут быть полностью преобразованы в механическую работу. Внутренняя энергия молекулярной системы, в интересующем нас случае, не может быть целиком превращена в работу. Посмотрим, чем отличаются 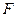 и
и 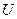 . При изотермическом расширении идеального газа от объема
. При изотермическом расширении идеального газа от объема 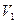 до объема
до объема 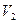 работа одного моля
работа одного моля 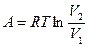 . Правая часть представляет собой убыль свободной энергии
. Правая часть представляет собой убыль свободной энергии 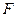 , и она тем больше, чем больше отношение объемов, т.е. чем сильнее сжат газ. А, напомним, внутренняя энергия идеального газа не зависит от объема.
, и она тем больше, чем больше отношение объемов, т.е. чем сильнее сжат газ. А, напомним, внутренняя энергия идеального газа не зависит от объема.
В изотермическом процессе сжатый газ совершает работу за счет подводимого тепла, но мы говорим о свободной энергии газа, т.к. работу совершает газ.
В общем случае, когда процесс протекает необратимо, совершаемая работа меньше чем в обратимом процессе, т.е. меньше чем изменение свободной энергии. 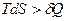 Þ
Þ 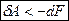 .
.
Возможны так же случаи, когда изменение свободной энергии не сопровождается совершением работы, например, расширение газа в пустоту. Работ не совершается, внутренняя энергия не изменяется, а способность совершать работу падает. Это так, потому что процесс расширения газа в пустоту необратим полностью, хотя и изотермический.
Свободная энергия 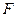 , так же как и внутренняя энергия является функцией состояния системы. А это вытекает из того, что при обратимом изотермическом процессе, при переходе из состояния 1 в состояние 2 и обратно в 1, работа
, так же как и внутренняя энергия является функцией состояния системы. А это вытекает из того, что при обратимом изотермическом процессе, при переходе из состояния 1 в состояние 2 и обратно в 1, работа 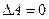 , следовательно, в таком переходе работа не зависит от пути, а только от начального и конечного состояния системы.
, следовательно, в таком переходе работа не зависит от пути, а только от начального и конечного состояния системы.
Рассмотрим I начало для изотермического процесса 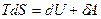 ,
, 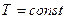 Þ
Þ 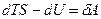 Þ
Þ 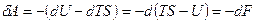 .
.
Мы нашли выражение для функции свободной энергии 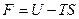 Þ
Þ 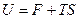 .
.
Внутренняя энергия системы состоит из суммы свободной 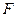 и связанной
и связанной 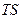 энергий системы. Свободную энергию можно рассматривать как потенциальную энергию системы, находящуюся при постоянных температуре и давлении
энергий системы. Свободную энергию можно рассматривать как потенциальную энергию системы, находящуюся при постоянных температуре и давлении 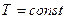 и
и 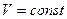 . Поэтому условием равновесия ТД системы будет условие минимума свободной энергии.
. Поэтому условием равновесия ТД системы будет условие минимума свободной энергии.
Если в системе 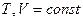 , то в системе могут идти только такие процессы, которые приводят к уменьшению свободной энергии в случае необратимых процессов, или оставляют неизменной свободную энергию в обратимых процессах.
, то в системе могут идти только такие процессы, которые приводят к уменьшению свободной энергии в случае необратимых процессов, или оставляют неизменной свободную энергию в обратимых процессах.
| <== предыдущая лекция | | | следующая лекция ==> |
| Цикл Карно. Теоремы Карно. | | | Термодинамические потенциалы. Метод термодинамических потенциалов. |
Дата добавления: 2019-10-16; просмотров: 830;
