Принадлежность точки и линии поверхности

Ограничив призматическую поверхность двумя параллельными между собой плоскостями, пересекающими образующие, получаем призму. Ограничив пирамидальную поверхность одной плоскостью, будем иметь пирамиду. Тогда эти секущие плоскости называются основаниями многогранника, а образующие поверхности – боковыми поверхностями.

Рассмотрение образования боковых поверхностей многогранников с использованием таких понятий, как образующая и направляющая, играет большую роль в решении задач начертательной геометрии.

Построение любых проекций точек на поверхности многогранника осуществляется наиболее эффективно при помощи образующих и направляющих, хотя можно использовать и другие приемы.

Как правило, задача формулируется следующим образом: по двум проекциям многогранника построить третью и начертить недостающие проекции точки или линии на его поверхности.

Рассмотрим пример.

Пусть заданы фронтальная и горизонтальная проекции наклонной призмы. Требуется построить отсутствующие проекции точек на ее поверхности, если на чертеже (рис.3.7) есть точки 1₂, (2₁), (3₁), 4₁, (5₂).

Построим последовательно отсутствующие проекции точек.

Рис. 3.7. Построение точек на поверхности призмы.

Так как точка 1₂ лежит на ребре Е₂Е₂*, то 1₁ – на ребре Е₁*Е₁, что позволяет получить ее по линии связи. Поскольку ребро Е₁Е₁* невидимое, то и (1₁) – невидимая.

Точка (2₁) – невидимая, значит она принадлежит грани Е₁*Е₁ D₁D₁*. Проводим через нее образующую, параллельную любому боковому ребру, до пересечения с основанием. Затем по линии связи получаем фронтальную проекцию точки на основании (на ребре Е₂*D₂*), после чего проводим через эту точку образующую и на ней по линии связи от (2₁) находим 2₂. Поскольку на фронтальной проекции грань Е₂*Е₂ D₂ D₂* видимая, то и точка 2₂ видимая.

Так как точка 3₁ невидимая, то она лежит на основании А₁*В₁*С₁*D₁*Е₁*. Следовательно, точка 3₂ строится по линии связи, ведь на П₂ основание призмы представляет собой прямую А₂*В₂*С₂*D₂*Е₂*.

Используя описанный принцип можно построить остальные проекции (4₂), 5₁.

Рассмотрим достаточно традиционную задачу построения проекций точек, лежащих на поверхности прямой пирамиды (рис. 3.8). Пусть заданы фронтальная и горизонтальная проекции пирамиды SABC и проекции точек 1₂, 2₂, 3₂. Надо построить третью проекцию пирамиды и отсутствующие горизонтальные и профильные проекции точек 1, 2, 3.

Для построения профильной проекции пирамиды через вершину S проведем фронтальную плоскость уровня. Тогда ее горизонтальная Ф₁ и профильная Ф₃ проекции будут служить базовыми линиями взамен традиционных осей проекций ОХ и ОY. Точку S₃ получаем по линиям связи на базовой линии. Затем определяем положение точек А₃=С₃ и В₃, откладывая от базовой линии Ф₃ отрезки , равные расстояниям от А₁, С₁, В₁ до Ф₁ соответственно. Соединив точки основания вершиной, получаем профильную проекцию пирамиды. Как видим, грань SAC на профильной плоскости проекций вырождается в линию S₃A₃ ( или S₃C₃).

Решим вторую часть задачи – построение отсутствующих проекций точек 1, 2, 3. Для определения положения горизонтальной проекции 1₁ используем образующую пирамиды: проведем через вершину S₂ и точку 1₂ прямую до пересечения с ребром А₂В₂ основания. Затем по линии связи получим горизонтальную проекцию этой точки на ребре А₁В₁. Соединив полученную точку с вершиной S₁, будем иметь горизонтальную проекцию образующей. На ней и лежит точка 1₁, положение которой определим по линии связи 1₂. Аналогично можно построить горизонтальную проекцию 2₁, с учетом того, что (2₂) – невидимая. Значит точка 2 лежит на грани SAC. Тогда основание образующей попадает на ребро АС основания. В остальном построения полностью повторяют предыдущие.

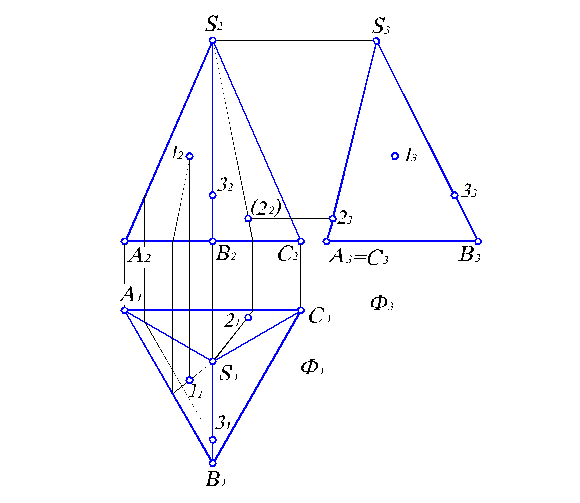
Рис. 3.8. Построение точек на поверхности пирамиды.

Однако для определения положения горизонтальной проекции 3₁ использовать образующую не представляется возможным, так как ребро SB, на котором лежит точка 3, в проекциях на П₁, П₂ дает вертикальную прямую (т.е. является профильной линией уровня). В этом случае используют линию, параллельную основанию. Через точку 3₂ проводят прямую, параллельную А₂В₂, до пересечения с ребром S₂A₂. Затем на ребре S₁A₁ по линии связи получают горизонтальную проекцию точки пересечения, через которую проводят прямую параллельно А₁В₁. Поскольку точка 3 лежит на этой прямой, то продолжая ее горизонтальную проекцию до пересечения с ребром S₁В₁, получаем точку 3₁.

Профильную проекцию 1₃ строим на основании взаимосвязи между горизонтальной и профильной проекциями точки. А именно, откладываем по линии связи, проходящей через 1₂, от базовой линии Ф₃ вправо отрезок, равный расстоянию от 1₁ до Ф₁, как это делалось при построении профильной проекции пирамиды. Точка 2₃ лежит на пересечении горизонтальной линии связи, проходящей через 2₂, и грани S₃A₃C₃, превратившейся в прямую S₃A₃. Наконец, точку 3₃ находим на горизонтальной линии связи, проходящей через 3₂ и ребро S₃В₃.

Следует заметить, что горизонтальную проекцию 3₁ можно найти через профильную. Для этого измеряем расстояния от 3₃ до Ф₃ и откладываем его вниз от Ф₁ по ребру S₁В₁.

При использовании базовой линии (взамен осей проекций) необходимо учитывать направление, в котором строятся проекции. Подчеркнем, что когда горизонтальная проекция какой-либо точки расположена ниже Ф₁, профильная проекция этой точки лежит вправо от Ф₃, если горизонтальная проекция выше Ф_1, тогда профильная проекция левее Ф₃. Это достаточно очевидно, так как профильная проекция соответствует взгляду на любую точку (а следовательно, и любой геометрический объект) слева.

Линию на поверхности многогранника можно построить по характерным точкам, которыми являются точки ее изгиба и точки перехода через ребра. При этом следует помнить, что ломаная линия на поверхности многогранника будет ломаной, состоящей из отрезков прямой , в любой плоскости проекций, а кривая – кривой ( за исключением частных случаев).

Рассмотрим примеры.

По фронтальной проекции А₂В₂С₂D₂ ломаной линии, лежащей на поверхности прямой шестигранной призмы (рис. 3.9), построить горизонтальную и профильную проекции.

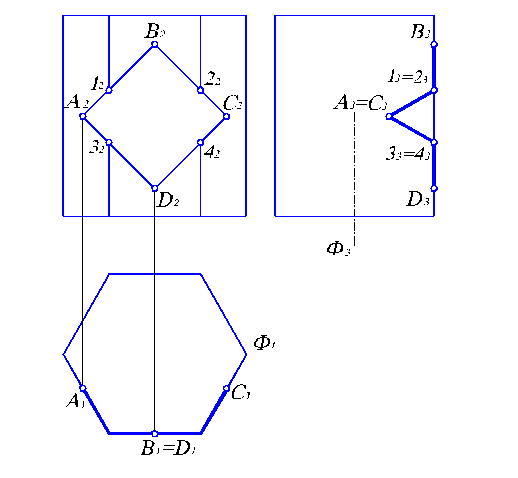
Рис. 3.9. Построение ломаной линии на поверхности призмы.

Поскольку призма прямая и ее боковые ребра являются горизонтально-проецирующими линиями, то на П₁ ее боковые грани вырождаются в отрезки прямой, составляющие ломаную линию (шестиугольник). Следовательно, горизонтальная проекция любой точки боковой поверхности призмы лежит на этом шестиугольнике, в том числе и точки линии А₁В₁С₁D_1..

Для построения профильной проекции А₃В₃С₃D₃ требуется найти промежуточные точки ломаной, лежащие на ребрах призмы. Это точки 1, 2, 3, 4, являющиеся также характерными. По фронтальным проекциям 1₂, 2₂, 3₂, 4₂, найдем профильные проекции 1₃=2₃, 3₃=4₃, используя горизонтальные линии связи. Аналогично строим точки В₃, D₃. Они лежат на том же ребре , т.к. грань, являющаяся фронтальной линией уровня, превращается на П₃ в прямую. Точки А₃, С₃ получаем, откладывая от Ф₃ вправо по линии связи с А₂, С₂ расстояние, отмеренное от А₁, С₁ до Ф₁. Соединяя полученные точки, имеем решение в виде замкнутой ломаной А₃1₃В₃2₃С₃4₃D₃3₃А₃. Заметим, если линия на поверхности многогранника замкнутая, то и все ее проекции замкнутые линии.

Решим следующую задачу. По фронтальной проекции кривой линии, лежащей на поверхности прямой пирамиды, построить горизонтальную и профильную (рис. 3.10).

Рис. 3.10. Построение кривой линии на поверхности пирамиды.

Характерными точками для этой кривой будут точки 1₂, 2₂, 3₂, 4₂, ее пересечения с ребрами S₂B₂, S₂С₂. Промежуточных точек можно выбрать любое количество (чем больше, тем точнее решение): 5₂, 6₂, 7₂, 8₂, 9₂.

Горизонтальные и профильные проекции характерных точек 1₃=2₃ и 3₃=4₃ получим по линиям связи. Далее любую из промежуточных точек построим, используя прямые, параллельные соответствующим ребрам основания. Так, для точки 7₂ эта прямая параллельна С₂D₂, следовательно, на П₁ она параллельна С₁D₁.

По горизонтальным и фронтальным проекциям, используя правило взаимосвязи проекций, строятся профильные проекции. Соединив проекции точек, получим замкнутую кривую 1₃9₃2₃8₃7₃3₃6₃4₃5₃1₃, невидимые участки которой обозначим пунктирной линией.

Таким образом, построение проекций любой, сколь угодно сложной, кривой базируется на построении проекций точек, расположенных на этой кривой.