ОСНОВНЫЕ ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ
| Закон | Для ИЛИ | Для И |
| Переместительный | 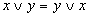
| 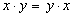
|
| Сочетательный | 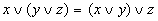
| 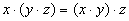
|
| Распределительный | 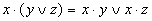
| 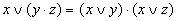
|
| Правила де Моргана | 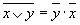
| 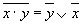
|
| Идемпотенции | 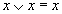
| 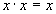
|
| Поглощения | 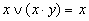
| 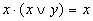
|
| Склеивания | 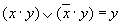
| 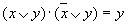
|
| Операция переменной с ее инверсией | 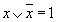
| 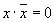
|
| Операция с константами | 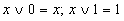
| 
|
| Двойного отрицания | 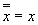
|
5.10. Как составить таблицу истинности?
Согласно определению, таблица истинности логической формулы выражает соответствие между всевозможными наборами значений переменных и значениями формулы.
Для формулы, которая содержит две переменные, таких наборов значений переменных всего четыре:
(0, 0), (0, 1), (1, 0), (1, 1).
Если формула содержит три переменные, то возможных наборов значений переменных восемь:
(0, 0, 0), (0, 0, 1), (0, 1, 0), (0, 1, 1), (1, 0, 0), (1, 0, 1), (1, 1, 0), (1, 1, 1).
Количество наборов для формулы с четырьмя переменными равно шестнадцати и т.д.
Удобной формой записи при нахождении значений формулы является таблица, содержащая кроме значений переменных и значений формулы также и значения промежуточных формул.
Примеры.
1. Составим таблицу истинности для формулы 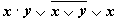 , которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу:
, которая содержит две переменные x и y. В первых двух столбцах таблицы запишем четыре возможных пары значений этих переменных, в последующих столбцах — значения промежуточных формул и в последнем столбце — значение формулы. В результате получим таблицу:
| Переменные | Промежуточные логические формулы | Формула | |||||
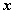
| 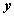
| 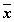
| 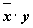
| 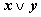
| 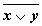
| 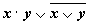
| 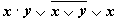
|
Из таблицы видно, что при всех наборах значений переменных x и y формула 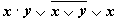 принимает значение 1, то есть является тождественно истинной.
принимает значение 1, то есть является тождественно истинной.
2. Таблица истинности для формулы 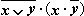 :
:
| Переменные | Промежуточные логические формулы | Формула | ||||
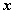
| 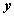
| 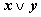
| 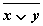
| 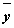
| 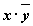
| 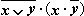
|
Из таблицы видно, что при всех наборах значений переменных x и y формула 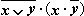 принимает значение 0, то есть является тождественно ложной.
принимает значение 0, то есть является тождественно ложной.
3. Таблица истинности для формулы 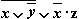 :
:
| Переменные | Промежуточные логические формулы | Формула | ||||||
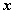
| 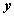
| 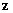
| 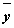
| 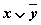
| 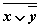
| 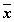
| 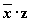
| 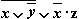
|
Из таблицы видно, что формула 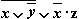 в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.
в некоторых случаях принимает значение 1, а в некоторых — 0, то есть является выполнимой.
5.11. Как упростить логическую формулу?
Равносильные преобразования логических формул имеют то же назначение, что и преобразования формул в обычной алгебре. Они служат для упрощения формул или приведения их к определённому виду путем использования основных законов алгебры логики.
| Под упрощением формулы, не содержащей операций импликации и эквиваленции, понимают равносильное преобразование, приводящее к формуле, которая либо содержит по сравнению с исходной меньшее число операций конъюнкции и дизъюнкции и не содержит отрицаний неэлементарных формул, либо содержит меньшее число вхождений переменных. |
Некоторые преобразования логических формул похожи на преобразования формул в обычной алгебре (вынесение общего множителя за скобки, использование переместительного и сочетательного законов и т.п.), тогда как другие преобразования основаны на свойствах, которыми не обладают операции обычной алгебры (использование распределительного закона для конъюнкции, законов поглощения, склеивания, де Моргана и др.).
Покажем на примерах некоторые приемы и способы, применяемые при упрощении логических формул:
1) 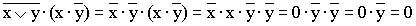
(законы алгебры логики применяются в следующей последовательности: правило де Моргана, сочетательный закон, правило операций переменной с её инверсией и правило операций с константами);
2) 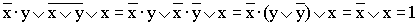
(применяется правило де Моргана, выносится за скобки общий множитель, используется правило операций переменной с её инверсией);
3) 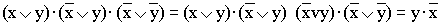
(повторяетсявторойсомножитель, что разрешено законом идемпотенции; затем комбинируются два первых и два последних сомножителя и используется закон склеивания);
4) 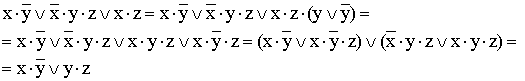
(вводится вспомогательный логический сомножитель (  ); затем комбинируются два крайних и два средних логических слагаемых и используется закон поглощения);
); затем комбинируются два крайних и два средних логических слагаемых и используется закон поглощения);
5) 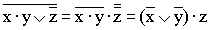
(сначаладобиваемся, чтобы знак отрицания стоял только перед отдельными переменными, а не перед их комбинациями, для этого дважды применяем правило де Моргана; затем используем закон двойного отрицания);
6) 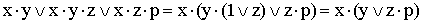
(выносятся за скобки общие множители; применяется правило операций с константами);
7) 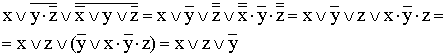
(к отрицаниям неэлементарных формул применяется правило де Моргана; используются законы двойного отрицания и склеивания);
8) 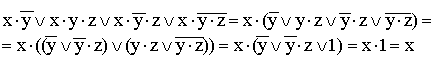
(общий множитель x выносится за скобки, комбинируются слагаемые в скобках — первое с третьим и второе с четвертым, к дизъюнкции 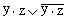 применяется правило операции переменной с её инверсией);
применяется правило операции переменной с её инверсией);
9) 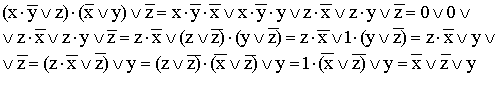
(используются распределительный закон для дизъюнкции, правило операции переменной с ее инверсией, правило операций с константами, переместительный закон и распределительный закон для конъюнкции);
10) 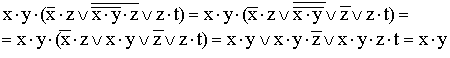
(используются правило де Моргана, закон двойного отрицания и закон поглощения).
Из этих примеров видно, что при упрощении логических формул не всегда очевидно, какой из законов алгебры логики следует применить на том или ином шаге. Навыки приходят с опытом.
5.12. Что такое переключательная схема?
В компьютерах и других автоматических устройствах широко применяются электрические схемы, содержащие сотни и тысячи переключательных элементов: реле, выключателей и т.п. Разработка таких схем весьма трудоёмкое дело. Оказалось, что здесь с успехом может быть использован аппарат алгебры логики.
| Переключательная схема — это схематическое изображение некоторого устройства, состоящего из переключателей и соединяющих их проводников, а также из входов и выходов, на которые подаётся и с которых снимается электрический сигнал. |
Каждый переключатель имеет только два состояния: замкнутое и разомкнутое. Переключателю Х поставим в соответствие логическую переменную х, которая принимает значение 1 в том и только в том случае, когда переключатель Х замкнут и схема проводит ток; если же переключатель разомкнут, то х равен нулю.
Будем считать, что два переключателя Х и  связаны таким образом, что когда Х замкнут, то
связаны таким образом, что когда Х замкнут, то  разомкнут, и наоборот. Следовательно, если переключателю Х поставлена в соответствие логическая переменная х, то переключателю
разомкнут, и наоборот. Следовательно, если переключателю Х поставлена в соответствие логическая переменная х, то переключателю  должна соответствовать переменная
должна соответствовать переменная 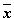 .
.
Всей переключательной схеме также можно поставить в соответствие логическую переменную, равную единице, если схема проводит ток, и равную нулю — если не проводит. Эта переменная является функцией от переменных, соответствующих всем переключателям схемы, и называется функцией проводимости.
Найдем функции проводимости F некоторых переключательных схем:
a) 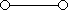
Схема не содержит переключателей и проводит ток всегда, следовательно F=1;
б) 
Схема содержит один постоянно разомкнутый контакт, следовательно F=0;
в) 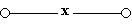
Схема проводит ток, когда переключатель х замкнут, и не проводит, когда х разомкнут, следовательно, F(x) = x;
г) 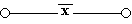
Схема проводит ток, когда переключатель х разомкнут, и не проводит, когда х замкнут, следовательно, F(x) = 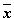 ;
;
д) 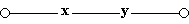
Схема проводит ток, когда оба переключателя замкнуты, следовательно, F(x) = x . y;
е) 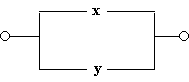
Схема проводит ток, когда хотя бы один из переключателей замкнут, следовательно, F(x)=x v y;
ж) 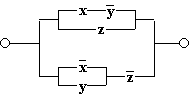
Схема состоит из двух параллельных ветвей и описывается функцией 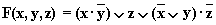 .
.
| Две схемы называются равносильными, если через одну из них проходит ток тогда и только тогда, когда он проходит через другую (при одном и том же входном сигнале). Из двух равносильных схем более простой считается та схема, функция проводимости которой содержит меньшее число логических операций или переключателей. |
Задача нахождения среди равносильных схем наиболее простых является очень важной. Большой вклад в ее решение внесли российские учёные Ю.И. Журавлев, С.В. Яблонский и др.
При рассмотрении переключательных схем возникают две основные задачи: синтез и анализ схемы.
СИНТЕЗ СХЕМЫ по заданным условиям ее работысводится к следующим трём этапам:
- составлению функции проводимости по таблице истинности, отражающей эти условия;
- упрощению этой функции;
- построению соответствующей схемы.
АНАЛИЗ СХЕМЫ сводится к
- определению значений её функции проводимости при всех возможных наборах входящих в эту функцию переменных.
- получению упрощённой формулы.
Примеры.
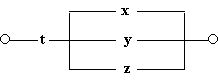
1. Построим схему, содержащую 4 переключателя x, y, z и t, такую, чтобы она проводила ток тогда и только тогда, когда замкнут контакт переключателя t и какой-нибудь из остальных трёх контактов.
Решение. В этом случае можно обойтись без построения таблицы истинности. Очевидно, что функция проводимости имеет вид F(x, y, z, t) = t . (x v y v z), а схема выглядит так:
2. Построим схему с пятью переключателями, которая проводит ток в том и только в том случае, когда замкнуты ровно четыре из этих переключателей.
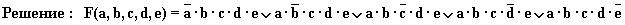
Схема имеет вид:
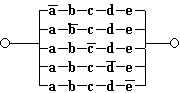
3. Найдем функцию проводимости схемы:
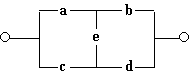
Решение. Имеется четыре возможных пути прохождения тока при замкнутых переключателях a, b, c, d, e : через переключатели a, b; через переключатели a, e, d; через переключатели c, d и через переключатели c, e, b. Функция проводимости F(a, b, c, d, e) = a . b v a . e . d v c . d v c . e . b.
4. Упростим переключательные схемы:
а) 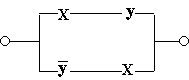
Решение: 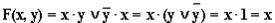
Упрощенная схема: 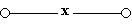
б) 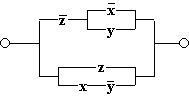
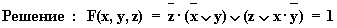 .
.
Здесь первое логическое слагаемое 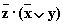 является отрицанием второго логического слагаемого
является отрицанием второго логического слагаемого 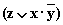 , а дизъюнкция переменной с ее инверсией равна 1.
, а дизъюнкция переменной с ее инверсией равна 1.
Упрощенная схема : 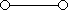
в) 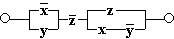
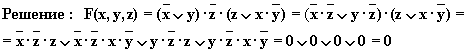
Упрощенная схема: 
г) 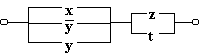
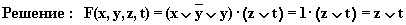
Упрощенная схема: 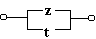
д) 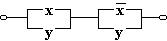
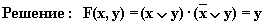 (по закону склеивания)
(по закону склеивания)
Упрощенная схема: 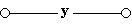
е) 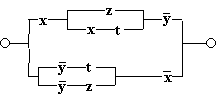
Решение: 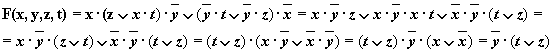
Упрощенная схема: 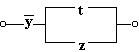
5.13. Как решать логические задачи?
Разнообразие логических задач очень велико. Способов их решения тоже немало. Но наибольшее распространение получили следующие три способа решения логических задач:
- средствами алгебры логики;
- табличный;
- с помощью рассуждений.
Познакомимся с ними поочередно.
Дата добавления: 2019-07-26; просмотров: 1323;
