Фазовая и групповая скорости, фононы

Атомы, находящиеся в узлах кристаллической решетки, при тем­пературе, отличной от абсолютного нуля, совершают колебания в ок­рестности положения равновесия. Носители заряда, движущиеся среди колеблющихся атомов, обмениваются с ними энергией, благодаря че­му устанавливается термодинамическое равновесие между решеткой и электронным газом.

Вследствие сильного межатомного взаимодействия колебание каж­дого атома передается соседним, и в кристалле возбуждаются «коллек­тивные» колебания атомов, распространяющиеся во всевозможных направлениях. Если на атом действует сила, пропорциональная его смещению из положения равновесия, то возникают гармонические ко­лебания. Следовательно, колеблющийся атом можно считать гармониче­ским осциллятором. Колебания каждого гармонического осциллятора можно разложить на составляющие по трем направлениям. Атомы кри­сталла упруго связаны между собой, и колебания любого из них пере­даются соседям. Такие колебания называются нормальными. В кри­сталле, содержащем N атомов, распространяются упругие волны от 3N осцилляторов, т. е. возможно 3N нормальных колебания.

Волновой процесс характеризуется также фазовой и групповой скоростями распространения волны. Фазовая скорость представляет собой скорость перемещения в пространстве точки с заданной фазой .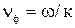

,

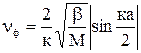где b - жесткость связи, М – масса атома.

Скорость распространения волнового пакета (скорость переноса энергии в среде) определяется групповой скоростью .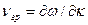

.

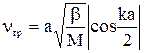Если длина цепочки L, то наиболее длинноволновые колебания, которые могут распространяться в такой цепочке, имеют длину волны λ_max=2L, а наиболее коротковолновые – λ_min=2a. В последнем случае может быть найдена максимально возможная частота колебаний

ω_max=2πν/λ_min=πν/a=κν,

где ν – средняя скорость распространения нормальных колебаний. Отсюда видно, что максимальная частота колебаний является постоянной величиной для каждого конкретного материала. Например, для меди (а≈3,6∙10^{-10 м, ν≈3,6∙103} м/с), ω_max≈3∙10¹³, для окиси цинка (а≈4,7∙10^{-10 м, ν≈2,7∙103} м/с), ω_max≈1,8∙10¹³.

Из соотношений для фазовой и групповой скоростей следует, что для длинных волн (к→0) ν_ф=ν_гр=ν_зв, где ν_зв – средняя скорость распространения звука в кристалле. Для коротких волн (к→π/а) ν_гр→0, ν_ф→( 2а/π)× .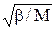

Рассмотрим тепловые колебания решетки с квантовой точки зре­ния. Энергия каждого из 3N колебаний квантована. Разрешенные зна­чения энергии определяются выражением

,

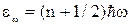где 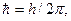h – постоянная Планка, 0,1,2,… Отсюда видно что минимально возможное изменение тепловой энергии равно ħw. Эта минимальная порция, или квант энергии колебания, называется фононом. Если представить решетку в виде фононного газа, то увеличение энергии ε_ω= ε_ω0+∆ε означает увеличение концентрации фононов, уменьшение же энергии ε_ω= ε_ω0 - ∆ε – уменьшение концентрации фононов. При этом акустическим колебаниям решетки соответствуют акустические фононы, оптическим – оптические фононы.