Интегрирование рациональных функций
Напомним основные понятия и утверждения, касающиеся рациональных функций.
Определение. Рациональной функцией переменной 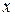 называется отношение двух многочленов этой переменной:
называется отношение двух многочленов этой переменной: 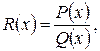 где
где 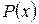 и
и 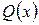 – многочлены переменной
– многочлены переменной 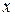 .
.
Теорема. Любая рациональная функция с вещественными коэффициентами может быть представлена в виде суммы цело-рациональной функции, (то есть многочлена) и простейших дробно-рациональных функций 1-го и 2-го рода (то есть функций вида 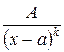 , где
, где 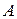 и
и 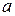 – вещественные числа,
– вещественные числа, 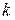 – натуральное число и
– натуральное число и 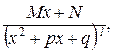
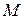 ,
, 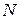 ,
, 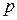 ,
, 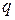 – вещественные числа,
– вещественные числа, 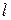 – натуральное число, причем
– натуральное число, причем 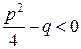 ).
).
Согласно этой теореме и свойству линейности неопределенного интеграла, вычисление неопределенного интеграла от рациональной функции с вещественными коэффициентами сводится к вычислению неопределенных интегралов от цело-рациональной функции и от простейших дробно-рациональных функций 1-го рода и 2-го рода.
а) Рассмотрим неопределенный интеграл от цело-рациональной функции
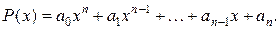
Согласно свойству линейности неопределенного интеграла, имеем:
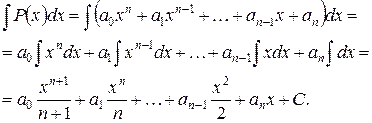
Таким образом, неопределенный интеграл от цело-рациональной функции (многочлена степени 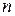 ) есть цело-рациональная функция (многочлен степени
) есть цело-рациональная функция (многочлен степени 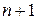 ).
).
б) Рассмотрим неопределенный интеграл от простейшей дробно-рациональной функции 1-го рода 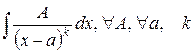 – натуральное число.
– натуральное число.
Пусть 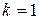
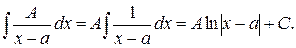
Пусть 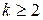 .
.
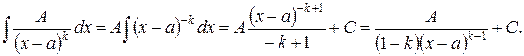
Дата добавления: 2019-07-26; просмотров: 183;
