Пропускная способность двоичного канала

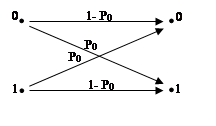
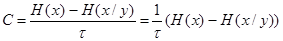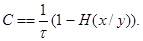
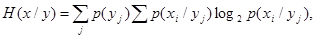
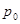- ошибочный переход,

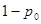- правильный переход.

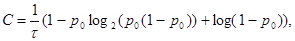
Если p₀=0, то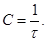

А(t)

t

P()ai=0,т.к. этих самых ai=бесконечность.

Посредством измерительных приборов получается дискретность в измерениях a(t).

H(a)=-∑W(ai)Δa logW(ai)Δa

H(a)=∑W(ai)Δa logΔa∑W(ai) Δa logΔa=(∫W(ai)*logΔa)-logΔa∫W(a)da=

і ª

=∫W(a)logW(a)da-logΔa

ª

-энтропия непрерывного источника.

Теоретически Н(а) непрерывного источника=бесконечность.

Дифференциальная энтропия характеризует количество информации в непрерывном источнике при заданной точности его представления Δа

Моменты времени, в которые снимаются показания непрерывного источника, называются отсчетами.Т.е.h –количество информации в источнике,приходящееся на один

отсчет.[h]=бит/отсчет.

Если в прикладной задаче получается результат в виде разности энтропий,то

H абсолютно точно характеризует колво информации источника.

H Гауссовского источника:

W(a)=1*e(-a/2σ²)²/(√2πσ)

-если источник формирует множество случайных факторов поW(a) получается гауссовский:

H(a)= -∫W(a).[-[(a/2σ)*loge]²]da-log(1/√2π*σ)*∫W(a)da

∫(a)²+W(a)da-loge

H(a)=log(√2πσ)+———————

2σ²³

∞

∫a²W(a)da=σ²

-∞

H(a)=log(√2πσ)+log(√e)

h=log(√2πe*σ)

A(t)-F

F=3400Гц-полоса пропускания отсчетов должно быть 2F в секунду.

h=2F log[√2π(σ²)e]

Бит/сек-количествово информации в одну секунду.

P(ui)=W(ui)du

H(ui,vj)=∑∑p(ui,vj)logp(ui/vj)/p(ui)

Δu-du i j

Δv-dv

H(u,v)=h(u-h(u/v))

H(u,v)=∫∫W(u,v)log[(W(u/v)du)/W(u)du

uv

Для дискретного канала с помехами получим выражение, аналогичное

Выражению непрерывного канала.

H(u,v)=h(v)-h(v/u)

В гауссовском непрерывном канале все законы распределения имеют

Гауссовский характер.

Pn

Pc Pc+Pn-мощность выходного

H=log[√2πσ²e]

h(v)=log[√2πe(Pc+Pn)]

h(v/u)=log(√2πePn)

H(u,v)=0,5log(1+Pc/Pn)

C=Flog(1+Pc/Pn)

-кол-во информации,проходящей по каналу за один отсчет.

-пропускная способность непрерывного канала.

Эпсилон- энтропия.

Ai^(t)-копия(грубое представление источника)

A^i(t)=ai(t)+E(t)-погрешность.

∑∑p(ai,ai^)logp(ai/ai^)/p(ai)=H(ai,ai^)

ai ai^

Δ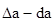
a^-da^

H(a,a^)=∫∫W(a,a^)log(W(a/a^)/W(a))dada^

ªªˆ

T

εo²t=(1∫(a(t)-a^(t))²dt)/T

H(a)ε -минимальная двумерная энтропия источника и его копия при заданной погрешности

H(a)ε=h(a)-h(a/a^)-ошибка

εо(t)-средний квадрат отклонения

Считая,что все статистики-гауссовские

σa²=Pa

σε²=Pε

H(a)ε=log(√Pa/Pε)

-эпсилон-энтропия на один отсчет.

H(a)ε=Flog(Pa/Pε)

-эпсилон-производительность непрерывного источника.

Теорема Шеннона для непрерывного канала

Если

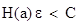
То существует метод кодирования , позволяющий восстановить

Непрерывное сообщение с заданной погрешностью ε