Линейные функционалы
С понятием линейного функционала произошло знакомство в главе IX. Напомним соответствующее определение.
Определение 11.1. Линейный оператор, действующий из любого пространства в поле, над которым оно задано, называется линейным функционалом.
Обозначать линейные функционалы будем малыми греческими буквами. Приведем несколько примеров.
Пример 11.1. Нулевой функционал. Именно, 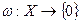 .
.
Пример 11.2. Пусть 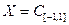 . Функционал
. Функционал 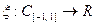 определим соотношением:
определим соотношением:
 , где
, где  .
.
Пример 11.3. Пусть 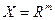 , тогда линейным функционалом будет отображение
, тогда линейным функционалом будет отображение 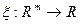 , определяемое равенством
, определяемое равенством 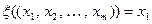 для любого вектора
для любого вектора 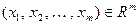 .
.
Определение 11.2. Множество всех линейных функционалов, определенных на линейном пространстве Х, называется пространством, сопряженным к пространству Х. Такое пространство существует по теореме 9.2 и обозначается 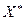 .
.
Определение 11.3. Пусть 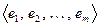 – базис в пространстве Х и
– базис в пространстве Х и 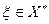 . Тогда числа
. Тогда числа 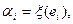
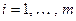 , будем называть коэффициентами функционала
, будем называть коэффициентами функционала 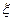 в базисе
в базисе 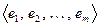 .
.
Для произвольного вектора 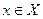 такого, что
такого, что 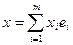 будем иметь
будем иметь
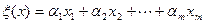 . (11.1)
. (11.1)
Понятно, что значение функционала 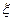 на произвольном векторе пространства в данном базисе определено однозначно.
на произвольном векторе пространства в данном базисе определено однозначно.
Определение 11.4. Выражение (11.1), задающее значение линейного функционала на векторе х в заданном базисе, называется линейной формой, отвечающей данному функционалу.
Линейная форма однозначно определяется базисом 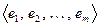 , и поэтому можно было бы записывать ее в виде
, и поэтому можно было бы записывать ее в виде
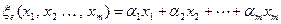 . (11.2)
. (11.2)
В сущности, это координатное равенство для линейного функционала 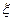 . Но, рассматривая (11.2) как многочлен от
. Но, рассматривая (11.2) как многочлен от 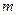 переменных, видим, что это однородный многочлен первой степени, т.е., форма.
переменных, видим, что это однородный многочлен первой степени, т.е., форма.
Лемма 11.1. Если пространство Х конечномерно, то 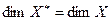 .
.
Доказательство. Это простое следствие теоремы 9.8.
Лемма 11.2. Каждое конечномерное линейное пространство изоморфно своему сопряженному пространству.
Доказательство. Это следствие критерия изоморфности линейных пространств (т.9.8) и предыдущей леммы.
Определение 11.5. Пусть Х – линейное пространство, 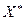 – пространство, ему сопряженное, а
– пространство, ему сопряженное, а 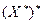 – пространство, сопряженное пространству
– пространство, сопряженное пространству 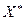 . Тогда пространство
. Тогда пространство 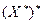 называется вторым (двойным) сопряженным пространством (по отношению к Х).
называется вторым (двойным) сопряженным пространством (по отношению к Х).
Второе сопряженное пространство 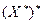 интересно тем, что оно в известной степени
интересно тем, что оно в известной степени
может быть отождествлено с пространством Х. В конечномерном случае эти пространства, очевидно, изоморфны. Но можно доказать существование «естественного» изоморфизма.
Для произвольного пространства Х зададим отображение 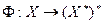 следующим образом:
следующим образом: 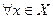 линейный функционал
линейный функционал 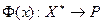 задается равенством
задается равенством
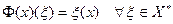 . (11.3)
. (11.3)
Для утверждения о корректности такого определения покажем, что отображение  линейно. Действительно, пусть
линейно. Действительно, пусть 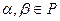 – произвольные элементы поля, а
– произвольные элементы поля, а 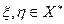 – любые линейные функционалы со значениями в Р. Тогда находим, что
– любые линейные функционалы со значениями в Р. Тогда находим, что
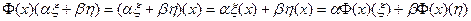 .
.
Теорема 11.1(о естественном изоморфизме).
Для каждого конечномерного линейного пространства отображение 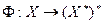 является изоморфизмом.
является изоморфизмом.
Доказательство. Проверим сначала линейность указанного отображения. Вновь зададим произвольные 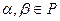 и произвольные
и произвольные 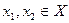 . Надо доказать, что функционалы
. Надо доказать, что функционалы 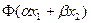 и
и 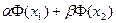 пространства
пространства 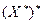 совпадают. Для этого надо доказать, что совпадают их значения на любом
совпадают. Для этого надо доказать, что совпадают их значения на любом 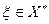 . Вычисляем для
. Вычисляем для 
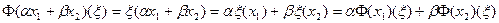 .
.
Как видим, линейность доказана.
Теперь покажем, что 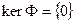 . Это условие равносильно инъективности отображения, а значит и сюръективности. Действительно, если
. Это условие равносильно инъективности отображения, а значит и сюръективности. Действительно, если  , но
, но 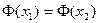 , то
, то  , т.е.,
, т.е., 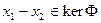 . Значит,
. Значит, 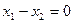 , откуда
, откуда 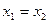 . Получаем противоречие. Значит,
. Получаем противоречие. Значит, 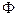 – инъективно. Линейная инъекция отображает линейно независимую систему в линейно независимую. Например, если
– инъективно. Линейная инъекция отображает линейно независимую систему в линейно независимую. Например, если 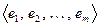 – базис Х, то
– базис Х, то 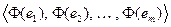 – ЛНЗ. Ибо, если
– ЛНЗ. Ибо, если  , то тогда по линейности отображения
, то тогда по линейности отображения 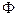 имеем:
имеем: 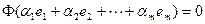 , т.е.,
, т.е., 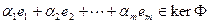 . Значит,
. Значит,
 ,
,
что по критерию ЛНЗ влечет 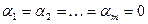 , т.е., система образов линейно независима. Но тогда
, т.е., система образов линейно независима. Но тогда 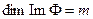 . Учитывая, что
. Учитывая, что 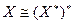 и значит
и значит  , а тогда
, а тогда 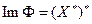 . Таким образом, отображение
. Таким образом, отображение 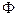 является сюръекцией.
является сюръекцией.
Итак, остается показать, что 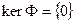 . Пусть
. Пусть 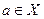 и
и 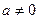 . Дополним его до базиса пространства
. Дополним его до базиса пространства 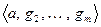 . Определим линейный функционал
. Определим линейный функционал 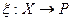 полагая
полагая 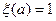 ,
, 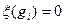 ,
, 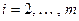 . Продолжим его на все пространство Х по линейности. Таким образом, можно заключить, что для любого ненулевого вектора
. Продолжим его на все пространство Х по линейности. Таким образом, можно заключить, что для любого ненулевого вектора 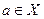 существует линейный функционал
существует линейный функционал 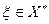 , который на этом векторе принимает ненулевое значение. Поэтому, если для некоторого вектора
, который на этом векторе принимает ненулевое значение. Поэтому, если для некоторого вектора 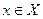 функционал
функционал 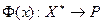 является нулевым (т.е., согласно (11.3)
является нулевым (т.е., согласно (11.3)  для всякого
для всякого 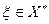 ), то
), то 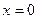 . А это и означает, что
. А это и означает, что 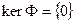 . Теорема доказана.
. Теорема доказана.
Замечание. Доказанная теорема говорит о «естественности» приведенного изоморфизма, свободного от какого-либо произвола, хотя само существование изоморфизма следует из равенства размерностей 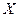 и
и 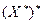 , чем собственно и пользовались.
, чем собственно и пользовались.
Билинейные функционалы
Начнем с определения, где 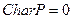 .
.
Определение 11.6. Пусть 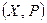 – линейное пространство. Отображение
– линейное пространство. Отображение 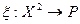 называется билинейным функционалом (или билинейной функцией) на пространстве Х, если при каждом фиксированном значении одного аргумента оно линейно по другому, т.е.,
называется билинейным функционалом (или билинейной функцией) на пространстве Х, если при каждом фиксированном значении одного аргумента оно линейно по другому, т.е.,
1. 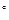
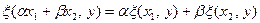 ,
,
2. 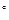
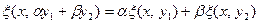 ,
,
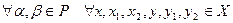 .
.
Пример 11.4. Обычное скалярное произведение в пространствах 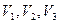 .
.
Пример 11.5. Скалярное произведение в конечномерном евклидовом пространстве..
Пример 11.6. Билинейным функционалом является отображение 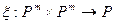 , задаваемое равенством
, задаваемое равенством
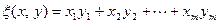 ,
,
где 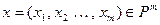 ,
, 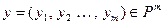 .
.
Пример 11.7. В пространстве 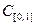 билинейным функционалом будет отображение
билинейным функционалом будет отображение
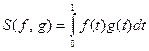
для любых 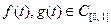 .
.
Определим операции на множестве всех билинейных функционалов на пространстве Х – 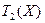 .
.
Определение 11.7. Пусть 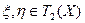 .Тогда их суммой
.Тогда их суммой 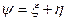 называется отображение
называется отображение 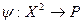 , определяемое соотношением
, определяемое соотношением
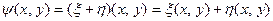 (11.4)
(11.4)
для любых 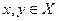 .
.
Определение 11.8. Пусть 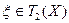 и
и 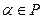 . Тогда произведением элемента
. Тогда произведением элемента 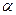 на функционал
на функционал 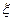 называется отображение
называется отображение  , определяемое соотношением
, определяемое соотношением
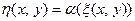 (11.5)
(11.5)
для любых 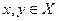 .
.
Лемма 11.3. Отображения, определяемые соотношениями (11.4) и (11.5), являются билинейными функционалами на пространстве Х.
Доказательство. Тривиально.
Лемма 11.4. Множество 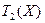 билинейных функционалов на пространстве Х относительно операций сложения и умножения на элементы поля Р образуют линейное пространство над полем Р.
билинейных функционалов на пространстве Х относительно операций сложения и умножения на элементы поля Р образуют линейное пространство над полем Р.
Доказательство. Тривиально и состоит в проверке выполнимости аксиом линейного пространства. Нулем будет нулевой функционал 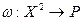 ,
, 
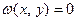 .
.
Определение 11.9. Билинейный функционал 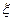 называется симметрическим, если
называется симметрическим, если

для любых 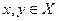 .
.
Определение 11.10. Билинейный функционал 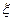 называется кососимметрическим, если
называется кососимметрическим, если

для любых 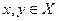 .
.
Множество симметрических билинейных функционалов обозначим через 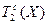 , множество кососимметрических – через
, множество кососимметрических – через 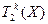 .
.
Лемма 11.5. Множества 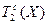 и
и 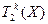 являются подпространствами в
являются подпространствами в 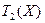 .
.
Доказательство. Проводится с использованием критерия подпространства.
Теорема 11.2. 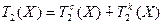 .
.
Доказательство. Действительно, для любого билинейного функционала 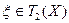 имеем
имеем 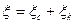 ,
,
где 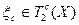 и определяется равенством
и определяется равенством
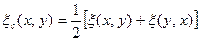 ,
,
а  – равенством
– равенством
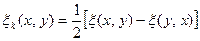 .
.
При этом 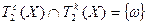 . Теорема доказана.
. Теорема доказана.
Пусть теперь задан билинейный функционал 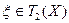 и
и 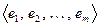 – базис в пространстве Х. Положим
– базис в пространстве Х. Положим 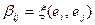 . Составим матрицу
. Составим матрицу 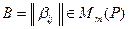 , т.е.,
, т.е.,
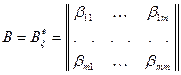 .
.
Такую матрицу назовем матрицей билинейного функционала в базисе 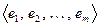 .
.
Элементы 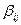 матрицы В называют коэффициентами функционала
матрицы В называют коэффициентами функционала 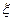 в базисе
в базисе 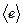 . Если
. Если 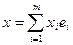 ,
, 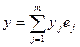 , то в силу билинейности функционала
, то в силу билинейности функционала 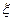 получим
получим

 ,
,
Таким образом,

 . (11.6)
. (11.6)
Определение 11.11. Выражение (11.6) называется билинейной формой билинейного функционала 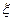 в базисе
в базисе 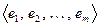 .
.
Следовательно, каждый билинейный функционал в координатной форме в данном базисе представляется билинейной формой. Обратно, всякая билинейная форма задает равенством (11.6) некоторый билинейный функционал. Значит, при фиксированном базисе существует биекция между множеством билинейных функционалов и множеством билинейных форм. Так как билинейная форма однозначно определяется матрицей В, то соотношение (11.6) устанавливает биекцию между билинейными функционалами и их матрицами в фиксированном базисе  . Пусть это будет отображение
. Пусть это будет отображение 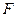 . Тогда легко заметить, что оно линейно, именно:
. Тогда легко заметить, что оно линейно, именно: 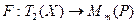 и
и
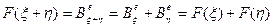 ,
, 
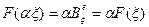 ,
,
для любых 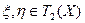 и любого
и любого 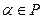 . Таким образом, доказан результат:
. Таким образом, доказан результат:
Теорема 11.3. Отображение 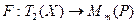 такое, что
такое, что 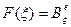 , при фиксированном базисе пространства Х
, при фиксированном базисе пространства Х 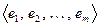 является изоморфизмом между пространством билинейных функционалов
является изоморфизмом между пространством билинейных функционалов 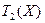 и множеством квадратных матриц порядка
и множеством квадратных матриц порядка 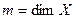 .
.
Замечание. Легко заметить, что симметрическому билинейному функционалу соответствует симметрическая матрица, а кососимметрическому – кососимметрическая в любом базисе.
Равенство (11.6) можно переписать иначе:

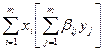 ,
,
Откуда получаем, что

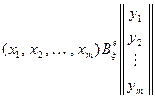 . (11.7)
. (11.7)
Теорема 11.4. Пусть 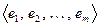 и
и 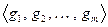 – два базиса линейного пространства Х, и пусть
– два базиса линейного пространства Х, и пусть 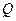 – матрица перехода от базиса
– матрица перехода от базиса 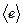 к базису
к базису 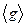 . Тогда для любого билинейного функционала
. Тогда для любого билинейного функционала 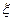 его матрицы в этих базисах связаны соотношением
его матрицы в этих базисах связаны соотношением
 . (11.8)
. (11.8)
Доказательство. Пусть векторы 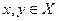 имеют в базисах
имеют в базисах 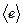 и
и 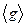 соответственно координаты
соответственно координаты 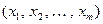 ,
, 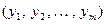 и
и 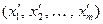 ,
, 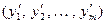 . Тогда, как известно, (см. гл. V)
. Тогда, как известно, (см. гл. V)
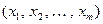
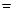
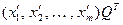 ,
,
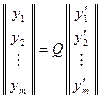 .
.
Поэтому, используя (11.7), находим
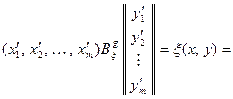
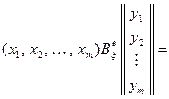
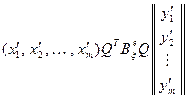 .
.
Сравнивая начало и конец этой выкладки, видим, что получена формула (11.8).
Из формулы (11.8) легко следует, что при переходе от базиса к базису ранг матрицы билинейного функционала не меняется. Таким образом, эта числовая характеристика может быть отнесена к самому функционалу.
Определение 11.12. Рангом билинейного функционала 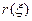 называется ранг его матрицы в каком-либо базисе. Например,
называется ранг его матрицы в каком-либо базисе. Например, 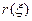
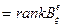 .
.
Определение 11.13. Пусть задан билинейный функционал 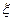 . Тогда положим
. Тогда положим
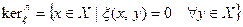 ,
,
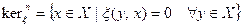
и назовем эти множества соответственно левым и правым ядром функционала 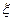 .
.
Лемма 11.6. Левое и правое ядра билинейного функционала являются подпространствами в пространстве Х.
Доказательство. Простое применение критерия подпространства.
Теорема 11.5. Для любого билинейного функционала 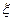 на
на 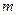 -мерном линейном пространстве Х имеют место равенства
-мерном линейном пространстве Х имеют место равенства
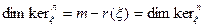 .
.
Доказательство. Рассмотрим правое равенство. Пусть 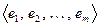 будет каким-либо базисом пространства Х. Легко можно проверить, что
будет каким-либо базисом пространства Х. Легко можно проверить, что
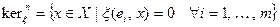 .
.
Тогда для вектора 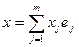 условие принадлежности правому ядру выглядит так:
условие принадлежности правому ядру выглядит так:
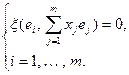
Пользуясь линейностью по второму аргументу, находим
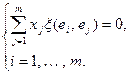
Учитывая описание матрицы билинейного функционала, получаем
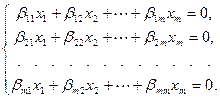
Значит, вектор х принадлежит правому ядру функционала тогда и только тогда, когда его координаты удовлетворяют полученной однородной системе. Матрицей этой системы служит матрица функционала 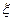 в базисе
в базисе 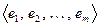 , т.е.,
, т.е., 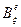 . Поэтому правое ядро можно отождествить (его координатное представление) с общим решением указанной системы. Размерность такого решения есть
. Поэтому правое ядро можно отождествить (его координатное представление) с общим решением указанной системы. Размерность такого решения есть 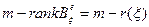 . Что и требовалось. Для левого ядра доказательство проходит по той же схеме. Теорема доказана.
. Что и требовалось. Для левого ядра доказательство проходит по той же схеме. Теорема доказана.
Рассмотрим еще один специальный случай.
Теорема 11.6. Если билинейный функционал 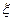 является симметрическим или кососимметрическим, то
является симметрическим или кососимметрическим, то 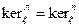 .
.
Доказательство. Пусть 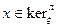 . Это эквивалентно тому, что
. Это эквивалентно тому, что  . Но в зависимости от симметричности или кососимметричности
. Но в зависимости от симметричности или кососимметричности 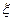 имеем
имеем 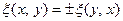 , что в любом случае дает
, что в любом случае дает 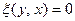 , а это означает принадлежность х правому ядру функционала
, а это означает принадлежность х правому ядру функционала 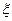 . Равенство размерностей довершает доказательство.
. Равенство размерностей довершает доказательство.
Следствие. Если 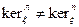 , то функционал
, то функционал 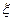 не является ни симметрическим, ни кососимметрическим.
не является ни симметрическим, ни кососимметрическим.
Задача 1. Привести пример билинейного функционала 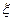 , левое ядро которого не совпадает с правым.
, левое ядро которого не совпадает с правым.
Задача 2. Привести пример билинейного функционала 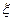 такого, что
такого, что 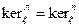 , но не являющегося ни симметрическим, ни кососимметрическим.
, но не являющегося ни симметрическим, ни кососимметрическим.
Квадратичные функции
Определение 11.14. Отображение 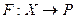 называется квадратичной функцией, если существует такой билинейный функционал
называется квадратичной функцией, если существует такой билинейный функционал 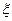 , что
, что
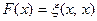 для любого вектора
для любого вектора 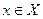 . (11.9)
. (11.9)
Лемма 11.7. Если 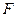 – квадратичная функция, то
– квадратичная функция, то 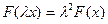
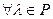 и
и 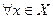 .
.
Доказательство. Очевидное.
Теорема 11.7. Для любой квадратичной функции 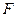 существует единственный симметрический билинейный функционал
существует единственный симметрический билинейный функционал 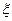 , удовлетворяющий условию (11.9).
, удовлетворяющий условию (11.9).
Доказательство. Единственность. Пусть 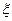 – симметрический билинейный функционал, отвечающий квадратичной функции
– симметрический билинейный функционал, отвечающий квадратичной функции 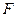 . Тогда в силу (11.9) имеем
. Тогда в силу (11.9) имеем
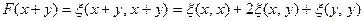 .
.
Отсюда находим, что
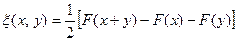 . (11.10)
. (11.10)
Существование. Воспользуемся формулой (11.10) и покажем, что она задает искомый объект. Очевидно, что полученный функционал является симметрическим. Условие (11.9) вытекает из леммы 11.7 для 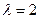 . Действительно,
. Действительно,
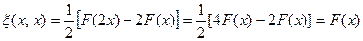 ,
,
где
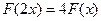 .
.
Остается доказать билинейность. Но так как 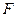 – квадратичная функция, то для нее существует билинейный функционал
– квадратичная функция, то для нее существует билинейный функционал 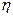 , удовлетворяющий условию (11.9). Следовательно,
, удовлетворяющий условию (11.9). Следовательно,
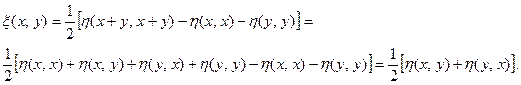
Отсюда вытекает билинейность. Теорема доказана.
Определение 11.15. Билинейный симметрический функционал 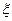 , определяемый квадратичной функцией
, определяемый квадратичной функцией 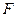 в теореме 11.7, называется функционалом, полярным к квадратичной функции
в теореме 11.7, называется функционалом, полярным к квадратичной функции 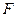 , и обозначается символом
, и обозначается символом 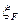 .
.
Итак, формулы (11.9) и (11.10) устанавливают биективное соответствие между квадратичными функциями и симметрическими билинейными функционалами.
Определение 11.16. Матрицей квадратичной функции 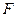 в базисе
в базисе 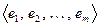 называется матрица
называется матрица  полярного к ней симметрического билинейного функционала.
полярного к ней симметрического билинейного функционала.
Определение 11.17. Рангом квадратичной функции 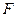 называется ранг билинейного функционала
называется ранг билинейного функционала 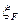 .
.
Если
 ,
,
то для вектора 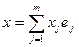 имеем
имеем
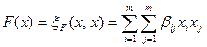 . (11.11)
. (11.11)
Определение 11.18. Выражение, стоящее справа в формуле (11.11) называется квадратичной формой от переменных 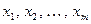 и обозначается
и обозначается 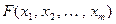 .
.
Квадратичная форма – это однородный многочлен второй степени. Ее матрицей является симметрическая матрица  , а рангом формы называется ранг ее матрицы. Таким образом, квадратичная форма есть координатное представление квадратичной функции в некотором базисе. Квадратичную функцию в матричной форме можно записать и так
, а рангом формы называется ранг ее матрицы. Таким образом, квадратичная форма есть координатное представление квадратичной функции в некотором базисе. Квадратичную функцию в матричной форме можно записать и так

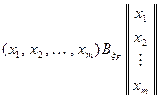 .
.
При переходе к новому базису сохраняется формула (11.8).
Вещественные квадратичные формы
Теперь положим поле  , т.е., полю вещественных чисел. Будем рассматривать евклидово пространство
, т.е., полю вещественных чисел. Будем рассматривать евклидово пространство 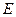 и
и 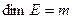 с заданным в нем ортонормированным базисом
с заданным в нем ортонормированным базисом 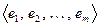 . В таком базисе, как известно, скалярное произведение выглядит, как сумма попарных произведение одноименных координат векторов. Как и ранее, квадратичную функцию задаем в виде квадратичной формы
. В таком базисе, как известно, скалярное произведение выглядит, как сумма попарных произведение одноименных координат векторов. Как и ранее, квадратичную функцию задаем в виде квадратичной формы
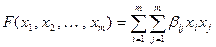 ,
,
где 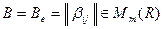 – симметрическая матрица формы. Саму форму, учитывая вид скалярного произведения и вид вектора
– симметрическая матрица формы. Саму форму, учитывая вид скалярного произведения и вид вектора 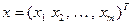 можно представить следующим образом:
можно представить следующим образом:
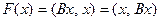 .
.
Переход к новому базису запишем как линейное невырожденное преобразование формы.
Определение 11.19. Линейным невырожденным преобразованием (ЛНП) квадратичной формы 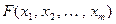 называется преобразование вида:
называется преобразование вида:
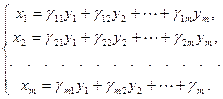
Здесь матрица  , т.е., невырожденная.
, т.е., невырожденная.
Такое преобразование отвечает переходу к новому базису 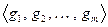 с матрицей перехода
с матрицей перехода  . Именно, прежние переменные описываются через новые посредством формулы
. Именно, прежние переменные описываются через новые посредством формулы
 ,
,
где 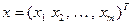 ,
,  – координатные столбцы вектора
– координатные столбцы вектора 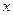 в старом и новом базисе. В этой записи
в старом и новом базисе. В этой записи 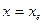 , а
, а 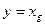 .
.
Линейное невырожденное преобразование не меняет ранга формы, ибо после преобразования матрица формы приобретает вид, следующий из формулы
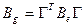 .
.
Лемма 11.8. Применение двух последовательных ЛНП к форме можно заменить одним преобразованием, матрица которого есть произведение матриц последовательных преобразований.
Доказательство. Пусть к форме 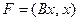 применили два преобразования
применили два преобразования 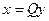 и
и 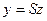 . Тогда имеем
. Тогда имеем
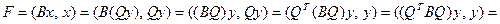
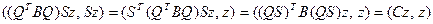 ,
,
где 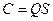 .
.
Определение 11.20. Вещественная квадратичная форма имеет канонический вид, если ее матрица диагональна.
Таким образом, в каноническом виде отсутствуют попарные произведения переменных, и форма приобретает следующее представление:
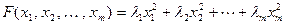 . (11.12)
. (11.12)
Определение 11.21. Канонический вид вещественной квадратичной формы называется нормальным видом, если коэффициенты при квадратах переменных равны 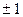 или 0.
или 0.
Лемма 11.9. Вещественную квадратичную форму, записанную в каноническом виде (11.12), можно привести к нормальному виду с помощью стандартного ЛНП.
Доказательство. Не ограничивая общности рассуждений можно считать, что первые 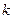 коэффициентов в каноническом виде положительны, следующие
коэффициентов в каноническом виде положительны, следующие 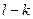 – отрицательны и, наконец, последние
– отрицательны и, наконец, последние 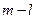 равны нулю. Если это не так, то можно провести перенумерацию переменных, что, очевидно, является невырожденным преобразованием. Тогда, достаточно применить преобразование
равны нулю. Если это не так, то можно провести перенумерацию переменных, что, очевидно, является невырожденным преобразованием. Тогда, достаточно применить преобразование

Ясно, что матрица преобразования невырожденная, а форма приобретает нормальный вид:
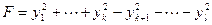 .
.
Теорема 11.8 (приведение вещественной квадратичной формы к главным осям). Каждую вещественную квадратичную форму можно привести к каноническому виду линейным невырожденным преобразованием с ортогональной матрицей.
Доказательство. Из главы Х (лемма 10.10) известно, что каждая симметрическая матрица ортогонально подобна вещественной диагональной матрице, т.е., если  – симметрическая, то существует ортогональная матрица
– симметрическая, то существует ортогональная матрица 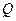 такая, что
такая, что  , где
, где 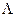 – диагональная матрица. Применим к форме
– диагональная матрица. Применим к форме 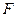 ЛНП
ЛНП 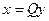 . Тогда получим
. Тогда получим
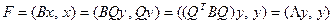 .
.
Ввиду диагональности матрицы 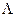 форма приобретает канонический вид. Теорема доказана.
форма приобретает канонический вид. Теорема доказана.
Применение этой теоремы к теории кривых и поверхностей второго порядка обусловило ее название.
Пример 11.8. Привести квадратичную форму

к главным осям и выписать соответствующее ортогональное преобразование переменных.
Учитывая тот факт, что преобразование подобия в данном случае приводит к матрице 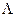 , на главной диагонали которой располагаются собственные значения симметрической матрицы (оператора), требуется найти эти собственные значения. Составим характеристическую матрицу для данной матрицы В и найдем ее определитель. Итак,
, на главной диагонали которой располагаются собственные значения симметрической матрицы (оператора), требуется найти эти собственные значения. Составим характеристическую матрицу для данной матрицы В и найдем ее определитель. Итак,
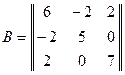 ,
,
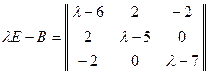 ,
,
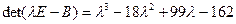 .
.
Корни характеристического многочлена, вычисленные по схеме Горнера таковы: 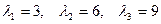 . Таким образом, канонический вид уже определен. Это будет
. Таким образом, канонический вид уже определен. Это будет
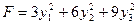 ,
,
т.е., матрица 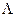 имеет вид
имеет вид
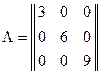 .
.
Займемся нахождением самого ортогонального преобразования. Можно считать, что матрица В записана в единичном базисе, который с введенным скалярным умножением является ортонормированным. Поэтому требуется найти ортонормированный собственный базис симметрической матрицы (оператора), переход к которому задается преобразованием с ортогональной матрицей (см. л. 10.6). Для этого придется найти собственные подпространства матрицы В. Имеем для 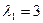 :
:
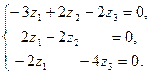
Получаем общее решение 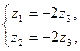
Откуда собственное подпространство описывается через фундаментальную систему решений 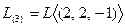 . Теперь для
. Теперь для 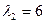 имеем:
имеем:

Вновь выписываем общее решение
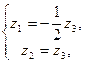
и теперь 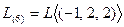 . Наконец, для
. Наконец, для 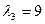 находим
находим
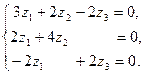
Общее решение: 
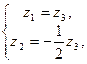
и получаем собственное подпространство 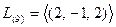 .
.
Из базисных векторов собственных подпространств строим ортогональный базис. При этом ортогонализация не нужна, ибо собственные векторы относятся к попарно различным собственным значениям. Их лишь остается пронормировать. Таким образом, получим ОНСБ: 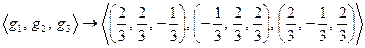 . Матрица перехода
. Матрица перехода 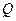 от единичного базиса
от единичного базиса 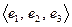 к базису
к базису 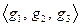 будет, очевидно, ортогональной и записывается тривиально:
будет, очевидно, ортогональной и записывается тривиально:
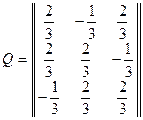 .
.
Отсюда легко запишем ортогональное ЛНП:

Рассмотрим еще один результат, имеющий конструктивный характер и приводящий квадратичную форму к нормальному виду.
Теорема 11.9 (метод Лагранжа).
Каждую вещественную квадратичную форму можно привести к нормальному виду линейным невырожденным преобразованием переменных.
Доказательство. Пусть задана форма от 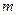 переменных
переменных
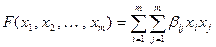 .
.
Проведем доказательство методом математической индукции по числу переменных 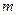 . Если
. Если 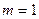 , то форма имеет вид
, то форма имеет вид  , т.е., имеет канонический вид, который приводится к нормальному при помощи леммы 11.9. Пусть теперь теорема справедлива для всех
, т.е., имеет канонический вид, который приводится к нормальному при помощи леммы 11.9. Пусть теперь теорема справедлива для всех  . Докажем теорему для значения
. Докажем теорему для значения 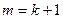 . Доказательство разобьем на два случая. В первом будем считать, что в записи формы есть квадраты переменных. Таким образом, существует номер
. Доказательство разобьем на два случая. В первом будем считать, что в записи формы есть квадраты переменных. Таким образом, существует номер 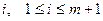 , что
, что 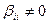 . Для простоты рассуждений
. Для простоты рассуждений
считаем, что 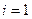 . Тогда построим разность
. Тогда построим разность
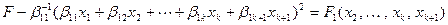 .
.
Выражение в левой части равенства представляет собой разность двух квадратичных форм от  переменной и, следовательно, является тоже квадратичной формой. Но зависит эта форма лишь от
переменной и, следовательно, является тоже квадратичной формой. Но зависит эта форма лишь от 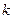 переменных, ибо вычитаемая форма имеет с исходной одинаковые слагаемые, содержащие переменную
переменных, ибо вычитаемая форма имеет с исходной одинаковые слагаемые, содержащие переменную  . Применим преобразование вида
. Применим преобразование вида
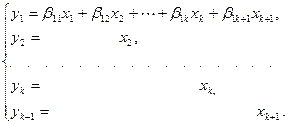
Тогда исходная форма перепишется в виде
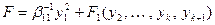 .
.
Форма 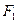 зависит лишь от
зависит лишь от 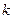 переменных, следовательно, по индуктивному предположению может быть приведена к каноническому виду некоторым ЛНП ее
переменных, следовательно, по индуктивному предположению может быть приведена к каноническому виду некоторым ЛНП ее 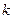 переменных. Дополняя это преобразование переобозначением
переменных. Дополняя это преобразование переобозначением 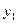 , получаем ЛНП уже
, получаем ЛНП уже  переменной, что дает, например,
переменной, что дает, например,
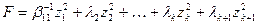 .
.
Приведение к нормальному виду теперь осуществляется по лемме 11.9. Здесь надо заметить, что первое преобразование было не прямым. В силу невырожденности его можно обратить и выписать соответствующую матрицу преобразования, которую использовать для получения результирующего преобразования. Именно
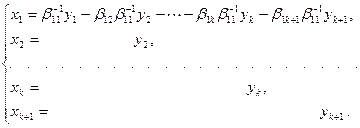
Если теперь обозначить через 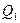 матрицу этого преобразования, через
матрицу этого преобразования, через 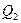 – матрицу расширенного преобразования, приводящего
– матрицу расширенного преобразования, приводящего 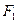 к каноническому виду и, наконец, через
к каноническому виду и, наконец, через 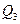 – матрицу, приводящую канонический вид к нормальному (лемма 11.9), то в итоге получим преобразование
– матрицу, приводящую канонический вид к нормальному (лемма 11.9), то в итоге получим преобразование  , выражающее форму
, выражающее форму 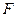 через переменные
через переменные 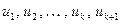 , представленную в нормальном виде.
, представленную в нормальном виде.
Вторая часть доказательства предполагает, что в записи формы отсутствуют квадраты переменных, т.е.,  . Считая форму отличной от нулевой, полагаем, что существует коэффициент
. Считая форму отличной от нулевой, полагаем, что существует коэффициент 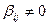 , но тогда в записи формы присутствует слагаемое
, но тогда в записи формы присутствует слагаемое 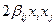 . Не ограничивая общности рассуждений, положим
. Не ограничивая общности рассуждений, положим 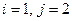 . Выполним вспомогательное ЛНП следующего вида:
. Выполним вспомогательное ЛНП следующего вида:
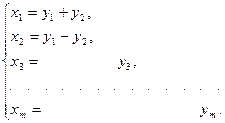
Матрица этого преобразования имеет следующий вид:
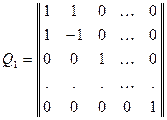 ,
,
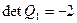 , поэтому преобразование невырожденное. Но оно позволяет получить в записи формы два квадрата переменных, именно:
, поэтому преобразование невырожденное. Но оно позволяет получить в записи формы два квадрата переменных, именно: 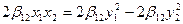 . Эти слагаемые не могут сократиться за счет других слагаемых, ибо эти другие слагаемые содержат и другие пары переменных. Теперь приходим к ситуации, которая описана в первой части доказательства. Значит, если первая часть с помощью ЛНП
. Эти слагаемые не могут сократиться за счет других слагаемых, ибо эти другие слагаемые содержат и другие пары переменных. Теперь приходим к ситуации, которая описана в первой части доказательства. Значит, если первая часть с помощью ЛНП 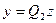 приводит преобразованную форму к нормальному виду, то исходную форму можно преобразовать с помощью ЛНП
приводит преобразованную форму к нормальному виду, то исходную форму можно преобразовать с помощью ЛНП 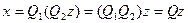 . Теорема доказана.
. Теорема доказана.
Как уже говорилось, эта теорема носит конструктивный характер, т.е., используя доказательство можно реально приходить к нормальному виду формы и выписывать соответствующее ЛНП.
Пример 11.9. Привести квадратичную форму

к нормальному виду методом Лагранжа и записать результирующее ЛНП.
По внешнему виду формы ясно, что придется выполнять вспомогательное ЛНП, производящее квадраты переменных. Получаем
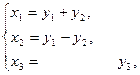
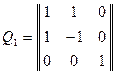 .
.
Тогда
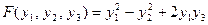 .
.
Составим разность
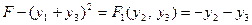 .
.
Сделаем линейную замену переменных
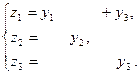
Получим
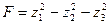 .
.
В данном случае сразу получается форма нормального вида. Ей отвечает матрица
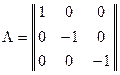 .
.
Запишем результирующее преобразование. Для этого сначала найдем обратное ко второму.
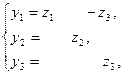
 .
.
Вычислим результирующую матрицу, перемножая матрицы последовательных преобразовании.
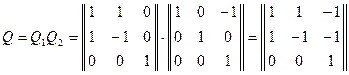 .
.
Восстановим по матрице само преобразование. Имеем


Можно сделать проверку. Запишем матрицу исходного вида формы
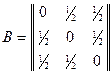 .
.
Теперь вычислим произведение 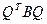 . Находим
. Находим
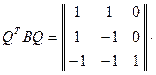
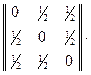
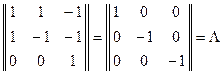 .
.
Это подтверждает правильность решения задачи.
Приведение квадратичной формы к нормальному виду заведомо неоднозначно и может быть выполнено разными подходами. Тем не менее, имеются инварианты, сохраняющие свое значение при любых ЛНП.
Теорема 11.10 (закон инерции вещественных квадратичных форм).
Количество положительных и количество отрицательных слагаемых в нормальном виде вещественной квадратичной формы не зависит от того линейного невырожденного преобразования, которым она к нормальному виду приведена.
Доказательство. Предположим противное. Пусть двумя ЛНП форма от  переменных
переменных
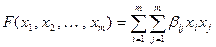
приведена к двум различным нормальным видам:
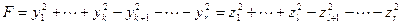 . (11.13)
. (11.13)
Здесь  означает ранг формы, который естественно не меняется от применения ЛНП. Очевидно, что
означает ранг формы, который естественно не меняется от применения ЛНП. Очевидно, что 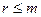 . Пусть первый нормальный вид получен при помощи ЛНП, обратного к следующему:
. Пусть первый нормальный вид получен при помощи ЛНП, обратного к следующему:
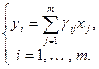 (11.14)
(11.14)
Обратное преобразование существует ввиду невырожденности матрицы исходного преобразования. При этом матрица 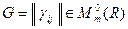 . Второй нормальный вид получен ЛНП, обратным к такому:
. Второй нормальный вид получен ЛНП, обратным к такому:
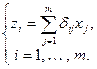 (11.15)
(11.15)
Здесь матрица 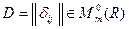 . Предположим, что
. Предположим, что 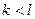 и составим следующую систему линейных алгебраических уравнений от переменных
и составим следующую систему линейных алгебраических уравнений от переменных 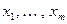 , используя выражения (11.14) и (11.15):
, используя выражения (11.14) и (11.15):
 (11.16)
(11.16)
Система (11.16) содержит меньше уравнений, чем неизвестных. Действительно,
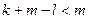 .
.
Поэтому такая система имеет нетривиальное решение 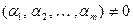 . Подставим это решение в равенство (11.13), предварительно заменив переменные на выражения, зависящие от
. Подставим это решение в равенство (11.13), предварительно заменив переменные на выражения, зависящие от 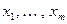 по формулам (11.14) и (11.15) и описав соответствующую подстановку через
по формулам (11.14) и (11.15) и описав соответствующую подстановку через 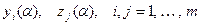 . Тогда получим
. Тогда получим
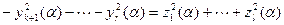 .
.
Из этого равенства становится ясным, что 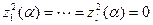 . И, значит,
. И, значит, 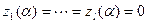 Рассмотрим теперь новую систему линейных алгебраических уравнений
Рассмотрим теперь новую систему линейных алгебраических уравнений
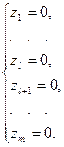
Эта система относительно 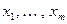 имеет матрицу коэффициентов при неизвестных
имеет матрицу коэффициентов при неизвестных 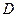 .
.
В силу ее невырожденности по правилу Крамера такая система имеет единственное частное решение, и это решение нулевое, ибо система однородная. Но сказанное противоречит тому, что решением системы является ненулевой набор 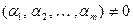 .
.
Возникающее противоречие доказывает, что предположение о том, что 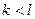 неверно. Аналогично можно доказать, что и предложение
неверно. Аналогично можно доказать, что и предложение 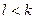 тоже неверно. Поэтому
тоже неверно. Поэтому 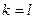 . Теорема доказана.
. Теорема доказана.
Эта теорема позволяет ввести в обращение следующие термины.
Определение 11.22. Количество положительных квадратов в нормальном виде вещественной квадратичной формы называется ее положительным индексом инерции (р), количество отрицательных – отрицательным индексом инерции (q), а разность первого и второго – сигнатурой квадратичной формы (s).
Пример 11.10. В предыдущем примере 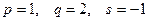 .
.
Определение 11.23. Две вещественные квадратичные формы от 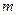 переменных называются аффинно эквивалентными, если одна из них может быть преобразована в другую линейным невырожденным преобразованием.
переменных называются аффинно эквивалентными, если одна из них может быть преобразована в другую линейным невырожденным преобразованием.
Лемма 11.10. Бинарное отношение аффинной эквивалентности на множестве всех вещественных квадратичных форм от 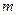 переменных есть отношение эквивалентности.
переменных есть отношение эквивалентности.
Доказательство. Тривиальное.
Теорема 11.11 (критерий аффинной эквивалентности форм).
Две вещественные квадратичные формы от 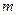 переменных аффинно эквивалентны тогда и только тогда, когда совпадают их ранги и сигнатуры.
переменных аффинно эквивалентны тогда и только тогда, когда совпадают их ранги и сигнатуры.
Доказательство. Необходимость. Если формы аффинно эквивалентны, то одна из них переводится в другую некоторым ЛНП с матрицей 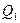 , а вторая при этом может быть преобразована к некоторому нормальному виду с помощью ЛНП с матрицей
, а вторая при этом может быть преобразована к некоторому нормальному виду с помощью ЛНП с матрицей 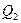 . Тогда первая форма преобразуется к тому же нормальному виду с помощью ЛНП с матрицей
. Тогда первая форма преобразуется к тому же нормальному виду с помощью ЛНП с матрицей  .
.
Достаточность. Если у двух форм одинаковые ранги и сигнатуры, то они обладают одинаковыми нормальными видами, с точностью до нумерации переменных. Поэтому, если первая преобразуется к нормальному виду ЛНП с матрицей 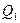 , а вторая к тому же виду с матрицей
, а вторая к тому же виду с матрицей 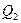 , то первая может быть преобразована во вторую с помощью ЛНП с матрицей
, то первая может быть преобразована во вторую с помощью ЛНП с матрицей  . Теорема доказана.
. Теорема доказана.
Замечание. Пара чисел  и
и 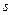 в формулировке теоремы может быть заменена на любую пару из множества
в формулировке теоремы может быть заменена на любую пару из множества 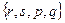 .
.
Задача. Вычислить количество классов аффинной эквивалентности для форм от 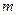 переменных.
переменных.
Определение 11.24. Вещественная квадратичная форма называется положительно определенной, если на любом ненулевом наборе значений переменных принимает строго положительные значения.
Теорема 11.12 (первый критерий положительной определенности формы).
Вещественная квадратичная форма от
