Оценка параметров линейной регрессии
Установим некоторые свойства параметров (8.2.8) и (8.2.9), полученных методом наименьших квадратов:
A) линейная зависимость 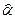 и
и 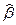 от наблюдаемых значений показателя
от наблюдаемых значений показателя 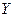 ;
;
B) 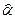 и
и 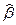 являются несмещенными оценками истинных параметров
являются несмещенными оценками истинных параметров 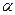 и
и 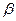 (в соотношении
(в соотношении 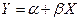 );
);
C) 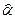 и
и 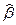 являются наилучшими линейными несмещенными оценками
являются наилучшими линейными несмещенными оценками 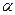 и
и 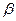 .
.
Эти свойства показывают состоятельность найденных оценок и не требуют дополнительных комментариев. Заметим только, что параметры 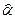 и
и 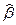 можно рассматривать как случайные величины, считая наблюдаемые значения
можно рассматривать как случайные величины, считая наблюдаемые значения 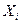 ,
, 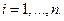 , фиксированными, т.е. одинаковыми во всех выборках. В этом случае величина
, фиксированными, т.е. одинаковыми во всех выборках. В этом случае величина 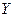 будет меняться от выборки к выборке в силу различий в значениях переменной
будет меняться от выборки к выборке в силу различий в значениях переменной 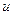 (см. (8.2.3) ), которые подчиняются вероятностному распределению. Применяя формулы (8.2.8) и (8.2.9) для
(см. (8.2.3) ), которые подчиняются вероятностному распределению. Применяя формулы (8.2.8) и (8.2.9) для 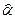 и
и 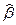 к каждому множеству выборочных наблюдений
к каждому множеству выборочных наблюдений 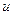 , образуем последовательность оценок
, образуем последовательность оценок 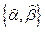 . Используя распределения величин
. Используя распределения величин 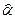 и
и 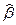 , можно вычислить средние значения
, можно вычислить средние значения 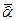 ,
, 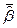 и дисперсии, где
и дисперсии, где 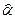 и
и 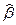 являются несмещенными оценками параметров
являются несмещенными оценками параметров 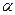 и
и 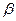 , если
, если 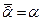 ,
, 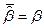 .
.
Относительно случайной величины 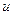 в (8.2.3) будем предполагать, что
в (8.2.3) будем предполагать, что
a) среднее значение случайной величины 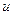 равно нулю;
равно нулю;
b) дисперсия случайной величины 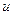 постоянна и не зависит от
постоянна и не зависит от 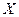 ;
;
c) ковариация различных значений 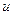 равна нулю.
равна нулю.
Условие 1) говорит о том, что для фиксированного значения X возможные значения 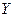 группируются вокруг центрального значения
группируются вокруг центрального значения 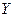 , каким является ее среднее значение (см. Пример 8.2); условие 2) говорит об одинаковых распределениях вероятностей величины
, каким является ее среднее значение (см. Пример 8.2); условие 2) говорит об одинаковых распределениях вероятностей величины 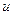 для разных значений
для разных значений 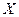 , например, дисперсия
, например, дисперсия 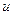 не возрастает с ростом значений
не возрастает с ростом значений 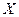 ; условие 3) означает, что любое значение
; условие 3) означает, что любое значение 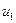 , положительное или отрицательное, никаким образом не влияет на значения
, положительное или отрицательное, никаким образом не влияет на значения 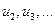 и в этом случае точки выборки более или менее тесно группируются вокруг прямой линии
и в этом случае точки выборки более или менее тесно группируются вокруг прямой линии 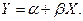
Проверим выполнение свойства A). Перепишем соотношение (8.2.8) в виде:
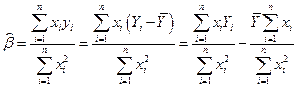 .
.
Покажем, что 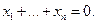 Действительно,
Действительно,
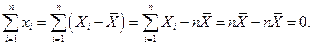
Поэтому
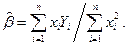
Обозначим
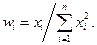
Тогда можно написать линейную зависимость 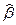 от
от 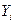 :
:
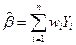 . (8.3.1)
. (8.3.1)
Непосредственно убеждаемся, что
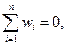
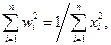
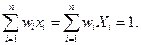
Используя (8.3.1) , из (8.2.9) получаем:
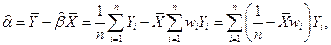
т.е. 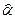 действительно является линейной функцией от
действительно является линейной функцией от 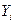 .
.
Проверим выполнение свойства B). Из (8.2.3) находим
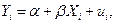
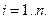
Используя формулу (8.3.1) и свойства 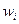 , получим
, получим
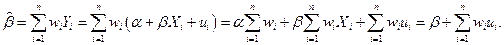
Вычислим среднее значение 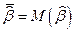 :
:
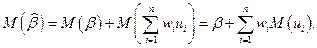
Согласно условию a) 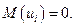 Поэтому
Поэтому 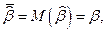 т.е.
т.е. 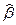 есть несмещенная оценка параметра
есть несмещенная оценка параметра 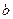 . Параметр
. Параметр 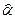 можно представить следующим образом:
можно представить следующим образом:
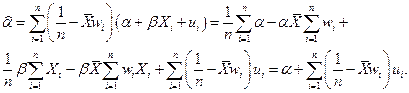
Применяя операцию получения математического ожидания и пользуясь условием a), находим: 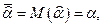 т.е.
т.е. 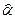 также является несмещенной оценкой параметра
также является несмещенной оценкой параметра 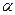 .
.
Докажем свойство С. Составим оптимизационную задачу для получения наилучших линейных несмещенных оценок и покажем, что оценки наименьших квадратов совпадают с решением этой задачи. Покажем это для параметра 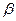 , (для
, (для 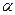 аналогично).
аналогично).
Из всех несмещенных оценок вида
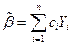
параметра 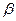 наилучшей будет та, у которой дисперсия
наилучшей будет та, у которой дисперсия 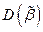 минимальна. Пользуясь выборочными данными, запишем:
минимальна. Пользуясь выборочными данными, запишем:
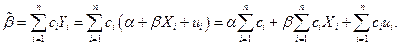
Вычислим математическое ожидание:
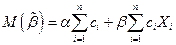
(здесь использовано условие a)). Следовательно, 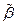 будет несмещенной оценкой
будет несмещенной оценкой 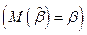 тогда и только тогда, когда
тогда и только тогда, когда
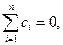
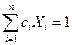 . (8.3.2)
. (8.3.2)
При выполнении этих условий вычислим дисперсию 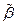 :
:
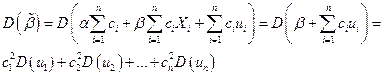
(здесь имеется в виду независимость случайных величин 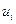 по свойству c)). Используя свойство b), имеем
по свойству c)). Используя свойство b), имеем
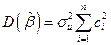 ,
,
где 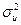 - среднеквадратическое отклонение случайных величин
- среднеквадратическое отклонение случайных величин 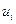 , одинаковое для всех
, одинаковое для всех 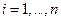 . Составим оптимизационную задачу:
. Составим оптимизационную задачу:
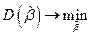
Так как множество несмещенных оценок 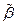 сопряжено с множеством весов
сопряжено с множеством весов 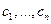 , удовлетворяющих условиям (8.3.2) , и с учетом того, что
, удовлетворяющих условиям (8.3.2) , и с учетом того, что
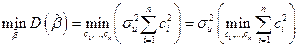
задача эквивалентным образом запишется в виде
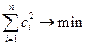
при ограничениях
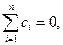
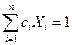
Для решения этой задачи введем множители 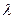 и
и 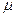 и составим функцию Лагранжа
и составим функцию Лагранжа
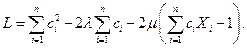
Необходимые условия оптимальности (см. (2.3.9)), состоящие из условий стационарности и допустимости, после некоторых преобразований имеют вид:
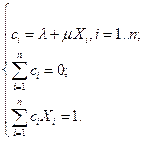
Просуммировав первое уравнение по 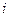 , получим равенство
, получим равенство 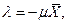 которое подставим в первое уравнение:
которое подставим в первое уравнение:
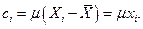
Умножив это уравнение на 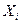 , просуммировав по
, просуммировав по 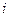 и воспользовавшись третьим уравнением, получим
и воспользовавшись третьим уравнением, получим
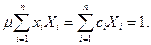
Таким образом,
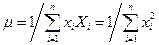
и, следовательно,
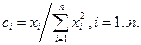
Тем самым показано, что веса 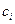 равны весам
равны весам 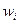 в оценке
в оценке 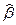 , полученной методом наименьших квадратов (см. (8.3.1)), и поэтому
, полученной методом наименьших квадратов (см. (8.3.1)), и поэтому 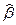 будет наилучшей линейной несмещенной оценкой параметра
будет наилучшей линейной несмещенной оценкой параметра 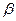 . Аналогично доказывается этот факт для оценки
. Аналогично доказывается этот факт для оценки 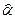 .
.
Таким образом, если
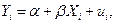
где ошибки 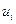 удовлетворяют условиям a), b), c), а
удовлетворяют условиям a), b), c), а 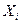 - фиксированные константы, то оценки наименьших квадратов
- фиксированные константы, то оценки наименьших квадратов
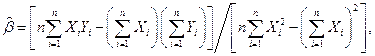
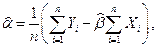
являются наилучшими линейными несмещенными оценками параметров 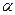 и
и 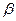 , а их дисперсии равны:
, а их дисперсии равны:
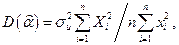 (8.3.3)
(8.3.3)
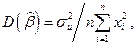 (8.3.4)
(8.3.4)
где 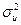 - одинаковое для всех
- одинаковое для всех 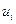 среднеквадратическое отклонение.
среднеквадратическое отклонение.
Заметим, что при более детальном анализе оценок 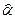 и
и 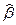 исследуют еще и их «максимальное правдоподобие». Однако изучение этого свойства требует введения ряда новых достаточно сложных понятий. То же самое относится и к обобщению рассмотренного регрессионного анализа в двух направлениях: во-первых, нелинейного регрессионного анализа - когда корреляционная зависимость между
исследуют еще и их «максимальное правдоподобие». Однако изучение этого свойства требует введения ряда новых достаточно сложных понятий. То же самое относится и к обобщению рассмотренного регрессионного анализа в двух направлениях: во-первых, нелинейного регрессионного анализа - когда корреляционная зависимость между 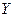 и
и 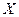 нелинейна; во-вторых, многомерного регрессионного анализа - когда
нелинейна; во-вторых, многомерного регрессионного анализа - когда 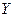 зависит от многих объясняющих переменных
зависит от многих объясняющих переменных 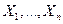 .
.
Дата добавления: 2019-07-26; просмотров: 135;
