Гамильтонова реализация графической последовательности
В этом параграфе будет показано, как с помощью гроцедуры построить реализацию графической последо-тельности, обладающую гамильтоновой цепью или гамильтоновым циклом, если такие реализации существуют.
В формулировке следующего утверждения используется обозначение S(v), введенное в § 46.
Теорема 48.1 (В. Чангфейзен, 1978 г.). Если существует реализация правильной п-последователъности d,имеющая гамильтонову цепь с началом в вершине степени di , то к такой реализации приведет l-процедура, на первом шаге которой ведущей является вершина степени di, а на каждом из последующих — вершина с минимальной положительной меткой из множества S(v), где v — вершина, ведущая на предыдущем шаге.
Доказательство этой теоремы требует перебора возможных вариантов и потому громоздко; здесь оно опускается.
Перейдем к построению гамильтоновой реализации. Оно основано на следующей теореме.
Теорема 48.2 (В. Чангфейзен, 1978 г.). Для того чтобы правильная п-последователъность d имела реализацию в виде гамильтонова графа, необходимо и достаточно выполнение следующих двух условий.
1)  di > 1, 1 = 1, п;
di > 1, 1 = 1, п;
2) существует реализация последовательности d, имеющая гамильтонову цепь с началом в вершине степени di.
Необходимость условия теоремы тривиальна, докажем достаточность. Пусть G — реализация последовательности d, имеющая гамильтонову цепь (v1 ,v2 ,...,vn) с началом в вершине v1 степени d1. Если v1vn € EG, то (v1 ,v2 ,...,vn ,v1) — гамильтонов цикл.
Пусть v1vn ¢ EG. Тогда вершина vn смежна с какой-либо вершиной vi , где 1< i <n — 1. Рассмотрим вершину vi+1 . Если v1vi+1 € EG, то
(v1 ,v2 ,... ,vi ,vn ,vn-1 ,.., vi+1 ,v1)
— гамильтонов цикл. Пусть теперь vivi+1 ¢ EG. Поскольку вершина vi смежна как с vi+1 , так и с vn, а вершина v1 не смежна ни с vi+1 , ни с vn , хотя deg v1 ≥
≥ deg vi , то существует такая вершина vk, что k ≠ 2, vivk € EG, vivk ¢ EG. Но тогда граф G допускает переключение s = (vivk , vi+1vi). Граф sG имеет гамильтонов цикл
 |
(v1 ,v2 ,... ,vi ,vn ,vn-1 ,.., vi+1 ,v1)
(рис. 48.1).
На рис. 48.2 показана процедура построения гамильтоновой реализации последовательности (З2, 24). Получен граф G с гамильтоповой цепью (1, 3, 2, 5, 6, 4); (1, 3, 2, 5, 6, 4, 1)— гамильтонов цикл.
Расщепляемые графы
Некоторые свойства графов полностью определяются стененными последовательностями, т. е. либо присущи всем реализациям степенной последовательности, либо и одной из них. Одно из таких свойств — расщепляемость.
Граф G называется расщепляемым, если существует разбиение множества его вершин на клику и независимое множество, т. е. такое разбиение
AUB = VG, (1)
что порожденный подграф G(A) является полным, G(B)—пустым. Это разбиение называется полярным. Множество А называется верхней долей графа G, а В — нижней; одна из этих долей может быть пустой.
Как подтверждает простая проверка, все графы порядка п ≥ 3 расщепляемы, но уже среди четырехвершинных графов есть и расщепляемые и не расщепляемые.
Для правильной графической последовательности d преведем параметр m(d), положив
т(d) = max {i: di ≥ i—l}.
Например, m(d)=3 для d = (42, 22, I2).
Теорема 49.1 (П. Хаммер, Б. Симеоне, 1981 г.). Пустъ d — правильная графическая п-последовательностъ, G — ее произвольная реализация. Граф G расщепляем тогда и только тогда, когда верно равенство
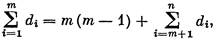 |
где m = m(d).
Пусть G — расщепляемый граф. Среди всех полярных разбиений множества VG выберем разбиение (1) с максимальным числом вершин в верхней доле. Очевидно, что если а €А, b € В и IАI = k, то deg а ≥ k — 1, deg b < k. Следовательно, m = к. Поскольку G (А) = Кт, G(В) = Оп-m , то верно равенство (2).
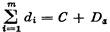 |
Обратно, пусть для некоторого графа G VG = {1, 2, ... .., п}, deg i = di. Положим A = {1, 2, ..., т}, В = {m + l, ..., п) и сумму степеней вершин из А разобьем на две части:
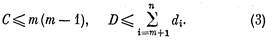 |
где С — вклад, вносимый в эту сумму ребрами вида а1а2 , аi € А, а D — тот вклад, который вносят ребра вида ab, а € А, b € В. Очевидно, что верны неравенства
Равенство (2) верно только тогда, когда оба неравенства (3) являются равенствами. Но это и означает, что G(A) = Кт , G(B) = Оп-т.
Очевидно
Следствие 49.2. Если одна из реализаций графической последовательности расщепляема, то и все ее реализации расщепляемы.
Графическая последовательность называется расщепляемой, если она имеет расщепляемую реализацию.
При доказательстве достаточности выполнения условия (2) для расщепляемости графической последовательности d не были использованы ни смысл параметра m(d), ни то, что последовательность d не возрастает. Поэтому верно
Утверждение 49.3. Для расщепляемости графической п-последователъности d необходимо и достаточно, чтобы для какого-либо m, l≤m≤n, выполнялось равенство (2).
Расщепляемые графы составляют важный и содержательный класс графов. В частности, он включает в себя все пороговые графы, рассматриваемые в следующем параграфе. Некоторые задачи, сложные в общей ситуации (например, задача построения наибольшего независимого множества), становятся тривиальными в классе расщепляемых графов. Другие задачи для этого класса графов столь же сложны, как и для произвольных графов. Известно, например, что проблема изоморфизма произвольных графов просто сводится к аналогичной проблеме для расщепляемых графов (см. [18]).
Характеризация расщепляемых графов в терминах запрещенных порожденных подграфов приведена в § 62.
Пороговые графы
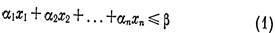 |
Среди расщепляемых графов важный класс составляют пороговые графы. Вершины произвольного графа G порядка п занумеруем числами 1, 2, ..., п, т. е. положим VG = 1, 2, ..., п). Как и в§ 28, обозначим через ƒG множество, элементами которого служат все независимые подмножества вершин графа G и пустое множество. Если существуют такие неотрицательные вещественные числа ά1, ά2, … , άn что множество всех (0, 1)-решений неравенства
совпадает с множеством характеристических векторов элементов множества fG, то граф G называется пороговым, а неравенство (1) — разделяющим неравенством.
Например, граф, изображенный на рис. 50.1, является пороговым, 3x1 + 2x2 + x3+2x4≤ 3 — разделяющее нера-
 |
венство. Очевидно, что полный и пустой графы также являются пороговыми.
Отметим некоторые свойства пороговых графов. Очевидно следующее
Утверждение 50.1. Любой порожденный подграф порогового графа также является пороговым.
Лемма 50.2. Графы 2К.2, Р4 и С4 не являются пороговыми.
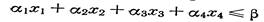 |
В самом деле, изобразим схематично все три рассматриваемых графа на одном рисунке 50.2. Пусть теперь какой-либо из этих графов пороговый и
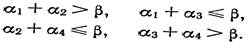 |
— разделяющее неравенство. Тогда
Но последняя система неравенств противоречива. Тем самым лемма доказана.
Непосредственно из предыдущего вытекает
Следствие 50.3. Любой пороговый граф не имеет порожденных подграфов вида 2К2, Р4 и С4.
Обозначим через К ° G и О ° G графы, полученные из графа G присоединением новой доминирующей и, соответственно, изолированной вершины.
Лемма 50.4. Если G — пороговый граф, то оба графа K°GuO°G также являются пороговыми.
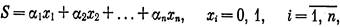 |
Пусть G — пороговый граф порядка п, (1 — разделяющее неравенство. Рассмотрим граф К° G. Пусть а — минимальное число среди коэффициентов ά1, в неравенстве (1); b — минимальное число среди всех таких сумм
что S > β; δ и γ — произвольные числа, удовлетворяющие неравенствам
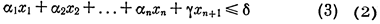 |
(В случае, когда G = On, указанного b не существует и в (2) соответствующее неравенство опускается.) Прямая проверка подтверждает, что неравенство
является разделяющим для графа К° G.
Аналогично, взяв в (3) γ и δ , удовлетворяющие условиям β < δ < b, γ ≤ δ — β , получим разделяющее неравенство для графа О °G.
Как отмечалось выше, некоторые графы являются униграфами, т. е. с точностью до изоморфизма определяются своими степенными последовательностями.
Из того факта, что любые две реализации графической последовательности получаются одна из другой с помощью цепочки переключений (теорема 45.1), вытекает Следствие 50.5. Граф G является униграфом тогда и только тогда, когда для любого переключения s графы G и sG изоморфны.
Ниже доказано, что пороговые графы и только они составляют простейший класс K униграфов — графов, вовсе не допускающих переключений, отличных от тождественного. Непосредственно из определения переключения вытекает следующая характеризация этого класса в терминах запрещенных порожденных подграфов.
Утверждение 50.6. Граф принадлежит классу K тогда и только тогда, когда ни один из трех графов 2К2, Р4 и С4 не является его порожденным подграфом.
Следствие 50.3 означает, что любой пороговый граф принадлежит классу K.
Лемма 50.7. Если G € K, то в графе G есть либо доминирующая, либо изолированная вершина.
Пусть, напротив, G е K и в графе G нет ни доминирующих, ни изолированных вершин, и пусть и — его вершина максимальной степени. Тогда в этом графе существуют две такие вершины v и w, что uv € EG, uw ¢ EG.
Если при этом vw € EG, то, поскольку степень вершин и максимальна, существует четвертая вершина x, смежная с и и не смежная с v (см. рис. 50.3). Порожденный подграф G(u, v, w, х) входит в список подграфов, фрещенных для класса Ж утверждением 50.6 (он совпадает с Р4 или с С4).
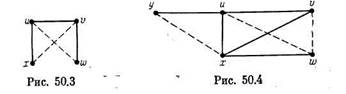 |
Пусть vw ¢ EG. Так как в графе G нет изолированных вершин, то существует четвертая вершина х, смежная c w. Вершины и и v смежны с х, иначе порожденный
граф G(u, и,w,x) имел бы вид, запрещенный утверждением 50.6.. Так как и — вершина максимальной степени, то существует пятая вершина у, смежная с и, но не смежная с х. Подграф G{u,w, х, у) снова запрещенный ис. .50.4).
Полученное противоречие доказывает лемму.
Очевидны следующие два свойства графов из класса K.
1. Порожденный подграф любого графа из класса K также принадлежит этому классу.
2. Если G € K, то оба графа К° G и О °G также принадлежат классу K.
Для п > 2 положим
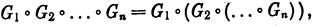 |
где Gn = K1, Gi = К или Gi = 0 ( i = 1, п — 1). Очевидно, что из вышесказанного вытекает следующее
Утверждение 50.8. Класс K есть класс всех графов, имеющих вид
Gi о G2 °... °Gn,
где Gn = K1, п ≥ 1, а для i= 1, п — 1 компоненты Gi независимо друг от друга принимают значения К или О.
Теорема 50.9. Граф является пороговым тогда и только тогда, когда он имеет вид, описанный в утверэкгдении 50.8.
Требуется доказать, что класс пороговых графов совпадает с классом K . Выше отмечалось, что любой пороговый граф принадлежит классу K . С другой стороны,согласно утверждению 50.8 любой граф из класса K можно построить, исходя из одной вершины, присоединяя на каждом шаге к уже полученному графу либо доминирующую, либо изолированную вершину. Одновершинный граф является пороговым. Согласно лемме 50.4 свойство пороговости графа сохраняется при присоединении к графу новой доминирующей или изолированной вершины. Следовательно, любой граф из класса K является пороговым.
Следствие 50.10. Любой пороговый граф является расщепляемым.
 |
Пусть пороговый граф G получается из вершины а в результате присоединения на каждом шаге к уже полученному графу либо доминирующей, либо изолированной
вершины. Отнеся к верхней доле вершину а и все вершины, присоединенные как доминирующие, а к нижней доле — все остальные вершины, получим полярное разбиение множества VG. Следовательно, граф G расщепляем.
Следствие 50.11. Для любого натурального числа п существует ровно 2n-1 попарно неизоморфных пороговых графов порядка п.
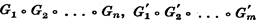 |
Очевидно, что два графа
вида, описанного в утверждении 50.8, изоморфны тогда и только тогда, когда
п = m, Gi = Git i = 1, п — 1.
Каждая из компонент Gi может принимать два значения. Следовательно, число неизоморфных среди таких графов равно 2n-1.
На рис. 50.5 показаны все 8 пороговых графов порядка 4. Из теоремы 50.9 следует, что каждый из них определяется (0, 1)-вектором (α, β, γ).
Непосредственно из теоремы 50.9 вытекает Следствие 50.12. Если G — пороговый граф, то и дополнительный граф G также является пороговым.
Графическая последовательность, имеющая пороговую реализацию, называется пороговой. Все реализации пороговой последовательности изоморфны, поскольку пороговый граф является униграфом. Очевидно, что из теоремы 50.9 вытекает следующий критерий пороговости последовательности целых неотрицательных чисел.
Следствие 50.13. При тг>1 правильная п-последо-вателъность d является пороговой тогда и только тогда, когда верно одно из следующих двух утверждений:
1) d1 = п— 1 и производная последовательность d1 = {d2—i, ..., dn— 1) пороговая;
2) dn = 0 и производная последовательность dn = { d1, d2, ..., dn-1) пороговая.
§ 51. Пороговое разложение графа
Поскольку граф с одним ребром является пороговым, то любой граф G можно представить в виде объединения
G = G1 U G2 U ... U Gt
пороговых графов G, с совпадающими множествами вершин. Назовем такое представление пороговым разложением графа G. Минимальное число t компонент в пороговых разложениях графа G назовем пороговым числом графа G и обозначим через th(G).
Параметр th(G) связан с минимизацией числа линейных неравенств, задающих булеву функцию. Рассмотрим эту связь. Пусть
 |
— система линейных неравенств с вещественными коэффициентами и правыми частями, В — {0, 1}, Вп — множество всех бинарных векторов (х1 ,х2 ,.., хп) длины п. Определим булеву функцию ƒ: Вп->В, положив f (х1 ,х2 ,.., хп) = 0 тогда и только тогда, когда вектор (х1 ,х2 ,.., хп) удовлетворяет системе (1). Будем говорить, что функция f определяется системой неравенств (1). Тем самым множество нулей булевой функции, определяемой системой линейных неравенств, совпадает с множеством (0, 1)-решений этой системы.
Теорема 51.1. Любая булева функция определяется некоторой системой линейных неравенств.
Известно, что всякая булева функция ƒ от п переменных может быть задана своей совершенной дизъюнктивной нормальной формой (совершенной д. н. ф.):
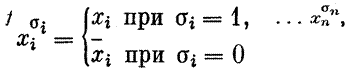 |
где (σ1, σ2, ... , σn) пробегает множество всех единиц функции ƒ,
(см., например, [32]).
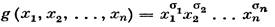 |
Легко видеть, что каждая конъюнкция g вида
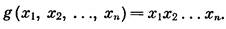 |
определяется одним линейным неравенством. В самом деле, пусть, для определенности,
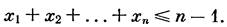 |
Рассмотрим неравенство
Бинарный вектор х = (х1 ,х2 ,.., хп) не удовлетворяет этому неравенству только при условиях
х1= х2 = …= хп =1
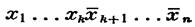 |
Но эти же условия необходимы и достаточны для того, чтобы вектор х был единицей функции ƒ. Аналогично, конъюнкция
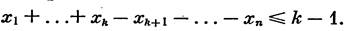 |
определяется неравенством
Итак, каждая элементарная конъюнкция, входящая в совершенную д. н. ф. функции ƒ, определяется одним линейным неравенством. Очевидно, что функция ƒ определяется системой этих неравенств.
Минимальное число t неравенств в системах, задающих функцию ƒ, называется пороговым числом функции ƒ и обозначается через t(f). Если функция ƒ графическая, т. е. ƒ = 0 или ƒ — монотонная булева функция, все нижние единицы которой имеют норму 2, то, как показано в 28, этой функции соответствует граф G t , множество характеристических векторов независимых подмножеств вершин которого совпадает с множеством нулей функции ƒ.
Теорема 51.2. Для любой графической функции f верно равенство
t(f) = th(Gt). (2)
Пусть ƒ — графическая функция,
Gt = Gi U G2 U ... U Gt
 |
пороговое разложение графа Gt. Тогда система fGt всеx независимых подмножеств вершин графа Gt есть пересечение
Аналогичных систем для пороговых графов Ga. Множество характеристических векторов элементов системы fGa совпадает с множеством бинарных решений линейного неравенства, являющегося разделяющим для графа Ga. Из неравенства (3) следует, что множество бинарных решений системы из t таких неравенств есть множество характеристических векторов элементов из fGf, т. е. множество нулей функции f. Следовательно, эта система неравенств задает функцию f, и потому t(f) ≤ t. Итак, t(f) ≤ th(Gi).
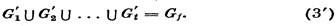 |
Обратно, пусть функция f задается некоторой системой линейных неравенств (1). Следующим образом построим t графов G'h (k = 1, t) : VG'h = {1,2, ...,n}, ij € EG'h тогда и только тогда, когда i ≠ j и αki + αkj > βk. Очевидно , что
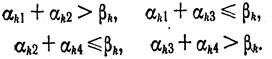 |
Предположим, что какой-либо из графов G'h не является пороговым. Тогда в нем есть порожденный подграф, запрещенный следствием 50.3; пусть это подграф, показаный на рис. 50.2, где пунктирные линии означают отсутствие соответствующих ребер. Из определения графа G'h следует, что
то последняя система неравенств противоречива, следовательно, G'h — пороговый граф. Итак, (3')—пороговое разложение графа Gf. Поэтому th(Gf) ≤ t и, следовательно, th(Gf) ≤ t(f). Равенство (2) доказано.
Вычисление порогового числа произвольного графа G и, тем более, построение соответствующего порогового разложения графа — крайне трудные задачи. Пороговое число можно оценить с помощью числа независимости ao(G), однако последнее так же трудно вычислимо.
 |
Теорема 51.3 (В. Хватал, П. Хаммер, 1977 г.). Для любого непустого графа G порядка п верно неравенство
Пусть S — наибольшее независимое множество вершин графа G%
VG\S = {u1 ,u2, ..., uh}.
 |
Обозначим через Ei множество ребер графа G, инцидентных вершине ui (i = 1, k). Поскольку ребра, входящие в Еi, составляют звезду, являющуюся согласно теореме 50.9 пороговым графом, то и граф Gi = (VG, Еi ) пороговый. Но
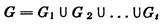 |
Следовательно, (6) — пороговое разложение графа G. Поэтому th(G) ≤ k= п — ao (G), т. е. верно неравенство (4). Пусть теперь в графе G нет треугольников и пусть
— пороговое разложение с минимальным числом компонент. В пороговом графе G< также нет треугольников. Из теоремы 50.9 следует поэтому, что граф Gi является звездой или получается из звезды в результате присоединения изолированных вершин. В любом случае в графе Gi есть вершина ui инцидентная всем его ребрам. Так как U EGi = EG, то множество VG\{ u1 , u2, ..., ut) независимо в графе G. Следовательно, ao(G) ≥ n — th(G), что вместе с неравенством (4) приводит к равенству (5).
Заметим, что равенство (5) может быть верным и для графа с треугольниками. Таков, например, граф на с. 51.1.

|
Поскольку для любого n-вершинного графа G верно равенство ao(G)+ β0(G) = n (теорема 25.5), где βo(G)— число покрытия графа G, то из предыдущей теоремы вытекает
Следствие 51.4. Для любого графа G, не содержащего треугольников, верно равенство th (G)= βo(G).
В частности, любой двудольный граф не содержит треугольников. Кроме того, для двудольного графа G верно равенство (G) = a1(G), где a1(G) — число паросочетания (теорема 32.1). Поэтому из теоремы 51.3 вытекает
Следствие 51.5. Для любого двудольного графа G верно равенство th(G) = a1(G).
Таким образом, в классе двудольных графов параметр (G) вычисляется несложно.
Дата добавления: 2019-07-26; просмотров: 795;
