Критерии графичности последовательности

Как отмечалось выше, графическую последовательность всегда можно считать правильной. Кроме того, в ней должны быть равные члены (если длина ее п > 1), поскольку не существует графа, степени всех вершин которого попарно различны (см. упражнение 11 в гл. I).

Однако указанные условия отнюдь не являются до-статочными для графичности последовательности. Оче-видно, например, что последовательность (3², 1²) не яв-ляется графической, хотя и удовлетворяет упомянутым условиям.

Известно несколько критериев графичности последо-вательности. Одной из важнейших теорем такого рода является критерий Гавела - Хакими, к изложению ко-торого мы приступим.

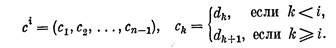Пусть d — правильная n-последовательность, п > 1. зафиксируем индекс i, 1≤ i ≤ п, и через сⁱ обозначим (n-1)-последовательность, которая получается из последовательности d вычеркиванием i-гочлена. Тем самым

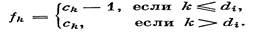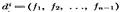Пусть, далее, последовательность получается из последовательности с^г в результате уменьшения на единицу каждого из первых di- членов:

Когда d^l называется производной последовательностью.

Например, если d = (3, 3, 1, 1), то d¹=(2,0,0)=d², d³=(2, 3,1)= d⁴.

Теорема 46.1 (В. Гавел, 1955 г., С. Хакими, 1962 г.). Пусть d — правильная п-последователъностъ, n > 1. Если для какого-либо индекса i, 1≤ i ≤ п, производная последовательность d^l является графической, то и n— графическая последовательность. Если последовательность d графическая, то каждая последовательность

(i=1, n) является графической.

Пусть dⁱ — графическая последовательность, Н — её реализация. Добавив к графу Н новую вершину и соединив ее ребрами с d_{ вершинами наибольших степе-вй, получим реализацию последовательности d. Следоательно, d — графическая последовательность.

Обратно, пусть последовательность d является графической. Согласно лемме 45.2 существует такая реализа-ия G этой последовательности, в которой некоторая вершина v степени d_{ смежна с d_{ вершинами, степени которых наибольшие. Очевидно, что граф G — v является реализацией последовательности dⁱ

Предыдущий критерий вместе с леммой 45.2 подсказывают алгоритм распознавания графичности правильной последовательности и построения одной из ее реализаций. Назовем этот алгоритм l-процедурой. Пусть d — равильная n - последовательность, V — n-элементное множество вершин (будущего графа), каждому элементу v которого приписано неотрицательное целое число d (v)—метка, причем d{v)<n. Пусть, далее, S(v)—подмножество V, составленное из d(v) отличных от вершины v вершин с максимальными .метками (S(v) определено не однозначно). Шаг l-процедуры заключается в следующем:

1) фиксировать произвольную вершину v с положительной меткой (далее эта вершина называется ведущей);

2) фиксировать одно из подмножеств S(v);

3) вершину v соединить ребром с каждой вершиной из S(v);

4) изменить метки вершины v и каждой из вершин и, входящих в S(v), положив d(v):=0, d(u):= d(u)— 1.

Если в результате применения шага l-процедуры какая-либо из меток становится отрицательной, то говорят, что этот шаг проваливается.

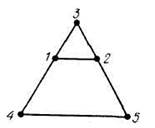l-процедура применяется к правильной n-последовательности d и заключается в последовательном выполнении шагов. Берем V = {1, 2, ..., п} и первоначально

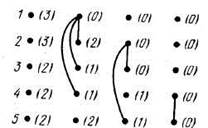
Рис. 46.1

полагаем d(i) = d_u Из леммы 45.2 и критерия 46.1 вытекает, что возможно одно из двух: либо мы приходим к нулевой последовательности меток и одновременно получаем реализацию последовательности d, либо очередной шаг проваливается, т. е. последовательность d не является графической.

На рис. 46.1 Z-процедура демонстрируется на примере последовательности (З², 2³). Каждый столбец на этом рисунке соответствует одному шагу /-процедуры.

Отметим еще один критерий графичности последовательности.

Теорема 46.2 (П. Эрдёш, Т. Галлаи, 1960 г.). Правильная п-последователъностъ d является графической тогда и только тогда, когда для каждого к = 1,п-1 верно

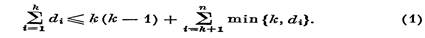неравенство

Необходимость неравенства (1) проверяется легко.

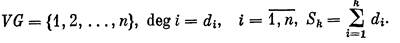Пусть G — реализация последовательности d,

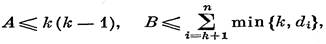Разобьем сумму S_k на две части: S_k = A + В, где А — сумма степеней вершин порожденного подграфа G(l, 2, ..., k), а В — вклад, вносимый в сумму S_h ребрами вида ij, где i ≤ k, j > k:, Очевидно, что

откуда и вытекает неравенство (1).

Приведем доказательство достаточности условий теоремы, принадлежащее С. А. Чоудаму (1986 г.). Пусть d — правильная n-последовательность, причем неравенство (1) верно для каждого k = 1, п— 1. Если d_i = r (i—1, п), то хотя бы одно из чисел r и n четное, поскольку сумма членов последовательности d — четное число. Кроме того, r≤п—1. При этих условиях существует п -вершинный регулярный граф степени r (утверждение 7.1). Стало быть, d — графическая последовательность.

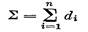Пусть теперь среди членов di последовательности d есть различные. Не ограничивая общности, рассмотрим случай, когда d_n ≠ 0. Воспользуемся индукцией по сумме членов последовательности d. При Σ = 2 условиям теоремы удовлетворяет только одна n-последовательность (1, 1, 0, ..., 0); эта последовательность, очевидно, графическая. Возьмем теперь Σ > 2 и предположим, что условия теоремы достаточны для графичности любой правильной n-последовательности с меньшей чем Σ суммой членов. Пусть t = min{i: d_i> d_i₊₁). Тогда 1 ≤ t ≤n - 1. Положим

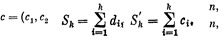и докажем, что последовательность с также удовлетворяет условиям теоремы. Пусть

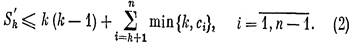Заметим, что S'_k= S_k (k —1,t — l). Нужно доказать неравенства

Это совсем просто при k ≥ t. Имеем

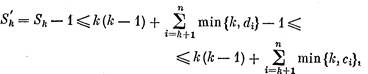и неравенство (2) верно.

Пусть теперь к ≤ t— 1. В этой ситуации

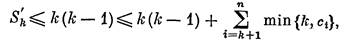Если, к тому же, d_h<k— 1, то из равенств (3) непосредственно вытекает

т. е. неравенство (2) верно.

Далее отдельно рассмотрим две возможности: 1) d_k = k, 2) d_k ≥ k + l.

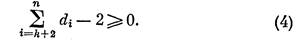1) Заметим, что в рассматриваемом случае

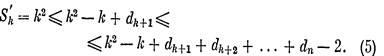Это очевидно при k + 2 < n— 1. Если же k + 2 = п, то t = n— 1 и, следовательно d = ((n - 2)ⁿ^-1, d_n). Далее, имеем Σ = (п — 2) (n — 1) + d_n. Так как Σ — четное число и d_n > 0, то d_n ≥ 2, откуда и следует неравенство (4). Согласно (3) и (4)

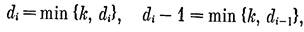Для i > k имеем

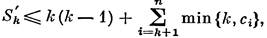поэтому из (5) следует, что

т. е. неравенство (2) верно.

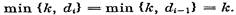2) Если d_n ≥ k + 1, то

Поэтому

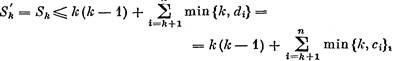и неравенство (2) верно.

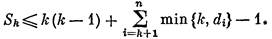Пусть теперь d_n < k + 1. В этом случае верно неравенство

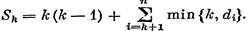Действительно, если, напротив, (6) неверно, то

Положив r = min (i: d_t₊_i₊₁< k) и учитывая (3), получим

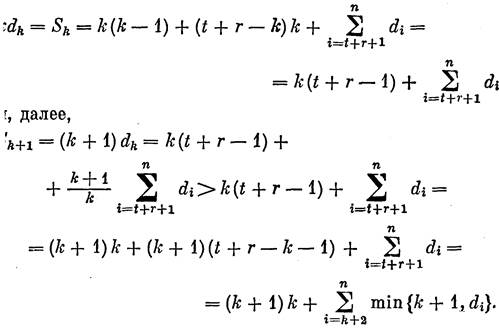Последнее противоречит тому, что последовательность d удовлетворяет неравенствам (1). Неравенство (6) доказано. С учетом (6) и (3) получаем

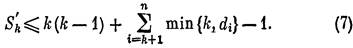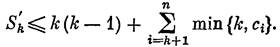В рассматриваемом случае t ≥ k + 1, d_t = d_k ≥ k + 1, min {k , d_t}=min {k, c_t}=k, min {k, c_n} = c_n = d_n — 1, min { k , d_n} = d_n , поэтому из (7) вытекает

Тем самым доказано, что в любой ситуации последовательность с удовлетворяет условиям теоремы. Так как сумма членов этой последовательности равна Σ — 2, то она графическая по индуктивному предположению. Возьмем произвольную реализацию G последовательности с. Пусть а, b €VG, deg a = c_i, deg b = с_п. Если вершины а и b не смежны, то граф G + аb является реализацией последовательности d и, следовательно, d — графическая последовательность.

Пусть аb € EG. Так как deg а — d_t — 1 ≤ п — 2, то существует вершина е € VG, не смежная с а. Но deg e ≥ deg b , поэтому существует вершина f € VG, смежная с е и не смежная с b. Итак, граф G допускает переключение s = (ab, ef). Граф sG = G — ab — ef + ae + bf также служит реализацией последовательности с, причем в нем вершины а и b не смежны. Но тогда, как доказано выше, последовательность d является графической.

При тестировании последовательности с помощью критерия Эрдёша — Галлаи нет необходимости проверять все п— 1 неравенств (1). Пусть d — правильная n-последовательность, k(d)= max { i : di ≥ i). Тогда верно следующее

Утверждение 46.3. Если последовательность d удовлетворяет каждому из неравенств (1) при k = 1, k(d), то она удовлетворяет и каждому из оставшихся неравенств (1).

Доказательство опускается.

Дата добавления: 2019-07-26; просмотров: 713;